1.2 Vocab Linear Systems and Matrices

Augmented matrix

A matrix that contains all of the coefficients of a linear system, including the constant terms

Echelon form

A linear system satisfying the following conditions: Every variable is the leading variable of at most one equation; the system is organized in a descending “stair step” pattern so that the index of the leading variables increases from the top to bottom; and every equation has a leading variable. Such a system is called an echelon system

Elementary (equation) operations

Three operations that can be performed on a linear system that do not change the set of solutions, so they yield an equivalent system.

(1) interchanging two equations

2) multiplying an equation by a nonzero constant

3) adding a multiple of one equation to another.

Elementary row operations

Three row operations that can be performed on an augmented matrix that do not change the set of solutions to the corresponding linear system. They are (1) interchanging two rows, (2) multiplying a row by a nonzero constant, and (3) adding a multiple of one row to another

equivalent matrices

2 matrices are equivalent if one can be transformed into the other through a sequence of elementary row operations. If the matrices in question are augmented matrices, then the corresponding linear systems have the same set of solutions

Equivalent systems

2 linear systems are equivalent if they have the same set of solutions

Gauss–Jordan elimination

An algorithm that extends Gaussian elimination, applying row operations in a manner that will transform a matrix to reduced echelon form

Gaussian elimination

An algorithm for applying row operations in a manner that will transform a matrix to echelon form

Homogeneous equation

Eq in the form: they always have a solution

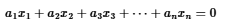
Leading term

In a matrix, the leading term for a row is the leftmost nonzero entry in that row. A row of zeros has no leading term

Matrix

A rectangular table of numbers, upon which various algebraic operations are defined and can be performed. The plural of matrix is matrices

Nontrivial solution

A solution to a homogeneous linear equation (or homogeneous linear system) where some of the variables are nonzero. Although all homogeneous linear equations (systems) have the trivial solution, not all have nontrivial solutions.

Pivot columns

The columns containing pivot positions for a matrix in echelon form

Pivot positions

For a matrix in echelon form, the pivot positions are the locations of the leading terms

Pivot rows

The rows containing pivot positions for a matrix in echelon form

Reduced echelon form

Also called row reduced echelon form, a matrix in this form is in echelon form and each pivot column consists entirely of zeros except for in the pivot position, which contains a 1.

Trivial solution

The solution to a homogeneous linear equation (or homogeneous linear system) where all variables are set equal to zero

Zero column

A matrix column consisting entirely of zeros

Zero row

A matrix row consisting entirely of zeros