Special Center and Segments - Math Unit 8
1/11
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
12 Terms
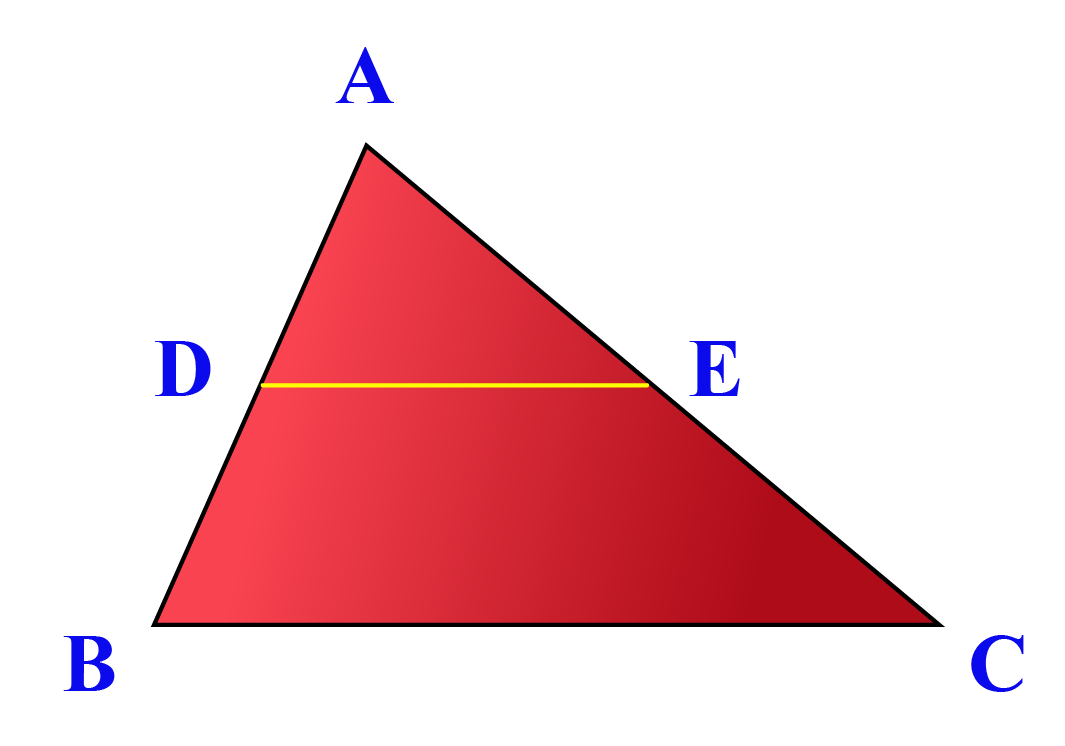
Midsegment
A segment that joins the MIDPOINTS of two sides of a triangle.
Perpendicular bisector
A line, segment, or ray that divides a segment into two EQUAL parts and is PERPENDICULAR to the segment.

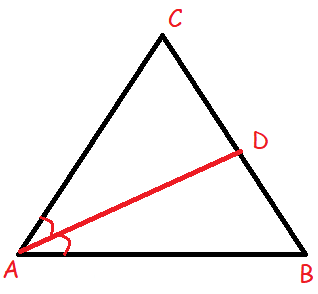
Angle bisector
A line, segment, or ray that divides an angle into two EQUAL parts.
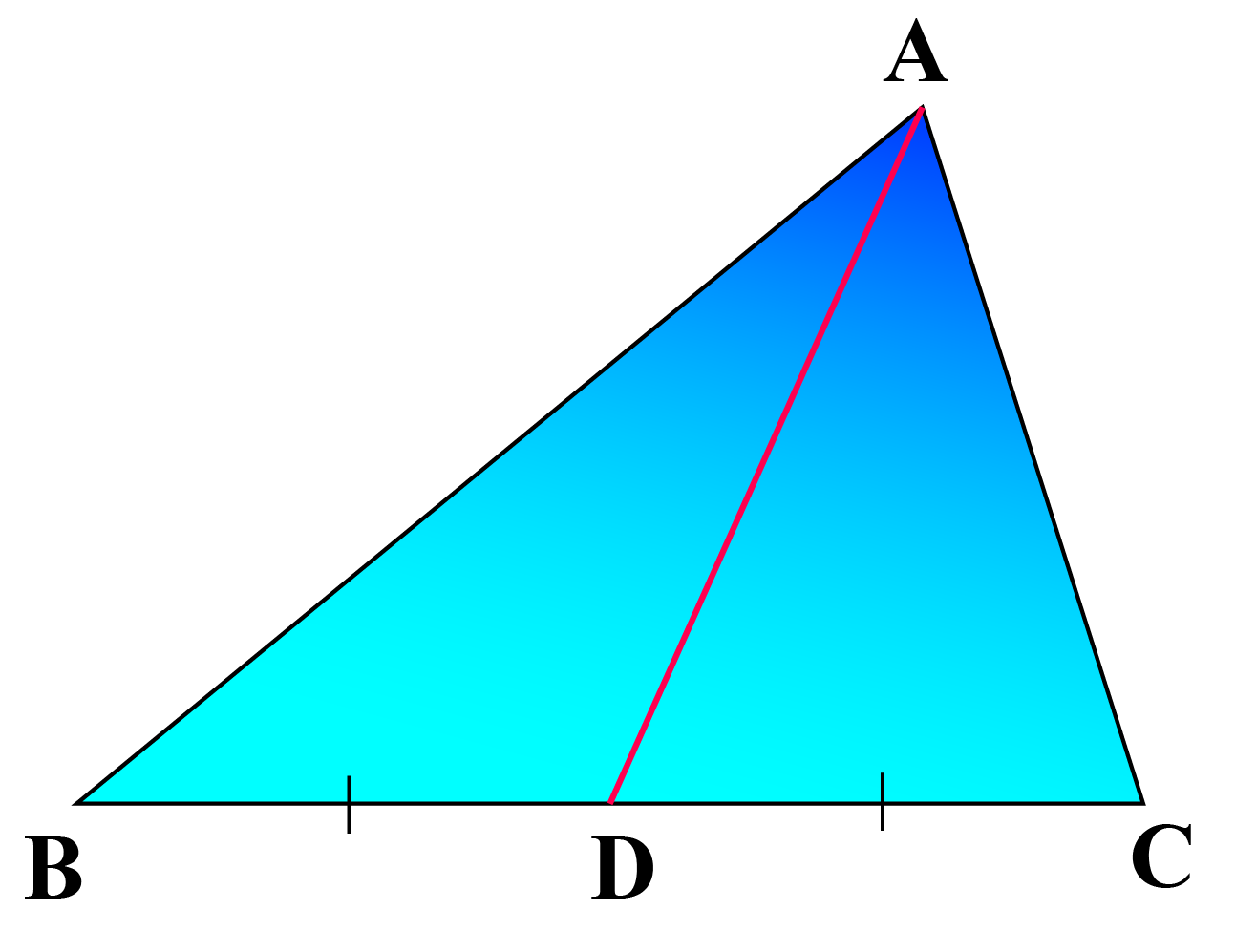
Median
A segment that connects a VERTEX of a triangle to the MIDPOINT of the opposite side.
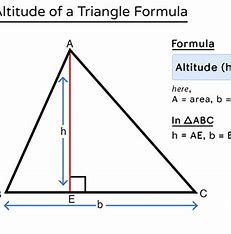
Altitude
A segment that connects a VERTEX of a triangle to the line on the opposite side and is PERPENDICULAR to that side.
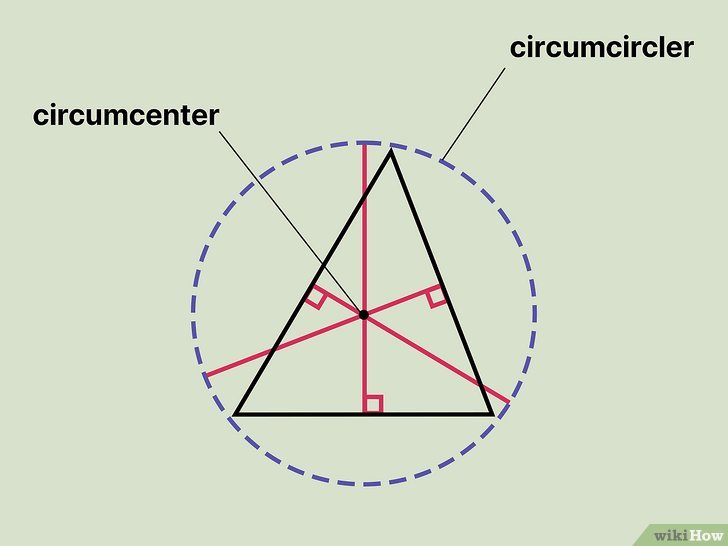
Circumcenter
The point at which the three perpendicular bisectors intersect in a triangle.
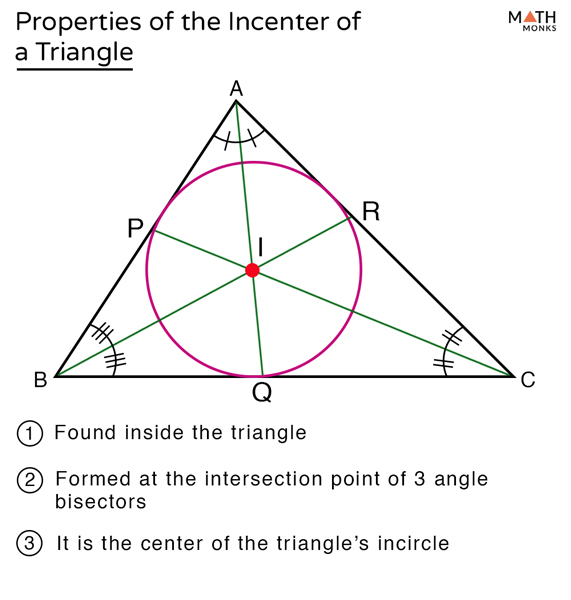
Incenter
The point at which three angle bisectors intersect in a triangle.
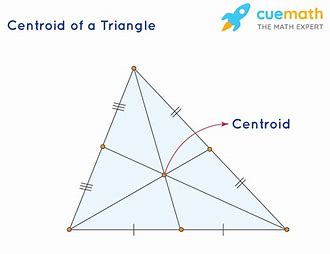
Centroid
The point at which the three medians intersect in a triangle.
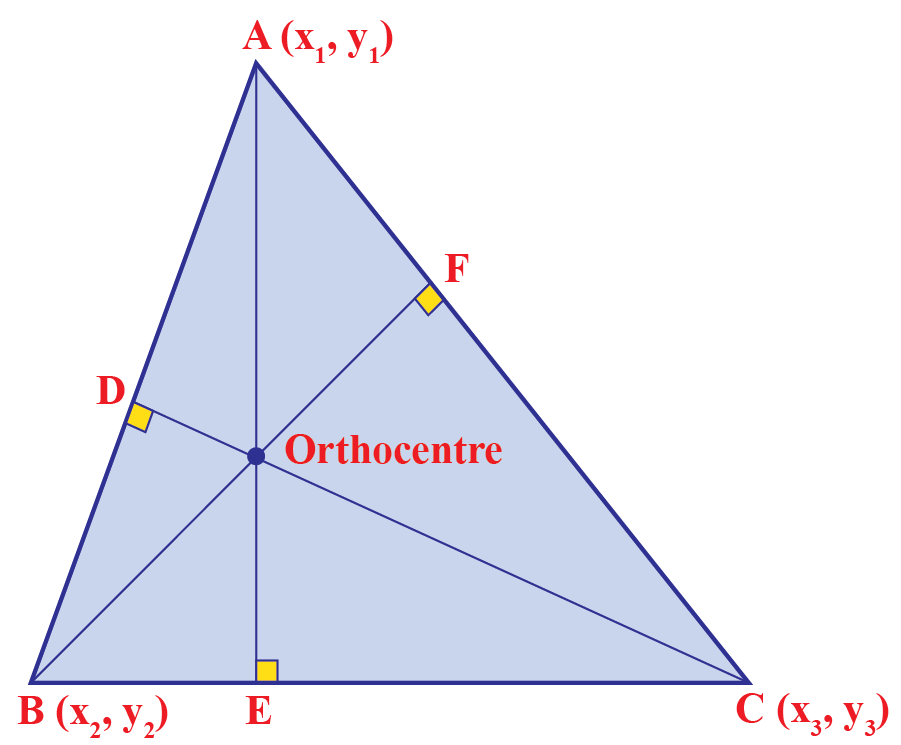
Orthocenter
The point at which the three altitudes intersect in a triangle.
Orthocenter of an acute triangle
Located inside the triangle.
Orthocenter of a right triangle
Located in the vertex of the right angle.
Orthocenter of an obtuse triangle
Located outside of the triangle.