Lecture 19 - Potential Energy and Conservation of Mechanical Energy

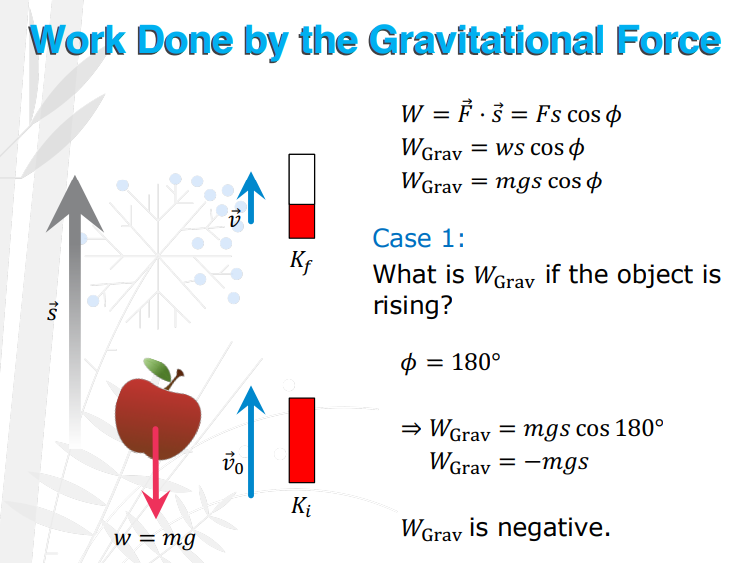
θ = 180° or negative mgy

What is W_grav if the object is rising?

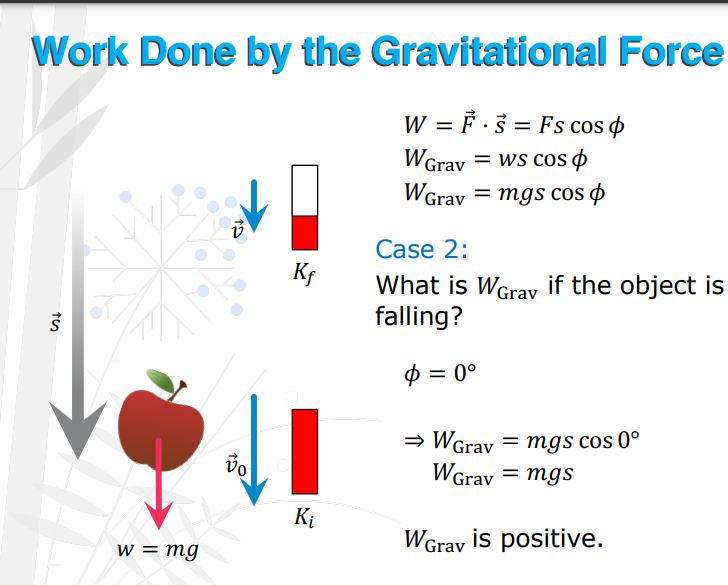
θ = 0° or positive mgy

What is W_grav if the object is falling?

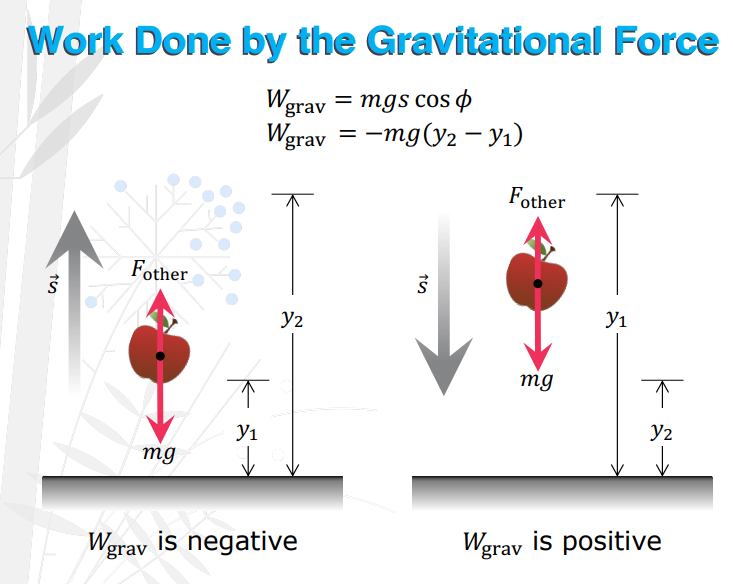
W_grav = -mg(y₂-y₁)

W_grav = Formula for y₂ and y₁ is ______

W_grav = mgscosθ

height dependent

Placing an object at a higher position gives it a “potential” for gravity to do work on it. Gravitational potential energy (GPE) is _____________ where the upwards direction is taken to be positive (+).

W_grav = −ΔU_grav

Gravitational potential energy is related to the work done.

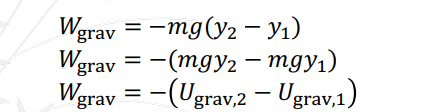
K_{2 ⁺} U_{grav2 ⁼} K_{1 +} U_grav1

Gravitational potential energy is related to the work done. We can relate the work-kinetic energy theorem. K_2^-K_{1 ⁼} U_grav1- U_grav2

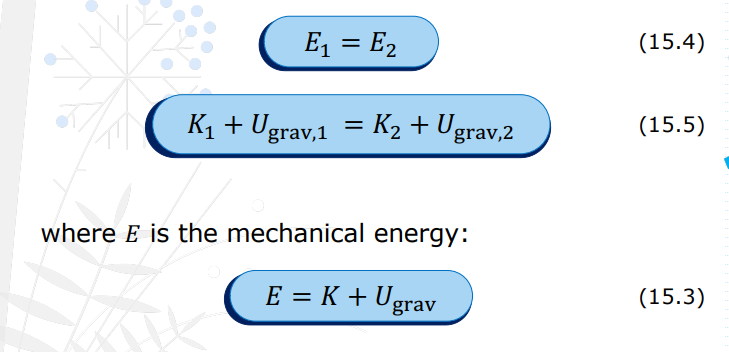
E = K + U_grav

Total mechanical energy of the system (object and earth) is given by the formula _________ which is also a conserved quantity when ONLY gravity does the work.

Conserved Force

When only the force of gravity does work, the total mechanical energy is constant—that is, it is a ____________.

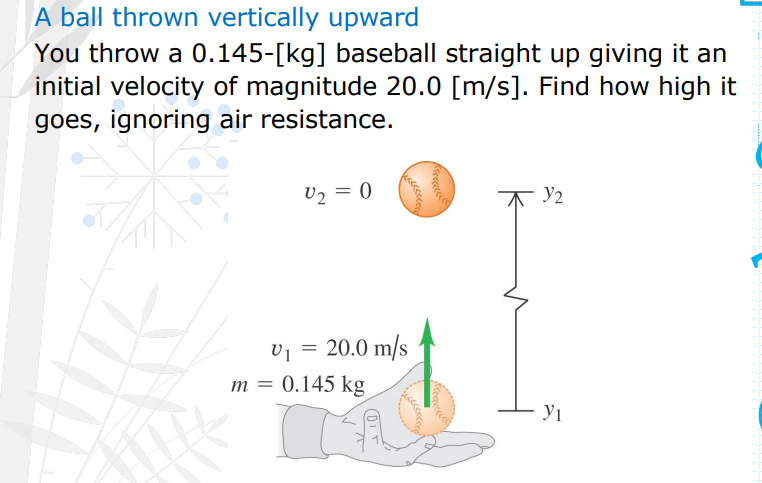
First, gravity is the only force acting on the ball, use the conservation of energy. Derive the equation for y₂ where origin is 0, and final velocity is 0. Even if there was an initial height, simply get the height difference.

Steps in solving this problem.

ΔU_{grav ⁼} ΔU_grav

Gravitational Potential Energy: Curved Path, the work is unaffected by horizontal motion that may occur as ____________.

At a set height h, the E = K + Ugrav remains the same.

Projectile Motion For the same initial speed and initial height, the speed of a projectile at a given elevation h is always the same, neglecting air resistance.

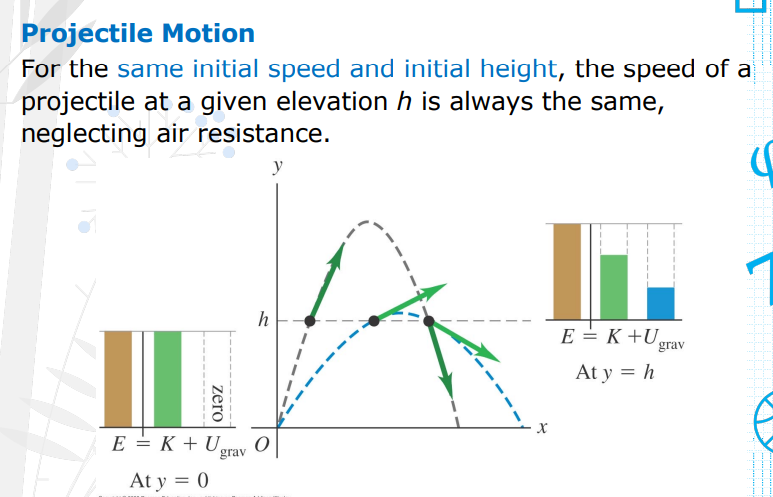
Use Conservation of Mechanical Energy, the only given that will matter is V1, Y1, and Y2.

Standing near the edge of the roof of a 12[m] building, you kick a ball with an initial speed of vi = 16 [m/s] at an angle of θ = 60°. above the horizontal. Neglecting effects due to air resistance, find its speed just before it hits the ground.

Conservative Forces

These forces point toward the direction of lower potential energy.

Conservative Forces

The work done is reversible.

Conservative Forces

The work done just depends on the final and initial values of the potential energy. (State Function)

Conservative Forces

The work done is path independent.

Non-conservative Forces

Total mechanical energy is not conserved.

Non-conservative Forces

Work done by non conservative force changes the total mechanical energy.

Non-conservative Forces

• Frictional force Ø

• Force due to the engine

• Force that we applied, etc.