ECON 491 Lecture 14: Shrinkage/Regularization

Shrinkage Methods (also known as Regularization)

Use all p predictors to fit a model. However, the estimated coefficients are shrunken (or constrained or regularized) towards zero relative the least squares estimates.

**With some shrinkage methods, some of the coefficients may be estimated to be exactly zero; shrinkage methods can perform variable selection

Two popular shrinkage techniques:

→ Ridge Regression

→ Lasso Regression

Ridge Regression

→ Ridge regression minimizes both RSS and the term λ (Sigma) p^_j=1 β² _j (*This term is called shrinkage penalty)

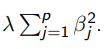
What is the shrinkage penalty?

It gets small when β1, . . . , βp are close to zero—it forces estimates closer to zero.

→ The tuning parameter λ ≥ 0 controls the relative impact of the RSS and the shrinkage penalty.

→ When λ = 0, the penalty has no effect, the ridge regression will produce the least squares estimates.

→ When λ → ∞, the penalty grows and the ridge regression will produce estimates closer to zero.

—CV is used to select a good value for λ.

***Note: The shrinkage penalty does not apply to intercept β0; it applies only to β1, . . . , βp.

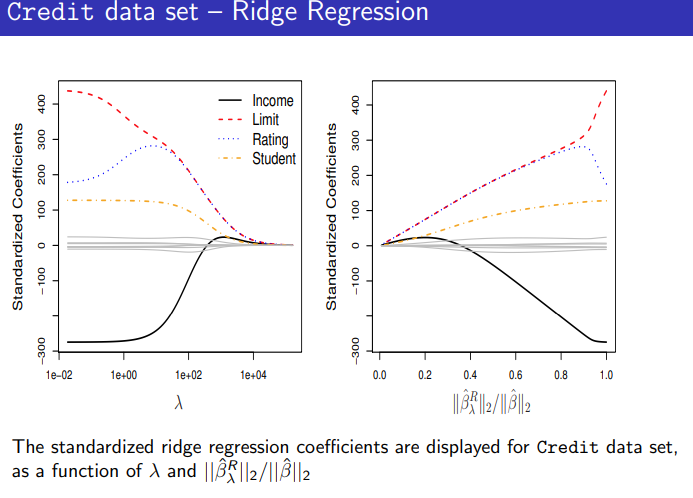
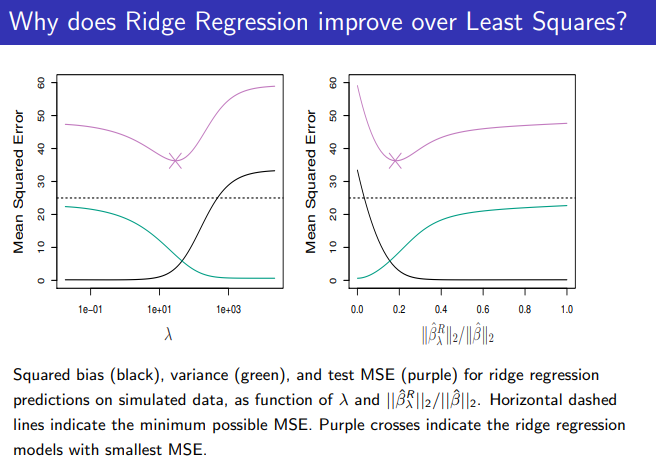
(ONE SIDED)

The LASSO (Least Absolute Shrinkage and Selection Operator)

→ Ridge regression will include all p predictors in the final model which is a disadvantage for interpretation. The Lasso overcomes this problem

→As with ridge regression, the lasso shrinks the coefficient estimates towards zero; —However in the case of the Lasso, the L1 penalty has the effect of forcing some of the coefficient estimates to be exactly equal to zero when the tuning parameter λ is sufficiently large.

→ Much like best subset selection, the lasso performs variable selection

→ As in ridge regression, selecting a good value of λ for the lasso is critical; CV again is the method of choice.

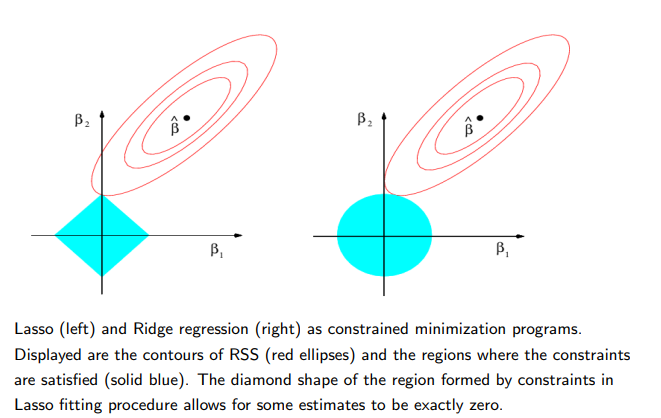
Comparing the Lasso and the Ridge regression (ONE SIDED)

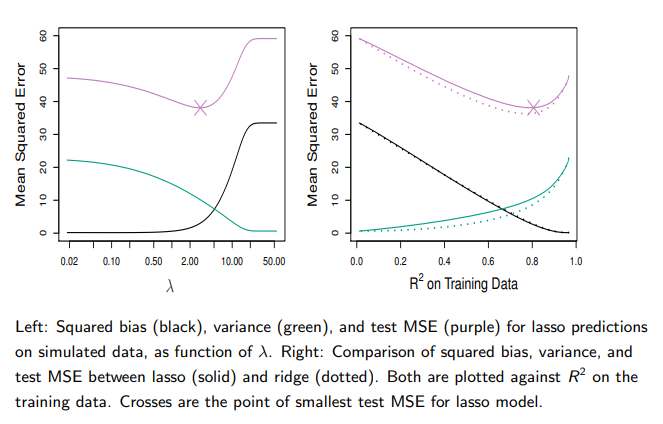
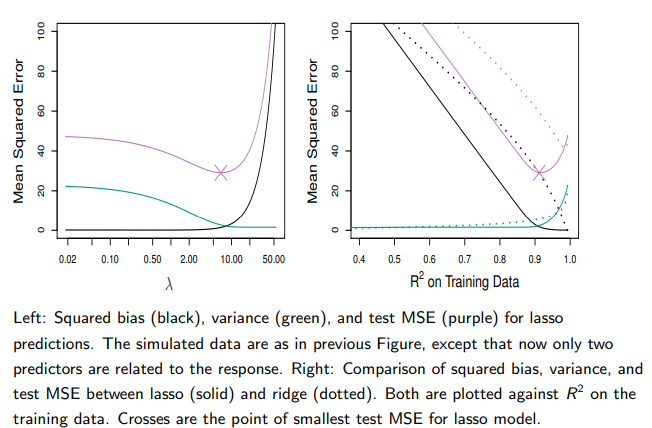
Comparing the Lasso and the Ridge Regression C’td

→ These two examples illustrate that neither ridge nor lasso will universally dominate the other

→ In general, one might expect the lasso to perform better when the response is a function of only a relatively small number of predictors

→ However, the number of predictors that is related to the response is never known a priori for real data sets

→ A technique such as cross-validation can be used in order to determine which approach is better on a particular data set

Selecting the Tuning Parameter λ for Ridge Regression and Lasso

→ CV is used

→ We choose a grid of λ values, and compute the CV error rate for each value of λ.

→ Then select the tuning parameter value for which the CV error is smallest

→ Finally, the model is re-fit using all of the available observations and the selected value of the tuning parameter.