Statistics Exam 4 Study Guide

Gold Standard

Most accurate test available available to diagnose a disease (used as a benchmark to compare new tests)

Test Variable

Screening Variable (test result: positive or negative)

State Variable

Disease State (does the patient have/doesn’t have disease) or Gold Standard

Sensitivity

True Positive (accurately identifies the presence of a disease)

False Positive

Test indicates a disease is present in that patient, when it actually is not present 

Specificity

True Negative (accurately indicates that the disease is not present)

False Negative

Test indicates that the disease is not present in the patient, when it actually is present

Highly Sensitive Test

Very good at identifying the patient with a disease (has a low percentage of false negatives)

Low Sensitivity Test

Limited in identifying the patient with a disease (has a high percentage of false negatives)

If a sensitive test has negative results, the patient is…

Less likely to have the disease

High Specific Test

Very good at identifying patients without a disease (low percentage of false positives)

Low Specific Test

Limited in identifying patients without a disease (high percentage of false positive)

If a specific test has positive results, the patient is…

More likely to have the disease

A

True Positive (# of people who have the disease and the test is positive) 

B

False Positive (# of people who don’t have the disease and the test is positive)

C

False Negative (# of people who have the disease and the test is negative)

D

True Negative (# of people who don’t have the disease and the test is negative)

Sensitivity

Probability of having the disease (true positive rate)

Sensitivity Formula

A ÷ (A + C)

Specificity

Probability of the absence of disease (true negative)

Specificity Calculation

D ÷ (B + D)

False Positive Calculation

Probability of no disease but having a positive test result (false positive rate)

False Positive Calculation Formula

B ÷ (B + D)

False Negative Calculation

Probability of having the disease but having negative test

False Negative Calculation Formula

C ÷ (C + A)

Likelihood Ratios

Calculated using sensitivity and specificity to determine the likelihood that a positive test result is a true positive and a negative test result is a true negative

Positive Likelihood Ratio

Ratio of the true positive results to false positive results 

Positive Likelihood Ratio Formula

Sensitivity ÷ (1 - Specificity)

Negative Likelihood Ratio Formula

(1 - Sensitivity) ÷ Specificity

Negative Likelihood Ratio

Ratio of true negative results to false negative results

Likelihood Ratio > 1.0

Increased Likelihood of Disease

Likelihood Ratio < 1.0

Decreased Likelihood of Disease

Very High Likelihood Ratio (>10)

“Rule In” → Indicate that the patient has the disease

Very Low Likelihood Ratio (<0.1)

“Rule Out” → Chance that the patient has the disease extremely reduce

Positive Predictive Value (PPV)

Tells you what the probability is that a subject actually has disease given a positive test result

What is Positive Predictive Value (PPV) dependent upon?

Prevalence of Illness + Sensitivity + Specificity

Positive Predictive Value (PPV) Formula

True Positives (A) ÷ Total # Who Tested Positive (A + B)

Prevalence Formula

(A + C) ÷ (A + B + C + D)

Negative Predictive Value (NPV)

If the subject screens negative, this tells you the probability that the patient really doesn’t have the disease

Negative Predictive Value (NPV) Formula

(D) ÷ (C + D)

Efficiency

Measure of the agreement between the screening test and the actual clinical diagnosis

Efficiency Formula

((A + D) ÷ (A + B + C + D)) x 100

Cohort Study

Follows a group of people overtime to see who develops a disease (starts with expose, looks for outcome)

Case-Control Study

Starts with people who have the disease (cases) and compares them to people without it (controls), looks backward to see exposure history

Cross-Sectional Study

Measures exposure and outcome at the same time, snapshot of a population

Relative Risk/Risk Ratio Formula

(A ÷ A + B) ÷ (C ÷ C + D)

RR < 1 

The group that was exposed had fewer cases develop than the group that was not exposed (exposure may be a protective factor)

RR = 1

No association between the exposure and the illness

RR > 1

Group that was exposed has a higher incidence rate than the group that was not (exposure may be a risk factor)

P

Value of the associate chi-square indicates whether or not our RR value is statistically significant

Attack Rates

Used to determine the origin of an outbreak (specifically foodborne pathogens like listeria)

Attack Rates Formula

# of sick ÷ # of exposed

Odds Ratio

Obtains an indication of association when IV/DV are dichotomous (ratio of odds of an event occuring in one group to the odds of it occurring in another group)

What type of research design does Odds Ratio utlize?

Randomized Experimental, Quasi, Comparative, and Associational 

In Odds Ratio, what must the dependent variable be?

Dichotomous

Odds Ratio Assumptions

No Repeated Measures and Dichotomous Variables

Odds Ratio Formula

AD / BC

Converting OR → Natural Log

Ln(OR)

Standard Error of Ln(OR) Formula

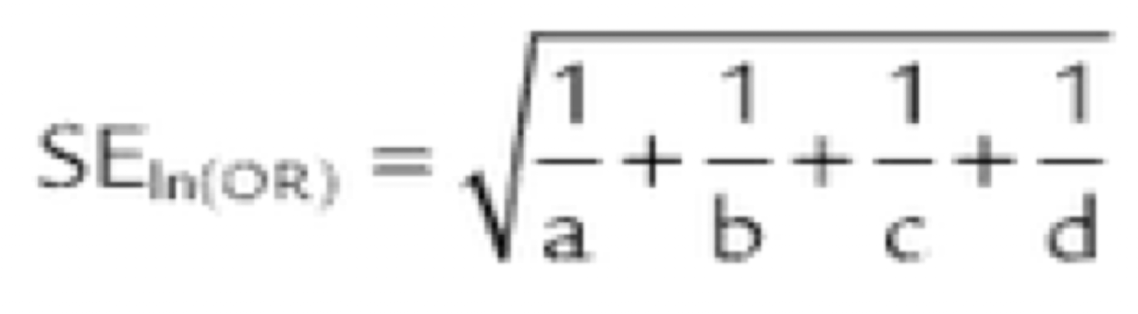
95% Confidence Interval Formula

Ln(OR) ± SE(t)

Upper Limit and Lower Limit of CI Formula

E^{Lower Limit of CI} 

E^{Upper Limit of CI}

OR of = 1.0

No Affect/Relationship

OR of > 1.0

Higher Odds

ANOVA

Examines differences in 3+ groups with repeated measures

Calculated F-Ratio (ANOVA)

Indicates the extent to which group means differ taking into account the variability within the groups

Does the result of an ANOVA test tell us WHERE the difference is or IF there is a difference?

Tells us IF there is a difference

P Value > 0.05 

Insignificant 

If the results are insignificant, what does the researcher do to the null hypothesis: ACCEPT/DENY?

Accepts Null Hypothesis

One-Way ANOVA (Simplest)

1 Independent Variable, 1 Dependent Variable

Repeated ANOVA

Same variable(s) are repeatedly measured over time (determines the change that occurs in the dependent variable with exposure to independent variable) 

ANOVA Assumptions

1. Randomly Sampled + Normally Distributed

2. Mutually Exclusive

3. Equal Variance (Homogeneity)

4. Indepdent Observations

5. DV = Interval/Ratio

Statistic for ANOVA

F

Group Degrees of Freedom (ANOVA)

(# of Groups - 1)

Error Degrees of Freedom (ANOVA)

(# of Participants - # of Groups)

What does P indicate in an ANOVA?

Significance of F-Ratio

Post Hoc Analyses

Developed to determine WHERE the differences lie (example: using a experimental, placebo, and comparison group)

What happens to the alpha level in a post hoc analyses when trying to locate the statistically significant difference?

Reduces/decreases in proportion to the number of additional tests required

As the alpha value level is decreased, reaching the level of significance becomes

Increasingly more difficult

Newman-Keuls

Compares ALL possible pairs of means and is the most liberal (alpha value is not as severely decreased)

Tukey HSD

Computes 1 value with which all means within the data set are compared: requires approximately equal sample sizes in each group (more stringent than Newman)

Dunnett

Requires a control group: the experimental groups are compared with the control group without a decrease in alpha

ANOVA Research Designs

1. Randomized Experimental

2. Quasi-Experimental

3. Comparative Design

Independent Variable in ANOVA

Active or Attributional

ANOVA (F) Formula

F = (Variance Between Groups) ÷ (Variance Within Groups)

What does the between groups variance represent?

Difference between the groups/conditions being compared

What does the within groups variance represent?

Differences among/within each group’s data

Pearson Chi-Square

Inferential statistical test to examine differences among groups with variables measure at the nominal level 

Pearson Chi-Square Statistic 

X²

Pearson-Chi Square Assumptions

Nominal level, adequate sample size, independent observations

What does Pearson-Chi Square compare?

Compares the frequencies that are observed with the frequencies that are expected (Calculated X² values are compared with the critical X² values)

If the result is greater than or equal to the value in the table… (Pearson-Chi Square)

Significant differences exist and thus the null hypothesis is rejected

Pearson Chi-Square Degrees of Freedom

(Rows - 1) (Columns - 1)
Example: In a 2×2 table → (2 - 1) (2 - 1) = 1

Pearson Chi-Square Research Design

Randomized experimental, quasi-experimental, comparative design

Pearson Chi-Square Variables

Active and/or Attributional

One Way X²

Statistic that only compares different levels of 1 variable only 

Two Way X²

Statistic that tests whether proportions in levels of 1 nominal variable are significantly different from proportions of the second nominal variable

What analysis determines the location of the difference?

Post Hoc Analysis

What is the weaker statistical test used? (The results are only reported if statistically significant results were found)

Pearson Chi Square (X²)

Pearson Chi-Square Requirements

1 data entry made for each subject, nominal level, mutually exclusive and exhaustive, sensitive to small sample sizes and other tests

Alternative to Pearson’s R

Spearman Rank