CHapitre 6 : Les 6 sigmas

I. Introduction

I. Introduction

Qu’est-ce que la méthode des 6 sigmas ?

• C’est une méthode d’amélioration des processus

• Vise à réduire la variabilité responsable des dysfonctionnements et de la non-qualité

Que représente le sigma ?

• Un indicateur de performance

• Sert à faire du benchmarking entre processus

• Repose sur le concept de « défauts par million »

Que signifie un « defect » dans le cadre des 6 sigmas ?

• Un dosage, un produit, une action hors de l’objectif fixé est considéré comme un defect

• Plus il y a de defects, plus le niveau sigma est bas

Que signifie un processus « 6 sigmas » ?

• C’est un processus hautement performant

• Ne génère que 3 erreurs pour 1 000 000 d’éléments produits

Donne un exemple de correspondance entre erreurs et niveau sigma.

4 sigmas : 6 210 erreurs par million

Donne des exemples de benchmarking avec la méthode sigma.

• Bagages perdus par million de bagages traités dans un aéroport

• Incidents par million de décollages/atterrissages

• Contaminations HIV par million de transfusions sanguines

• Erreurs de délivrance par million d’ordonnances délivrées

II. Exemple : application

II. Exemple : application

Exemple du golf : comment illustre-t-on le concept de sigma ?

• Parcours par 4, objectif : envoyer la balle entre 150 et 250 yards

Que montre un joueur débutant ?

• Balle :

  • Avant 150 yards → échec

  • Entre 150 et 250 yards → réussite

  • Après 250 yards → échec

• 30 % des coups dans la zone cible → Processus 1 sigma

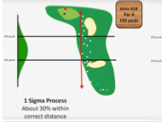
Que montre un joueur un peu expérimenté ?

• 70 % des coups dans la zone cible

• Correspond à un processus 2 sigmas

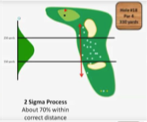
Que montre un joueur de niveau supérieur ?

• 93 % des coups entre 150 et 250 yards

• Processus 3 sigmas

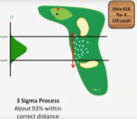
Que montre un joueur encore plus performant ?

• 99 % des coups dans la zone cible

• Processus 4 sigmas

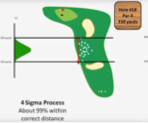
Que montre un joueur quasi parfait ?

• 99,9 % des coups dans la cible

• Processus 5 sigmas

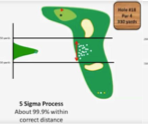
Que représente le processus 6 sigmas au golf ?

• 99,9997 % des coups dans la zone cible

• Soit seulement 3 erreurs sur 1 000 000 coups

• La précision est maximale

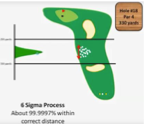
Quelle est l’idée générale du 6 sigmas ?

• Réduire la variabilité au minimum

• Obtenir un niveau de qualité exceptionnellement élevé

III. Calcul du sigma pour évaluer la performance des dosages du laboratoire (et les comparer à d’autres processus !)

III. Calcul du sigma pour évaluer la performance des dosages du laboratoire (et les comparer à d’autres processus !)

Comment calcule-t-on le sigma d’une méthode de dosage au laboratoire ?

Sur quoi repose le calcul du sigma ?

Le sigma est-il universel pour un dosage donné ?

IV. Exemple pratique

IV. Exemple pratique

Sur base de ces données :

• CV analytique (contrôles internes) : 1,32 %

• Biais analytique (contrôle externe) : –2,63 %

• CVI du glucose : 6,5 %

• CVG du glucose : 7,7 %

Calcules de l’erreur totale :

• CV désirable : 0,5 × 6,5 = 3,3 %

• Biais désirable : 0,25 × √(6,5² + 7,7²) = 2,5 %

• Erreur totale désirable :

  TE=1,65×3,3+2,5=7,9

Sur base de ces données :

• CV analytique (contrôles internes) : 1,32 %

• Biais analytique (contrôle externe) : –2,63 %

• CVI du glucose : 6,5 %

• CVG du glucose : 7,7 %

Calcul le sigma du glucose :

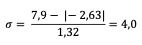
Interprétation du sigma pour le glucose :

• Performance = 4 sigmas

• Cela correspond à 99,38 % des dosages corrects

• Soit environ 6 210 erreurs pour 1 000 000 de dosages

Sur base de ces données :

• CV analytique (contrôles internes) : 1,2 %

• Biais analytique (contrôle externe) : –1,75 %

• CVI du calcium : 2,1 %

• CVG du calcium : 2,5 %

Calcul l’erreur totale du calcium :

• CV désirable : 0,5 × 2,1 = 1,1 %

• Biais désirable : 0,25 × √(2,1² + 2,5²) = 0,8 %

• Erreur totale désirable :

  TE=1,65×1,1+0,8=2,6

Sur base de ces données :

• CV analytique (contrôles internes) : 1,2 %

• Biais analytique (contrôle externe) : –1,75 %

• CVI du calcium : 2,1 %

• CVG du calcium : 2,5 %

Calcul le sigma du calcium :

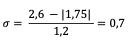
Interprétation du sigma pour le calcium

• Performance ≈ 1 sigma → très faible

• Malgré un biais et un CV faibles, le calcium est fortement régulé biologiquement → la variabilité biologique est trop faible pour le niveau de précision de la méthode

Que faire pour le calcium ?

• Utiliser plutôt l’erreur totale minimale que l’erreur totale désirable

• Reconnaître qu’il est impossible d’atteindre 6 sigmas pour le calcium avec les outils actuels

Sur base de ces données :

• CV analytique (contrôles internes) : 1,8 %

• Biais analytique : 0,9 %

• CVI (TSH) : 29,3 %

• CVG (TSH) : 48,4 %

Calcul l’erreur totale pour la TSH :

• CV désirable : 0,5 × 29,3 = 14,65 %

• Biais désirable : 0,25 × √(29,3² + 48,4²) = 14,14 %

• Erreur totale désirable :

  TE=1,65×14,65+14,14= 38,3 %

Sur base de ces données :

• CV analytique (contrôles internes) : 1,8 %

• Biais analytique : 0,9 %

• CVI (TSH) : 29,3 %

• CVG (TSH) : 48,4 %

Sigma pour la TSH :

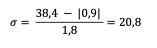
Interprétation du sigma pour la TSH :

• Performance exceptionnelle → 20,8 sigmas

• Bien au-delà de 6 sigma → le processus est extrêmement fiable

Comparaison des trois dosages (glucose, calcium, TSH) :

• Glucose : ~4 sigma → bon

• Calcium : ~1 sigma → peu performant

• TSH : ~21 sigma → excellente performance

V. Introduction de la composante biologique dans l’établissement des règles du contrôle qualité

V. Introduction de la composante biologique dans l’établissement des règles du contrôle qualité

Pourquoi les règles de Westgard posent problème pour la TSH ?

• Elles sont purement statistiques

• Elles n’intègrent pas la variabilité biologique

• Pour un test hyper performant (ex. TSH à 20 sigma), rejeter une série sur base de petites dérives est inutile

Comment introduire la composante biologique dans le contrôle qualité ?

Adapter la valeur cible de sigma :

• Viser 4 sigma comme standard (→ 99,38% dans la cible)

• Si performance supérieure, tant mieux ; sinon ajuster l’erreur totale pour atteindre 4 sigma

Que devient la formule du sigma pour le contrôle interne ?

• On considère le biais = 0 (car non visible sur les contrôles internes)

• La formule se simplifie :

Comment fixer l’écart-type pour viser 4 sigmas ?

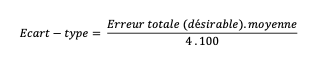
Exemple pratique : mise en œuvre multi-instruments pour le glucose ?

• On utilise 5 Alinity au CHU + 2 à ND de Bruyères

• Nouveaux lots de contrôle dosés 20 fois par machine

• On calcule la moyenne globale

• On ajuste l’écart-type pour garantir 4 sigmas (99,38 % de résultats dans la cible)

Application sur la carte de Levey-Jennings :

• On trace la moyenne ± 3 écarts-types

• Si un contrôle sort de ces bornes :

  • Risque que l’erreur ait un impact biologique

  • Rejet de la série

Avantage de cette approche « sigma + variabilité biologique » :

• Combine la statistique et la biologie clinique

• Rend le contrôle plus pertinent pour la pratique réelle

Exemples pratiques

Exemples pratiques

Quel contrôle est utilisé pour le glucose ?

• Un contrôle Brian (plasma ou sérum humain acheté)

• Achat de 10 contrôles, mélangés, aliquotés et conservés à –80 °C

Comment est établi le contrôle qualité pour le glucose ?

• Dosé 20 fois sur :

  • 5 automates Alinity du CHU

  • 2 automates Alinity de ND de Bruyères

Sur base de ces données :

• Moyenne = 103,75 mg/dl

• Ecart-type : 2,21 mg/dl (pas utilisé directement pour fixer le sigma ici)

• Erreur totale : 6,39%, basée sur la variabilité biologique (source : biologicalvariation.eu)

Quel écart-type appliquer pour viser un sigma de 4 ?

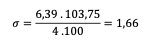
À quoi correspondent 3 écarts-types dans ce cas ?

3×1,66=4,98

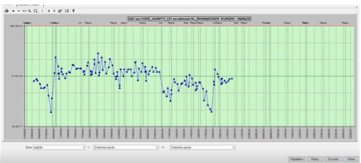
Que montre le graphique de Levey-Jennings avec ce contrôle ?

• Règle 10X et règle 4,1 S non respectées ponctuellement

• Mais le contrôle est commun à 7 machines, chacune ayant un petit biais individuel

Pourquoi ne pas appliquer strictement les règles de Westgard dans ce contexte ?

• Car la performance cible est fixée à 4 sigma

• Sur plusieurs machines, certaines valeurs seront un peu au-dessus, d’autres un peu en dessous

• Globalement, on reste dans la plage de performance acceptable

Quelle est la force de ce contrôle multi-machines ?

• Permet de travailler directement en fonction de l’erreur totale désirable

• Assure une homogénéité inter-instruments

• Rend les règles de Westgard moins nécessaires car le niveau sigma garantit la qualité