Geo proof and axioms with some def i forgot

Midpoint axiom

A line segment has one and only one

midpoint

The Midpoint def

Def. of midpoint: if a point is the midpoint of a line segment, it divides the segment into two

congruent parts

Bisector axiom

An angle has one and only one bisector

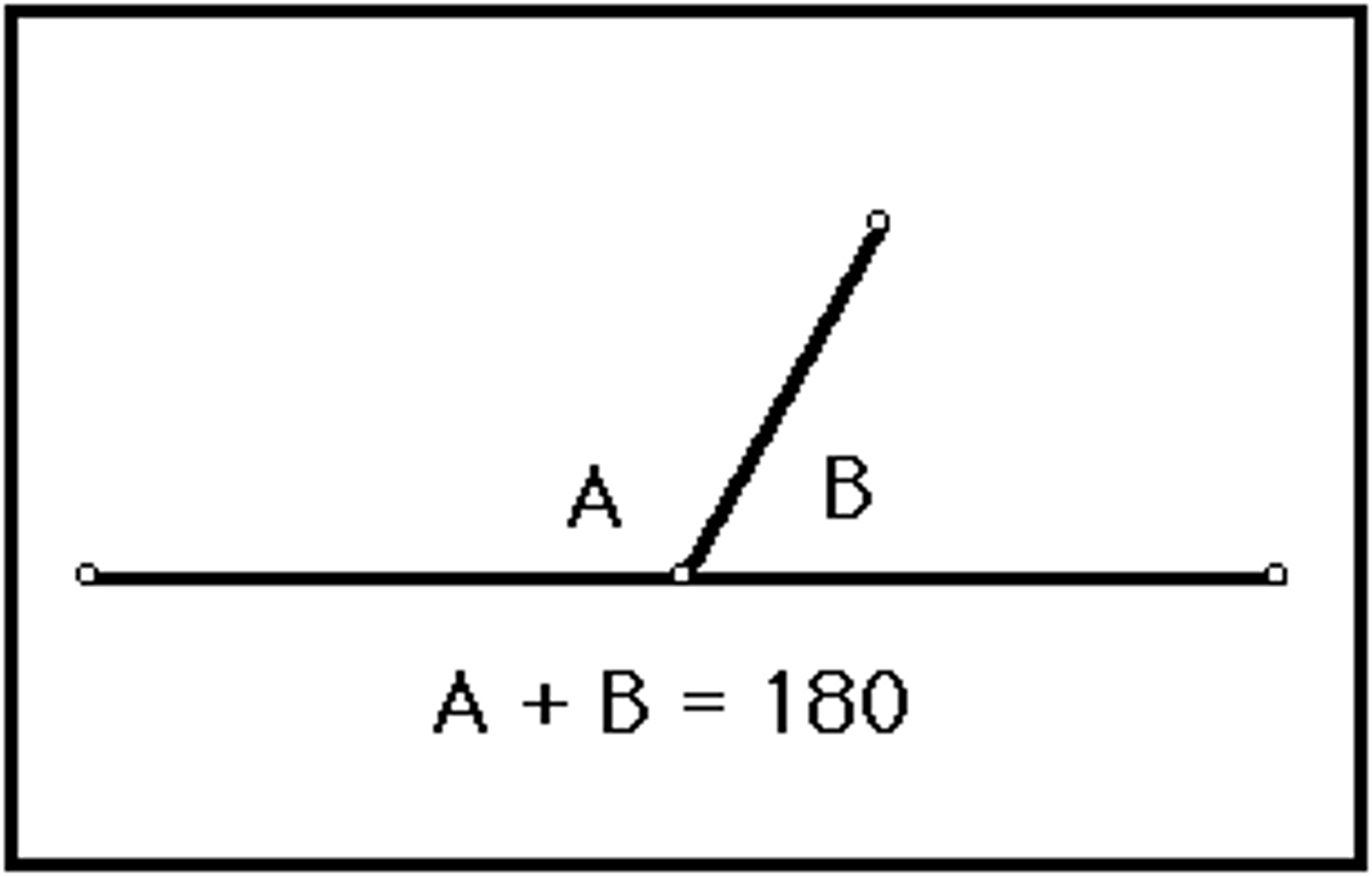
Supplement Axiom

The angles of a linear pair (?) are supplementary

Complementary axiom

The angles of a perpendicular pair are complementary.

Linear pairs

two adjacent angles whose non-common sides form a straight line

Perpendicular pairs

two adjacent angles whose non-common sides are perpendicular

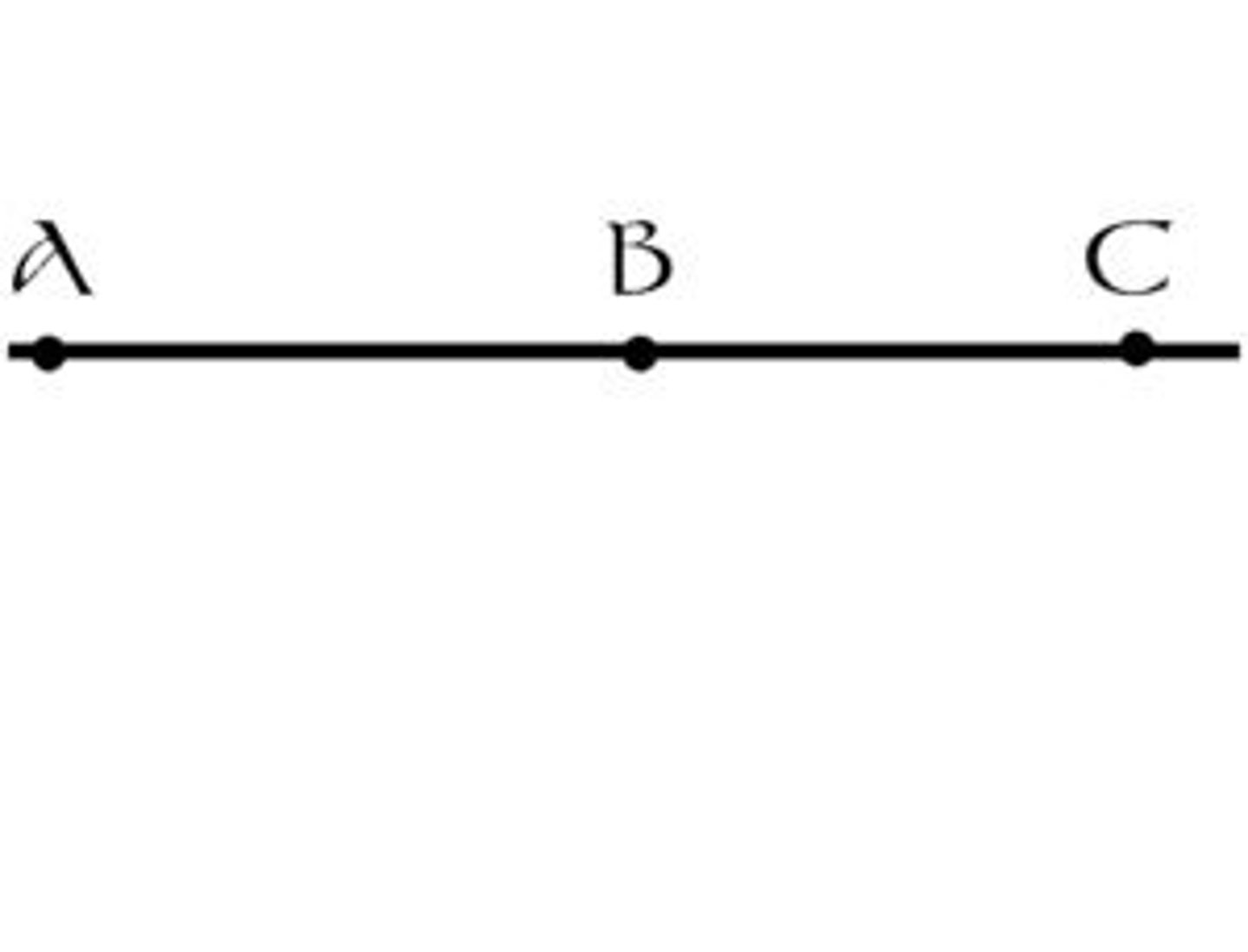
Collinear points:

Collinear points: ‐ points on the same line.

how many points make up a plane?

Axiom: For any three non‐collinear points, there exists one and only one plane

containing all three points.

i.e. Three non‐collinear points determine a plane.

Definition: Perpendicular Lines

Lines (or parts of lines) that intersect to form right angles.

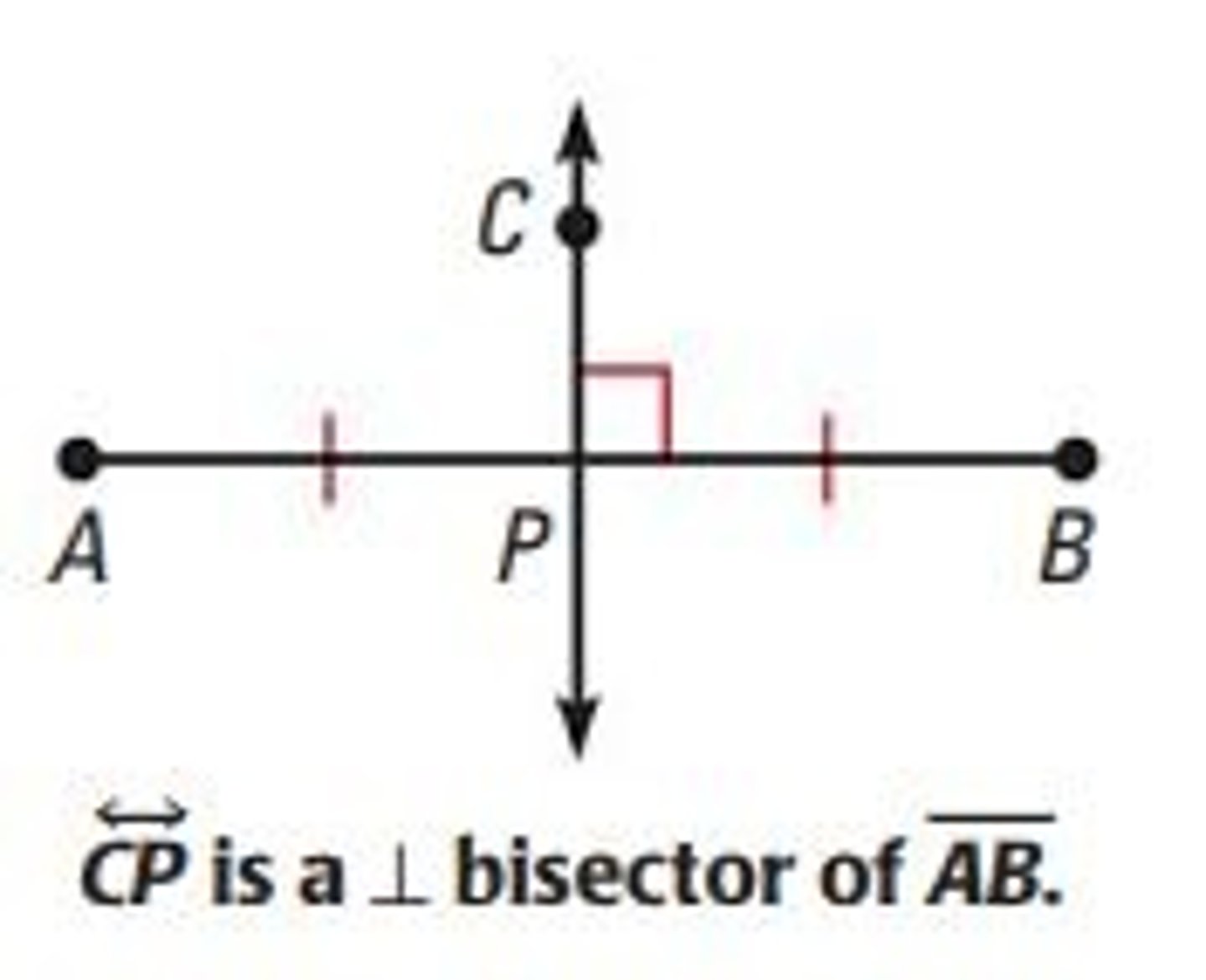
Definition: Perpendicular Bisector of a Line Segment

Lines (or parts of lines) that are perpendicular to

a line segment at its midpoint. (?)

Defintion of congruent angles.

Angles that have the same measure

segment additon axiom

The whole is equal to the sum of its parts.

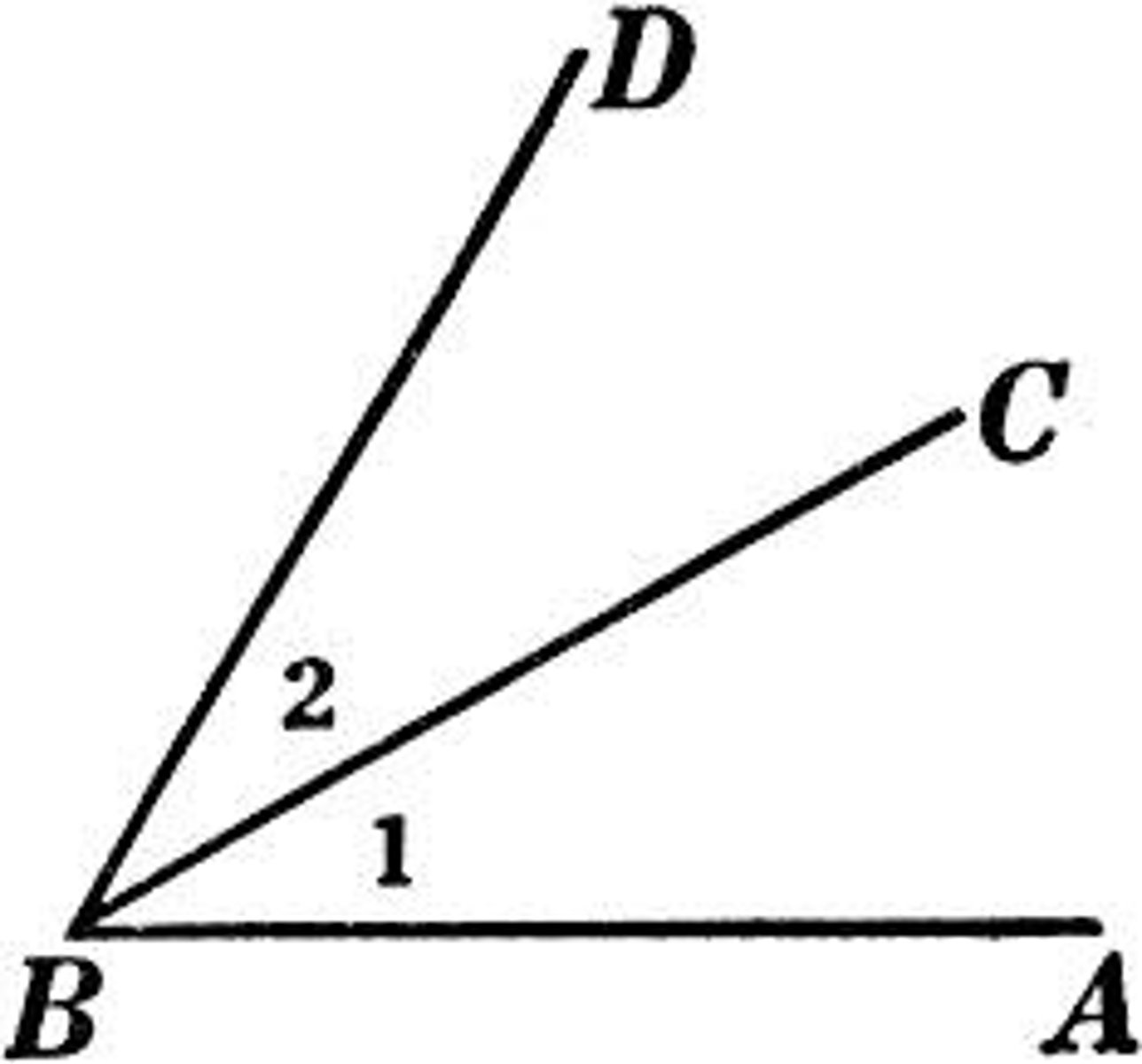
Definition of an angle bisector.

a ray that divides an angle into two congruent parts.

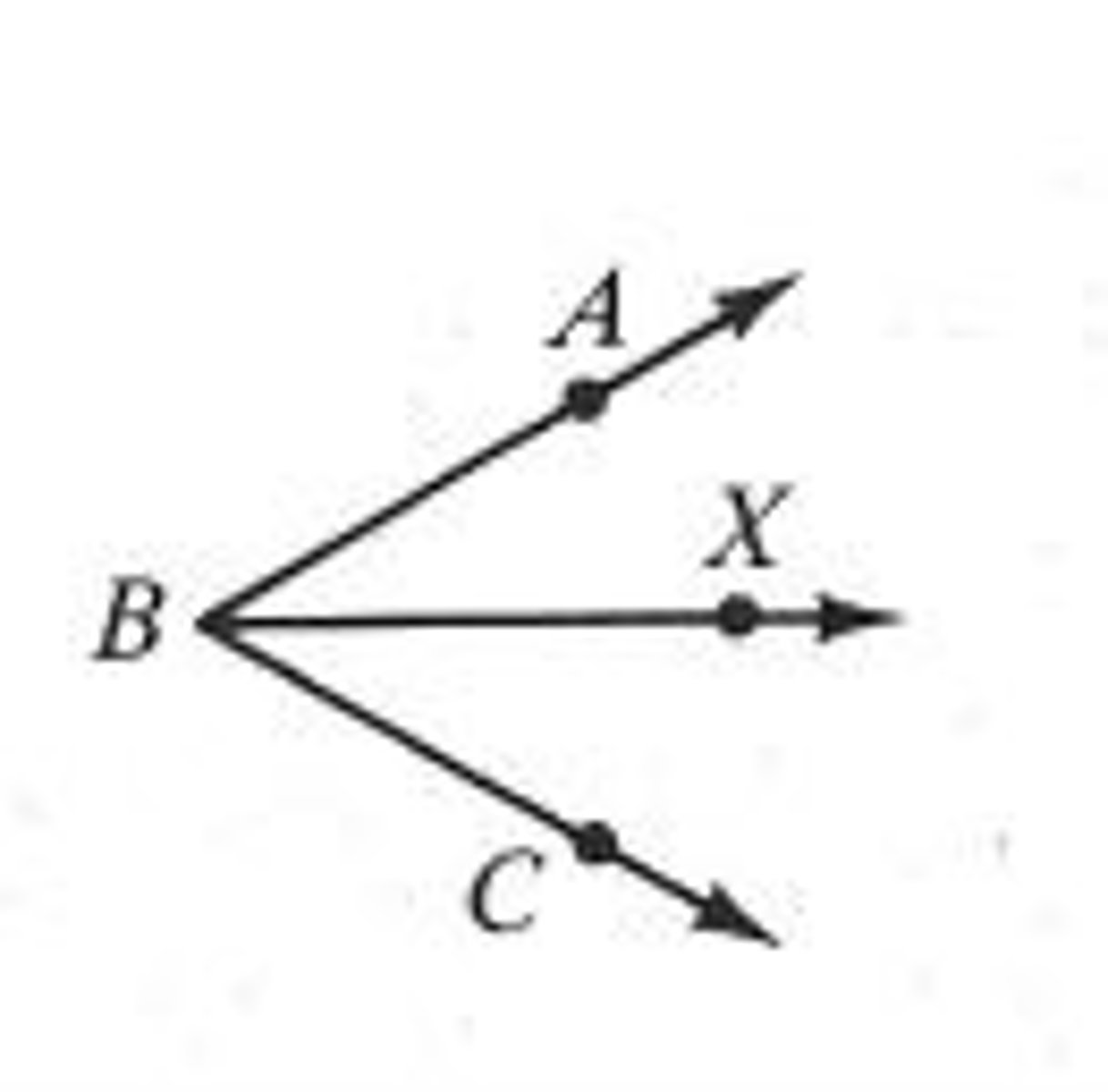
Definition of adjacent angles

Angle pairs which have

- A common vertex

- A common side

- no interior points in common.

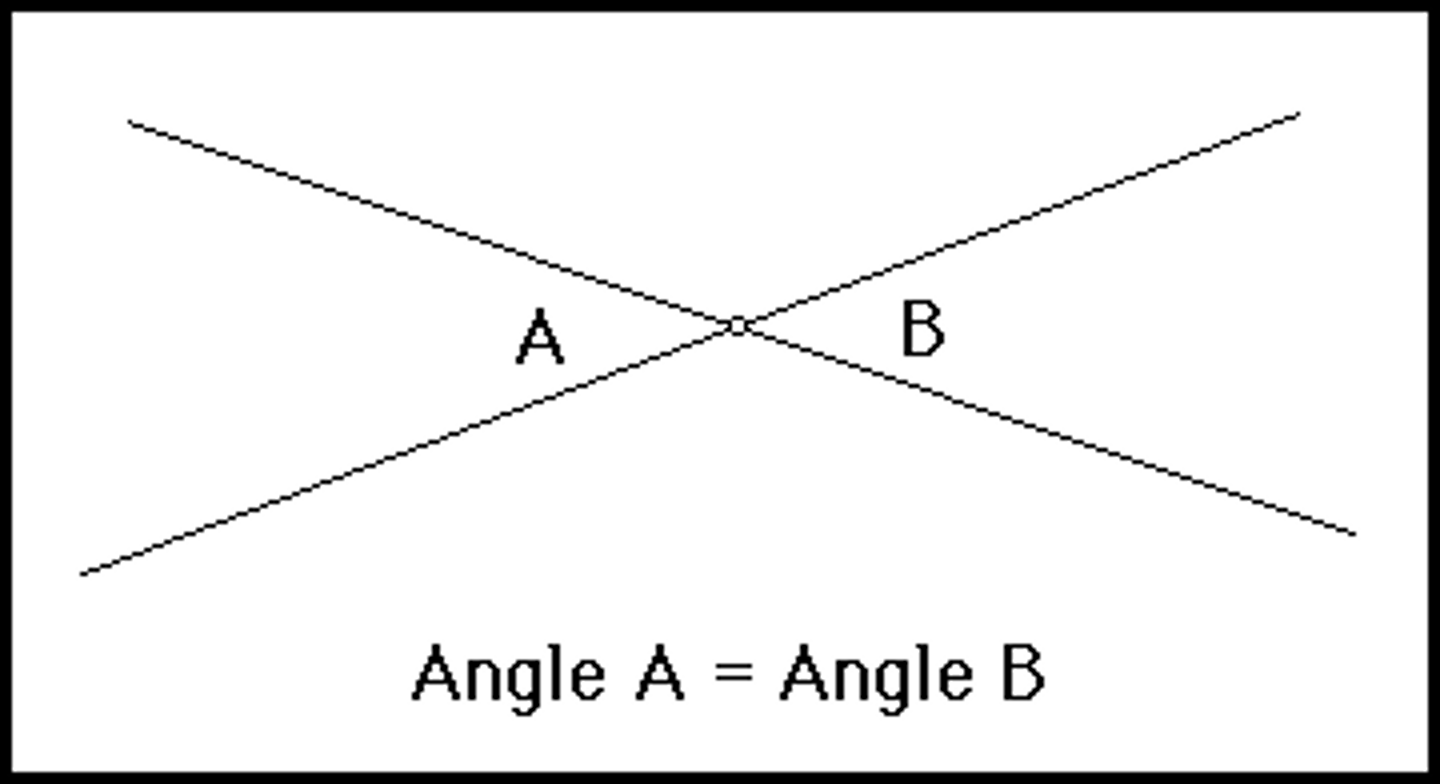
Definition of vertical angles.

two nonadjacent angles formed by two intersecting lines

Addition property

If equals are added to equals the results are equal

Subtraction property

If equals are subtracted from equals the results are equal

Multiplication property

If equals are multiplied by equals the results are equal

Division property

If equals are divided by equals the results are equal.

reflexive property

every quantity is equal to itself

symmetric property

Any quantity is equal in any order

If a=b then b = a

Transitive property

If a=b and b=c, then a=c

Substitution property

If two quantities are equal, they may be substituted for each other in any equation.

Supplement therom.

Suppliments to the same angle (congruent angles) then they are congruent?

Complement Theorem

Complements of the same angle (congreunt angles) are congruent.

Right Angle Congruence Theorem

All right angles are congruent.

Congruent Supplementary Angles Theorem

If two angles are congruent and supplementary then they are right angles.

Perpendicular Lines Theorem

If two lines intersect to form congruent adjacent angles then the lines are perpendicular

If two lines are perpendicular, they intersect to form congruent adjecent angles.

verticle angles are conguent.

Def of parallel lines

2 lines in the same plane that never intersect

skew lines

2 lines not in the same plane that never intersect.

Traversal

If two lines are cut by a third line

Corresponding angles

One exterior and one internal angle that are on the same side of a traversal and do not have a common vertex

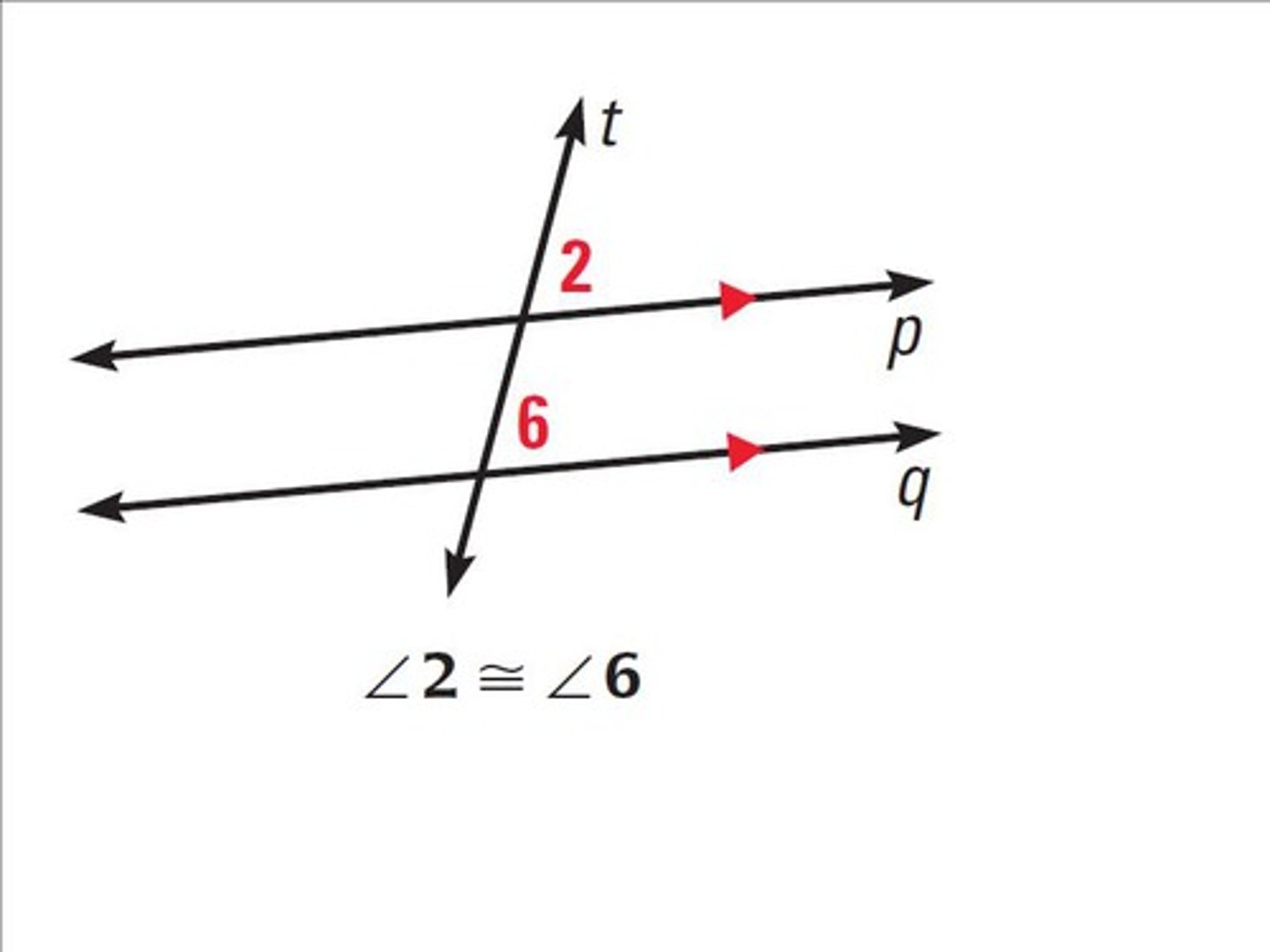
alternate interior angles

two angles on opposite sides of the traversal and do not have a common vertex.

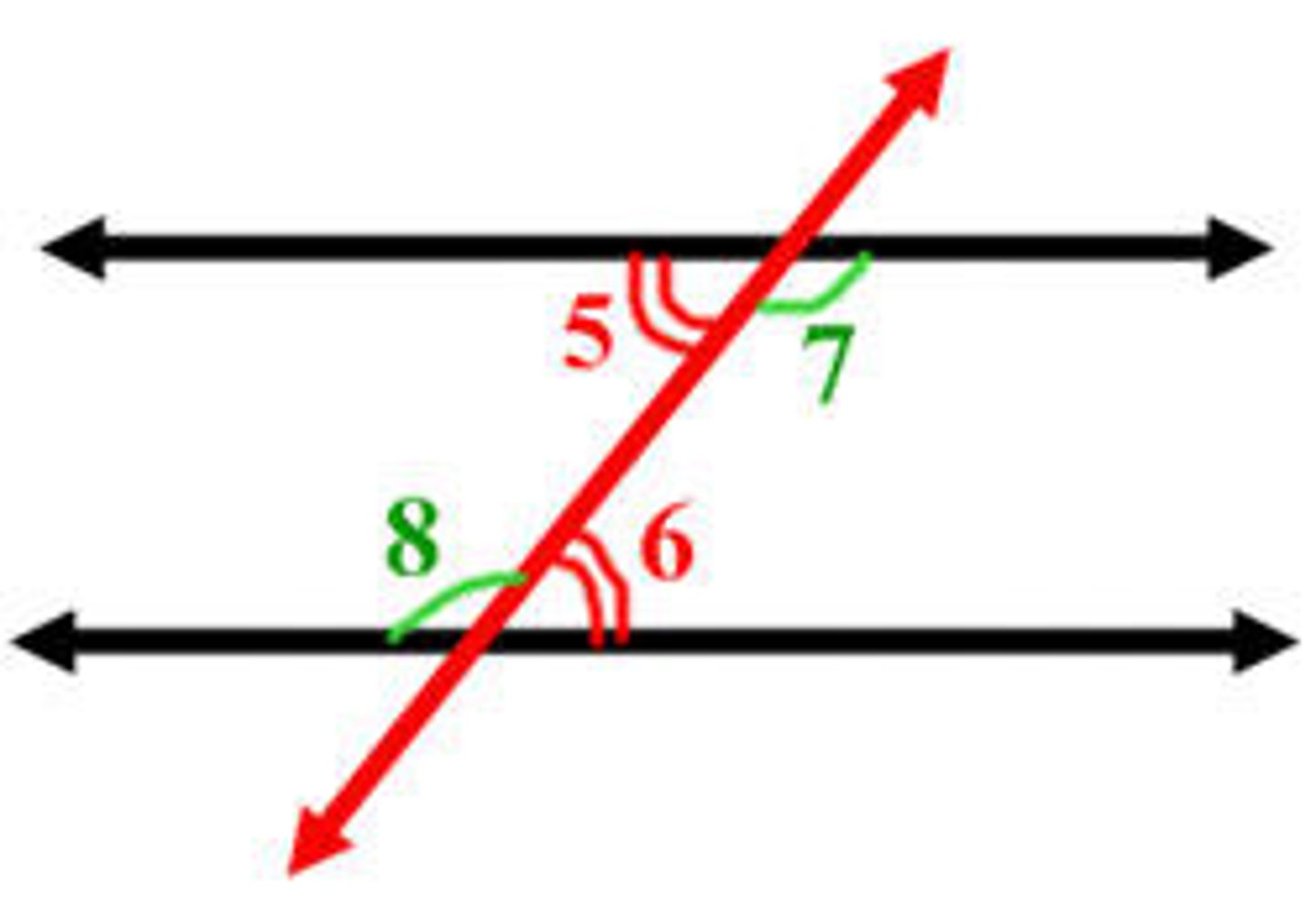
same side interior angles

Two angles on the same side of the traversal that do not have a common vertex.

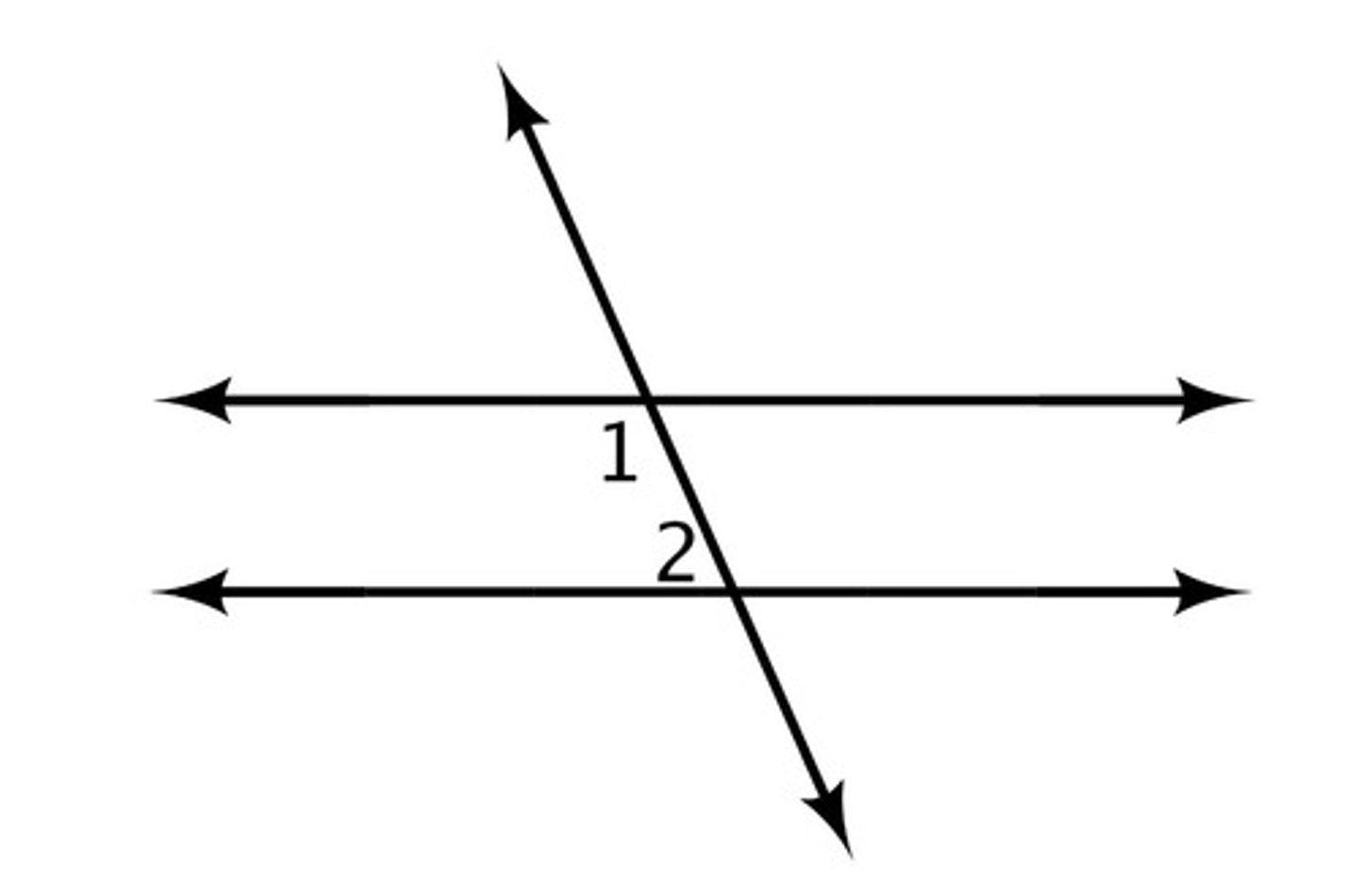
Euclid axiom

Through a point not given on a line there is exactly one parallel line to that given line.

Through a point not on a given line, there is exactly one perpendicular line to the given line.

Graws

small-big

Given

reflexive property

addition property

segment addition axiom (2x)

subsition property

Gwsrs

Big - small

Given

segment addition axiom (2x)

subsition.

Reflexive property

subtraction property

acute triangles

all three angles are acute

obtuse triangle

a triangle with one obtuse angle

right triangle

a triangle with one right angle

scaline triangle

A triangle with no even sides.

isosceles triangle

a triangle with at least two congruent sides

equilateral triangle

A triangle with three congruent sides

exterior remote therum

The exterior angles of a triangle equals the sum of the remote interoir angles.

Traingle 3 angles congurent theorum

If two angles of a triangle are congruent to two angles of another triangle, then the third angle is also congruent.

equalitral triangle theroum

each angle in an equilateral triangle is 60 degrees

acute angles comp therom

The acute angles in a right triangles are complementary.

Polygon

A figure that has at least 3 sides and straight lines

diagonal of a polygon

a segment connecting two nonconsecutive vertices of a polygon

Number of triangles in a polygon (?)

n-2

Sum of Internal Angles of a Polygon

180(n-2)

Measure of one angle in a polygon

180(n-2)/n

def congruent triangles

Triangles who's corresponding angles and sides are congruent.

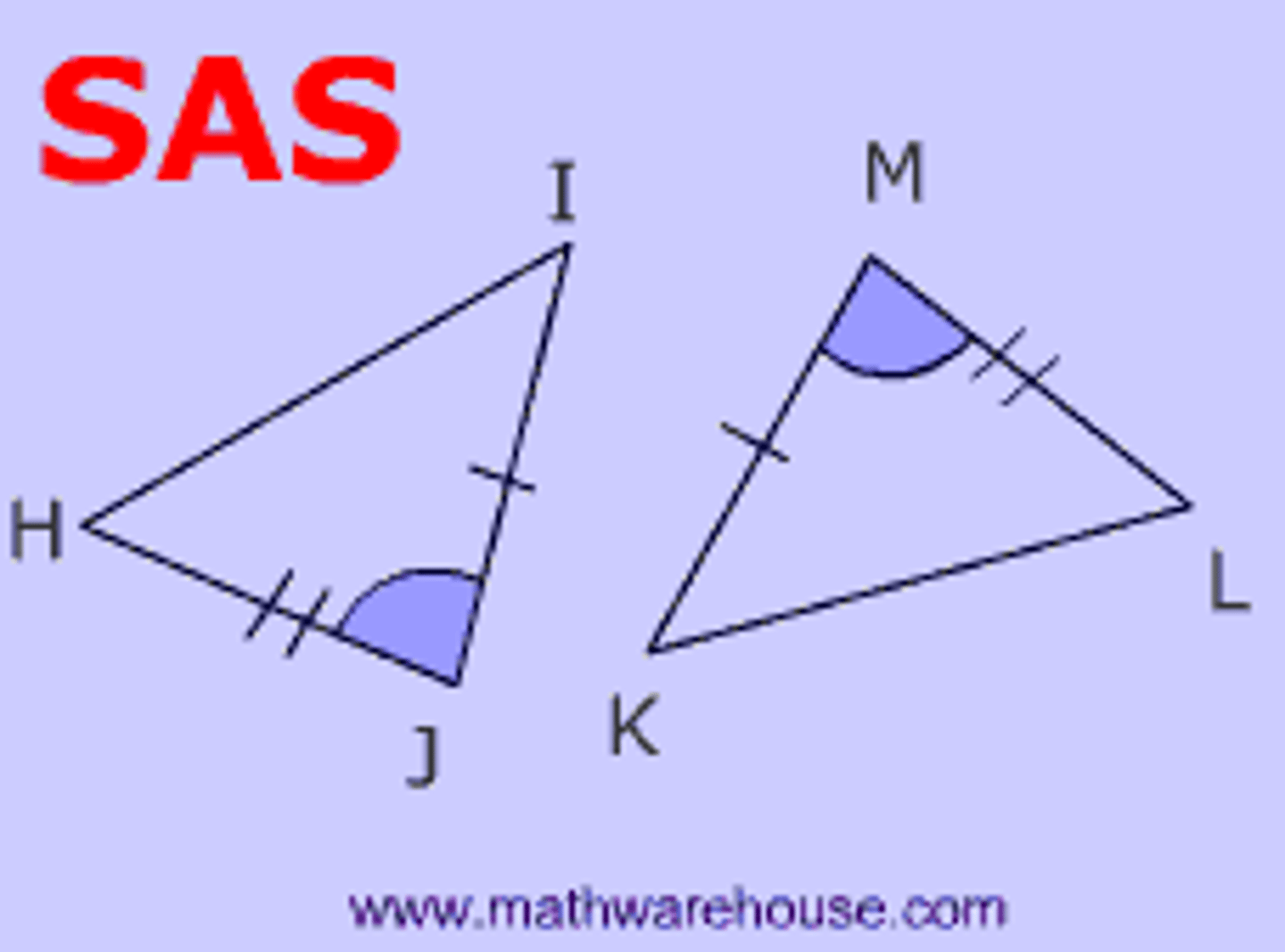
SAS congruence axiom

If 2 sides and the included angle of one triangle are congruent to the corresponding 2 sides and included angle of another triangle then the triangles are congruent

regular polygon vs non reuglar

A regular polygon is a geometric figure where all sides have the same length, and all interior angles are equal. For example, a square and an equilateral triangle are regular polygons.

In contrast, a non-regular polygon does not have this uniformity. Its sides can have different lengths, and its angles may not all be equal. For example, a rectangle (with equal opposite sides but differing lengths and widths) or a scalene triangle (with all sides of different lengths) are non-regular polygons.

Key Differences:

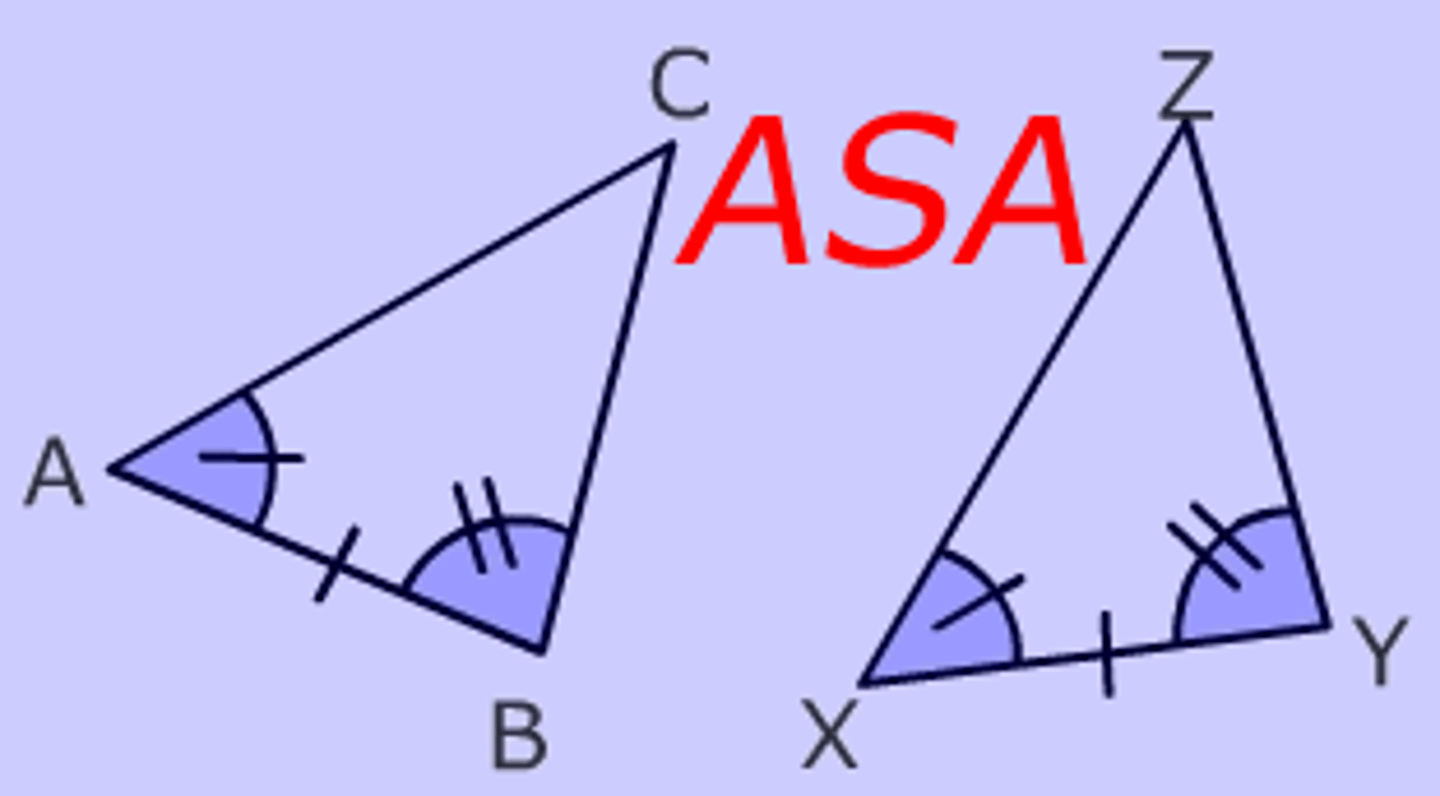
ASA Congruence Postulate

If two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the two triangles are congruent.

SSS Postulate

If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.

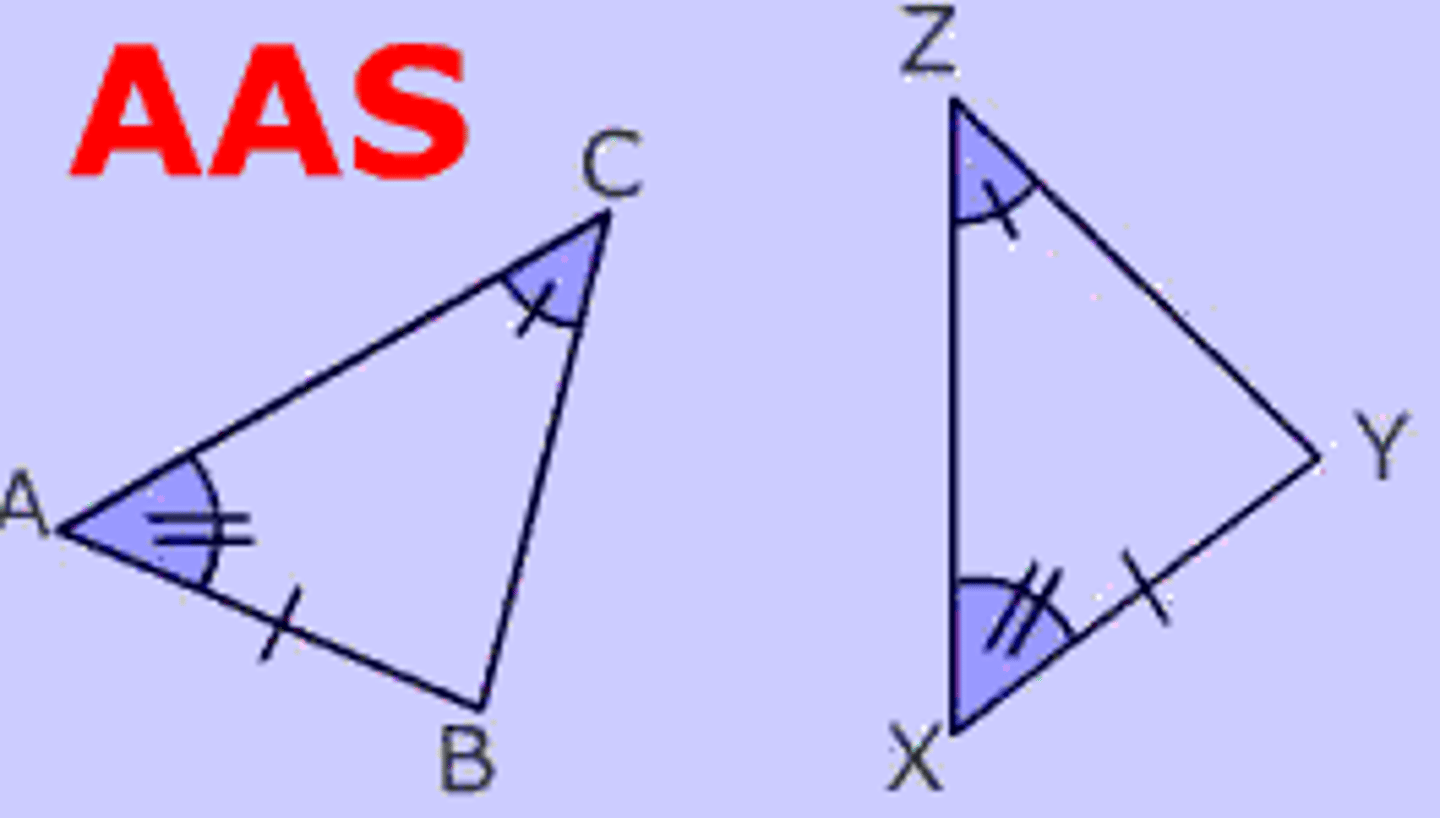
AAS Theorem

If two angles and a non-included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent.

CPCTC

corresponding parts of congruent triangles are congruent

Isocoilies congruence opposite angles therom

If two sides of a triangle are congruent, then the angles opposite them are congruent.

Isocoilies congruence opposite angles therom converse

If two angles of a triangle are congruent then the sides opposite the them are congruent.

Bisector of a vertex therom

The bisector of the vertex angle of an isosceles triangle is perpendicular to the base at its midpoint.

Equilateral triangle theroum

An equilateral triangle is also equiangular.

Angle bisecotr

An angle bisector is a segment in the interior of a triangle that bisects the angle

Where do angle bisecotrs intersect

All 3 angle bisectors of a triangle intersect at one point inside the triangle

Altitude

An altitude of a triangle is the perpendicular segment from a vertex to the line the contains the opposite side.

Acute triangle vertex

In an acute triangle, the 3 alternaives intersect at one point inside of a triangle.

In a right triangle how many altitues are inside a traingle

one inside, the other two are legs.

Where to the altitudes of a right triangle meet

In a right triangle, the three altitudes intersect at one point at the vertex of the right angle.

Where are the altitudes inside a obtuse triangle

In an obtuse triangle 1 altitude of the triangle and 2 are outside the triangle.

where to the altitues meet in an obtuse traingle

In an obtuse triangle 3, altitudes of a triangle intersect outside of the trinagle

median

A median of a triangle is a segment from a vertex to the midpoint of the opposite side

where to median interesct

3 median of a triangle intersect at one point inside of the triangle

HL congruence therom

In a right triangle, if the hypotenuse and a leg are congruent, then the triangles are congruent

3 steps of HL

Find two right traingles

state that there are two right triangles

prove the 2 hypothesis and legs to be congruent.

Trichotomy Property of Inequality

Either a>b, a

Addition property of inequality

If a

subtraction property of inequilty

If a > B then A-c > b-c

Multiplication prop of inequality

If x < y and Z > 0, then Zx < Zy

If x < y and Z = 0 then xz = yz

f x < y and Z < 0 then xz > yz

division property of inequality

X/ Z > Y/Z. if Z > 0

if Z = 0 then undifined

x/z < y/z if Z < 0

transitive prop of inequality

If a>b and b>c, then a>c

The whole is greater than any of its parts

if a = b + c and c > 0 then a > b

Theorem ( longer side larger angle)

In a triangle, the longer sides are opposite the larger angles, the shorter sides are opposite the smaller angles.

Converse (Larger Angle Longer Side)

In a triangle, the larger angles are opposite the longer sides, and the smaller angles are opposite the short sides

Corallary about perpendicular lines from point to line

The perpendicular segment from a point to a line is the shortest segment from the point to a line

Corollary about perpendicular lines with a point to a plane

The perpendicular segment from a point to a plane is the shortest segment from the point to the plane

exteriar angle greater theorum

the exterior angle of a triangle is greater than either remote interior angle

making up a traingle inqequlity theorum

The sum of the lenghts of any 2 sides of a triangle is greater than the length of the 3rd side

making up a traingle inqequlity theorum difference

The difference of the lengths of any 2 sides of a triangle is less than the lengths of the 3rd side

Definition of a paralleogram

If a quad is a parallelogram then the opposite sides of parallel.

Diagonal parallelogram theroum

A diagonal of a parallelogram creates 2 triangles.

opposite side congruent parallelogram

opposite sides of a parallelogram are congruent

opposite angle congruent parallelogram

ooposite angles of a parallelogram are congurent

consecutive angle supp parallelogram

Consecutive angles of a parallelogram are supplimentary

diagonals bisect parallelogram

the diagonals of a parallelogram bisect each other

two lines perp parell theorm

if two lines are perpendicular to the same line, then they are parallel to each other