Multiple linear Regression

The Regression process

• Check if dependant variable is continuous

• Estimate the model

• Analyse residuals

• Check is the assumptions are verified

• examine the goodness of fit model

• Is the overall fit significant

• Is the model the best

5 assumptions of multiple linear regression

• Linearity

• homoskedacity

• Independance of errors

• Normality of residuals

• No collinearity

Scatterplot matrix

Helps to better understand the model

Scatter plot of residual against dependant variable

detect outliers

Scatter plot of residual against dependant variable

confirm outliers and look for broken assumptions

normal q-q plot

Compare the distribution of the residuals to a normal distribution

Partial regression coefficient

Coefficient that describes the effect of a one-unit change in the independent variable on the dependent variable, holding all other independent variables constant.

If a regression model is estimated using all five independent variables

any prediction of the dependent variable must also include all five variables

R²

Sum of square regression / Sum of square total

Evolution of R² When you add variables

R² can not decrease

Problems with R²

• R² Do not say wether coefficient are statistically significant

• R² do not say anything about biases

• R² do not say if the model is a good fit

Overfitting

model is too complex, meaning there may be too many independent variables relative to the number of observations in the sample

Adjusted R²

What does it mean if adjusted R² increase or decrease

new coefficient t stat is superior / inferior to 1

Who is bigger R² or adjusted R²

R²

AIC

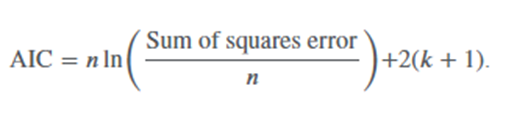
BIC

BIC impose a greater penalty on more complex model

When do you use AIC or BIC

• AIC is for prediction

• BIC is for testing fit

Nested model

Models in which one regression model has a subset of the independent variables of another regression model.

F stat for restricted model

Summary Model Fit

general linear F test

R² and adjusted R² are not generally suitable for testing the significance of the model’s fit; for this, we explore the ANOVA further, calculating the F-statistic and other goodness-of-fit metrics.

ok

Principles of model specification

• Grounded in economic reasoning

• Parsimonious

• Perform on other samples

• Model should adapt to non linearity

• Model should satisfy regression assumptions

Failures in regressions

• Omitted variables

• Innapropriate form of variables

• Inaproprate variable scaling

• Innapropriate data pooling

Heteroskedacity

Variance of residuals differs across observation

Interpretation of Breusch Pagan test

the null hypothesis is that there is not heteroskedacity. This is a one tail risght side test.

What model should you use if there is heteroskedacity

Robust standards errors

Serial Correlation

Often found in time series. Residual are correlated

Impact of Serial Correlation on Multiple regression model

First order serial correlation

The correlation is about the adjacent residuals

VIF interpretation

VIF > 5 so investigate
VIF > 10 serious multicolinearity

How you correct multicollinearity

• Exclude variables

• Using a different proxy

• Increasing the sample size

high leverage point

An observation of an independent variable that has an extreme value and is potentially influential.

An outlier

An observation that has an extreme value of the dependent variable and is potentially influential.

How to identify ouliers and high leverage points

Scatterplot

Leverage

A value between 0 & 1 to identify how far is the high leverage point (1 being the highest)

How to detect high leverage point

Higher than 3 x (K+1/N)

Method to identify outliers

Studentised residuals

degree of freedom for studentised residuals

n-k-2

Conclusion of studentised resiudals

if studentised residuals are higher than Critical value then it is an outlier

Number of dummy variable for N categories

N-1

Qualitative dependant Variables

logistic regression

The log of the probability of an occurrence of an event or characteristic divided by the probability of the event or characteristic not occurring.

Model used to estimate coefficient in logisitic regression

Maximum likelyhood ratio

error distribution for logistic regression

the distribution’s shape is similar to the normal distribution but with fatter tails.

how to assess logistic model fit

Likelyhood ratio test

LR = −2 × (Log-likelihood restricted model − Log-likelihood unrestricted model)

Interpratting log likelyhood test

log-likelihood metric is always negative, so higher values (closer to 0) indicate a better-fitting model.

General linear F test