Chapter 7 - Modelling growth and decay using recursion

Modelling growth and decay using recursion - Chapter 7 Key Terms

Sequence

A list of numbers written in succession (order) or progression.

Random Sequence

A sequence where numbers are not related by a rule.

Rule - Based Sequence

A sequence where numbers are related by a rule.

Terms

Numbers in a sequence.

Successive Terms

Next term in the sequence.

Previous Term

Terms that were before.

Term Numbers

*Most will be denoted as v in the exam

u₀ - Initial Term of Sequence (usually provided by the question, MUST INCLUDE)

u₁ - First Term of Sequence

u₂ - Second Term of Sequence

u_n - nth Term of Sequence

Previous Term of u_n: u_n-1

Successive Term of u_n: u_n+1

Recurrence Relation

A mathematical rule (equation) that can be used to generate a sequence. Generates one term at a time. Links successive terms.

Recurrence Relations Symbols

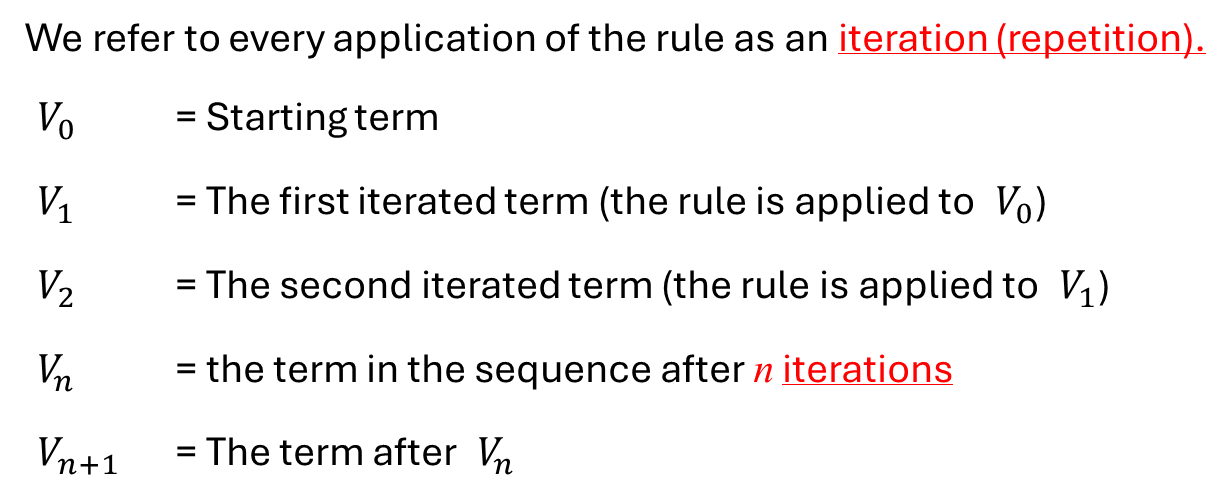
Linear Growth

When a quantity increases at regular intervals by the same amount each time. (E.g. Simple Interest)

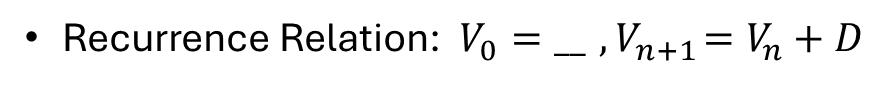
Linear Decay

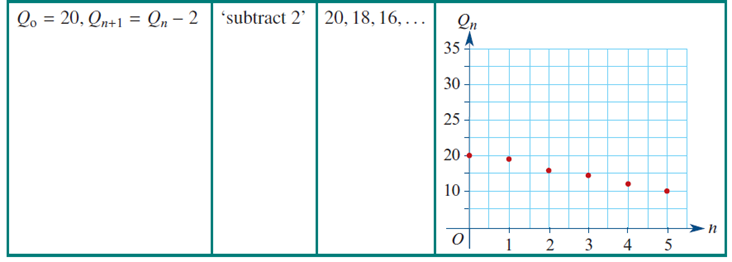
When a quantity decreases at regular intervals by the same amount each time. (E.g Unit cost depreciation and flat rate depreciation).

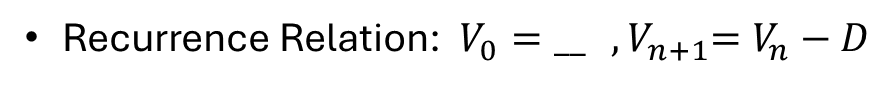
Simple Interest Formula

I = Prt/100

Where P = Amount invested or borrowed IN YEARS (i.e. loan), r = interest rate per annum, t = time in ALWAYS YEARS

Need to convert into years when using this formula!

Principal

The starting amount borrowed for a loan or the starting amount invested in an investment.

Interest

Monthly charge for borrowing money, typically expressed as an annual percentage rate.

Recurrence Relation for Simple Interest

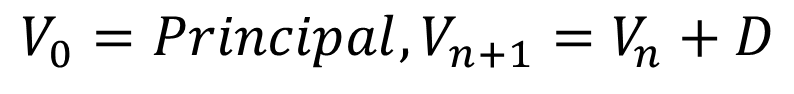
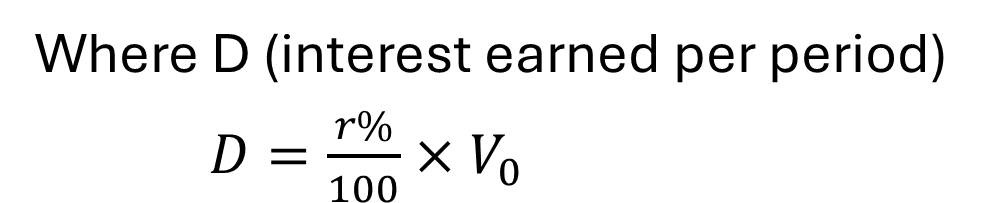
Amount of Investment

Depreciation

The decrease or loss of the value of an item over time.

Depreciation (D) = unit cost x n → n = value of units produced.

Future Value

The likely value of an item at some point in time.

Scrap Value

The value of an item when it is sold off or disposed of. When this happens, the item is written off, meaning it is no longer available.

Flat-Rate Depreciation

NOTE: D = r/100c * V0

Recurrence Relation: V0=…, Vn+1 = Vn-D

RULE: Vn = V0-nD

Unit-Cost Depreciation

When the future value of an item decreases based upon use rather than the age of the item.

Recurrece Relation:

NOTE: D = Depreciation per Output

Recurrence Relation: V0=…, Vn+1 = Vn-D

RULE: Vn = V0-nD

Length of Time in Use (t)

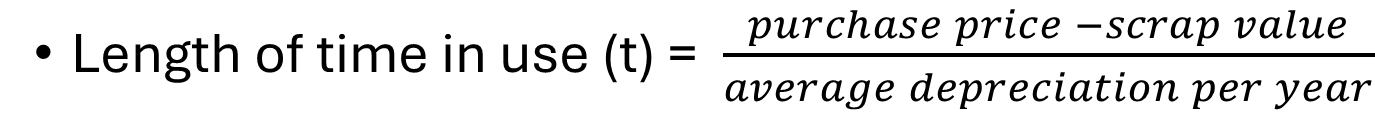
Annual Interest Rate (r)

r = A-P/P*t, A = Final Amount, P = Principal, t = time

Book Value (V)

Book value (V) = Purchase price – (unit cost x n)

Unit Cost

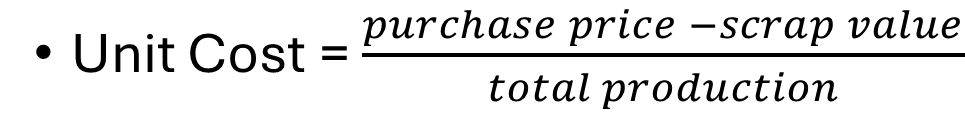
Geometric Sequence

An ordered set of numbers that progresses by multiplying or dividing each term by a common ratio. NON-LINEAR, EXPONENTIAL.

Recurrence Relation for Geometric Sequence

Recurrence Relations for Compound Interest

Compounding Period

13 FORTNIGHTS IN 6 MONTHS!

Reducing Balance Depreciation RR

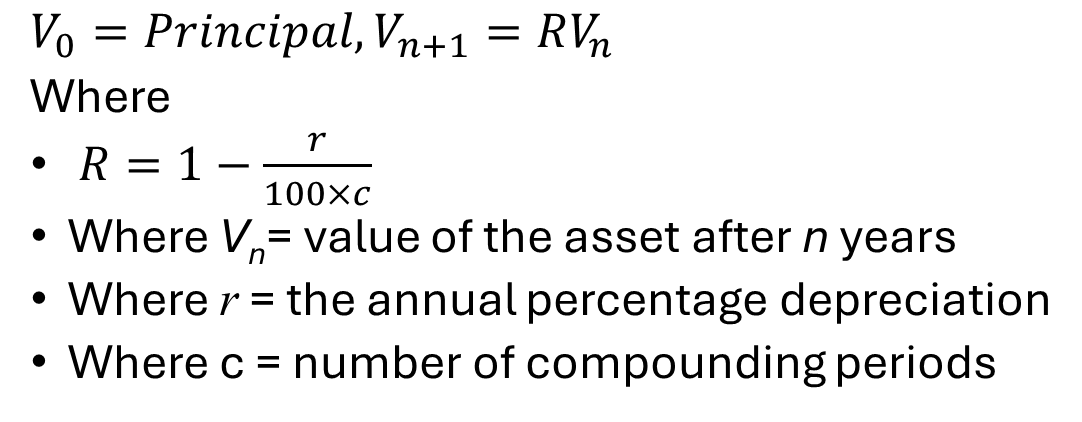
THE ONLY ONE THAT HAS R<1!

Explicit Rule for Geometric Growth / Decay

Vn = Rⁿ*V0 (multiplying R repeatedly)

Compound Interest Loans and Investments

Reducing-balance depreciation Rule

Interest for Geometric Growth or Decay

Interest = V0 - Vn for decay

Interest = V_n-V₀ for growth.

Negative since the book value of an item is decreasing

Nominal Interest Rate

Compound interest rates are usually quoted as annual rates, or interest rates per annum. This annual interest rate is nominal interest rate (名义上银行给你的).

Effective Interest Rate

The actual amount of interest earned as a percentage of the initial amount over one year.

MORE Compounding period, HIGHER Effective Rate (more money earnt)

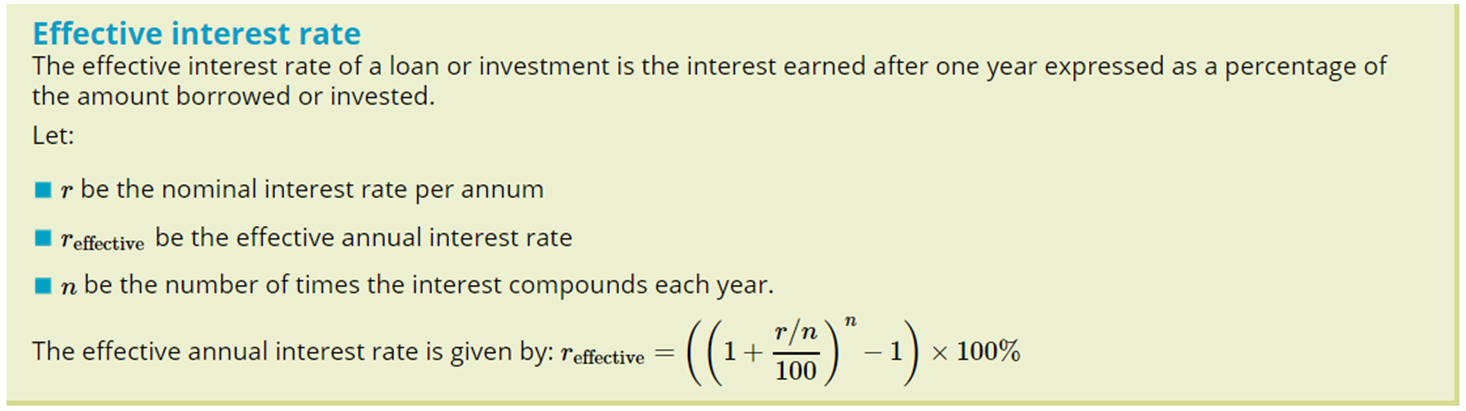
Exam Tips

• ‘After’: interest = Vn-V0

• ‘In’: interest = Vn-Vn-1

• R > 1: (R - 1) * 100 * C

• R < 1: (1 - R) * 100 * C

• Perpetuity Amortization: Interest earned = (r / 100 C) V₀

• Rounding: 300.09 rounds to 301, 300.0001 rounds to 300, 299.87 rounds to 300

• Decimal Places: Use 2 decimal places unless specified.

• INCLUDE BRACKETS!

  ---

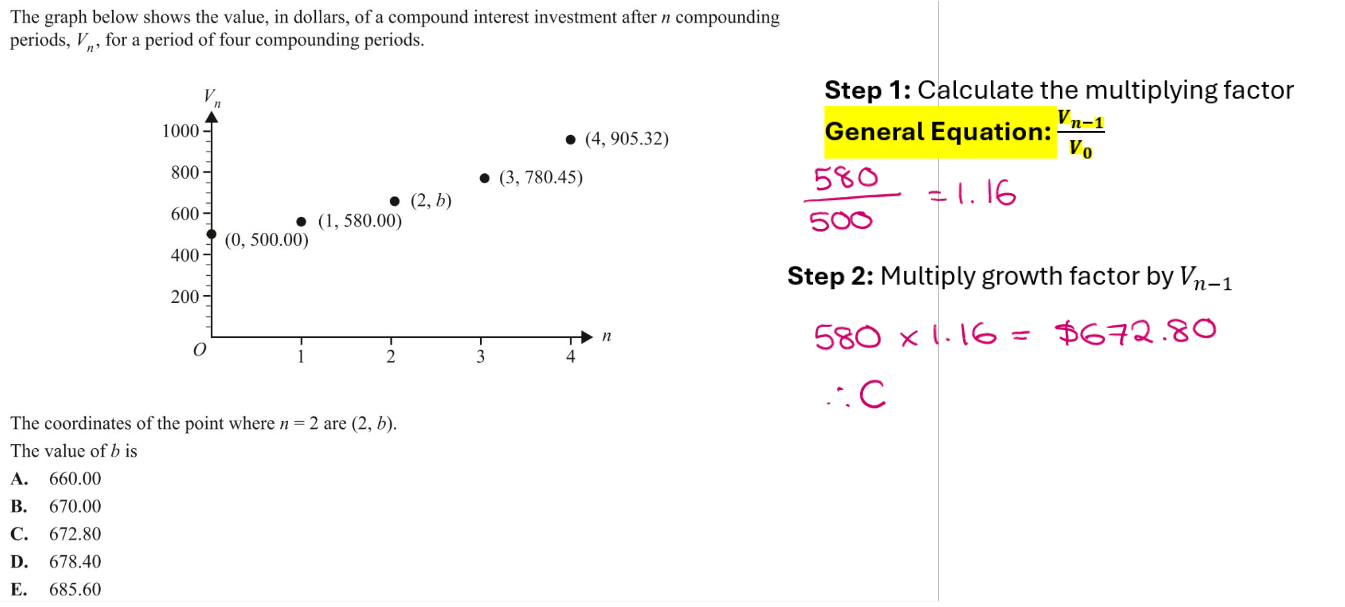
• Refer to picture on right:

• Use V_n-1/V₀ to find growth factor;

• Multiply growth factor by V_n-1