Light: Quantum Model

Blackbody Radiation and Blackbodies

the radiation emitted by a black body at a constant temperature

Blackbody - idealised object that absorbs all electromagnetic radiation it encounters

• Perfect absorber of EM radiation ∴ any EM radiation it emits must be made by itself

  • Any radiation emitted comes from the particles on the surface of the BB

  • Any radiation from inside the object is absorbed and re-emitted

• The closest thing we have in the universe are stars

Thermal radiation – electromagnetic radiation emitted by an object due to its temperature

Colour it glows depends on

• TEMPERATURE: Temp increases = wavelength shortens (more kinetic energy), brightness increases (E∝A^2)

  • Low temperature  thermal radiation is mostly in infrared (not observable = black)

  • As temperature increases, object glows more red → yellow → white → blue (less short wavelengths)

• The properties of the object: its elemental composition

Nature of Blackbody radiation

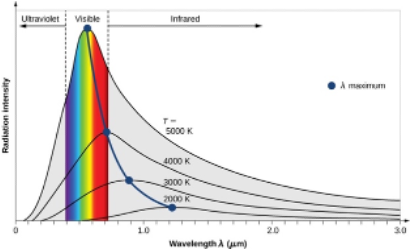
Typical blackbody spectrum: (power/intensity/energy vs wavelength)

• Area under the line = total energy produced by star

• Intensity is zero at short wavelengths

• As temperature increases:

  • The graph shape shifts to the left → more shorter wavelengths

  • λ_max increases (higher peak)

    • since P_total ∝〖Temp〗^4

  • Higher intensity/power for all wavelengths

Follows Wein’s Law: λ_max∝1/T

Classical Explanation of BB radiation vs Experimental results

Classical theory of thermal radiation

Developed during the 19th century using Wein’s law and Maxwell’s theory of light

• An object at some temperature would emit EM radiation

• Having temperature = has kinetic energy = particles are oscillating in the object

• Particles would collide exchanging energy

• Particles are accelerating = produces EM waves → according to Maxwell’s model of light

• Thermal radiation originates from accelerating charged particles

Classical prediction of the blackbody spectrum

1. All frequencies of oscillation are equally likely

   1. More power is emitted at higher frequencies since there are more high frequencies (shorter wavelength)

2. Each particle emits radiation at the frequency at which it oscillates

3. Each particle will emit the same amount of energy on average (amplitude)

   1. High energy particles will cancel out the low energy ones

   2. Equal power is emitted at all frequencies

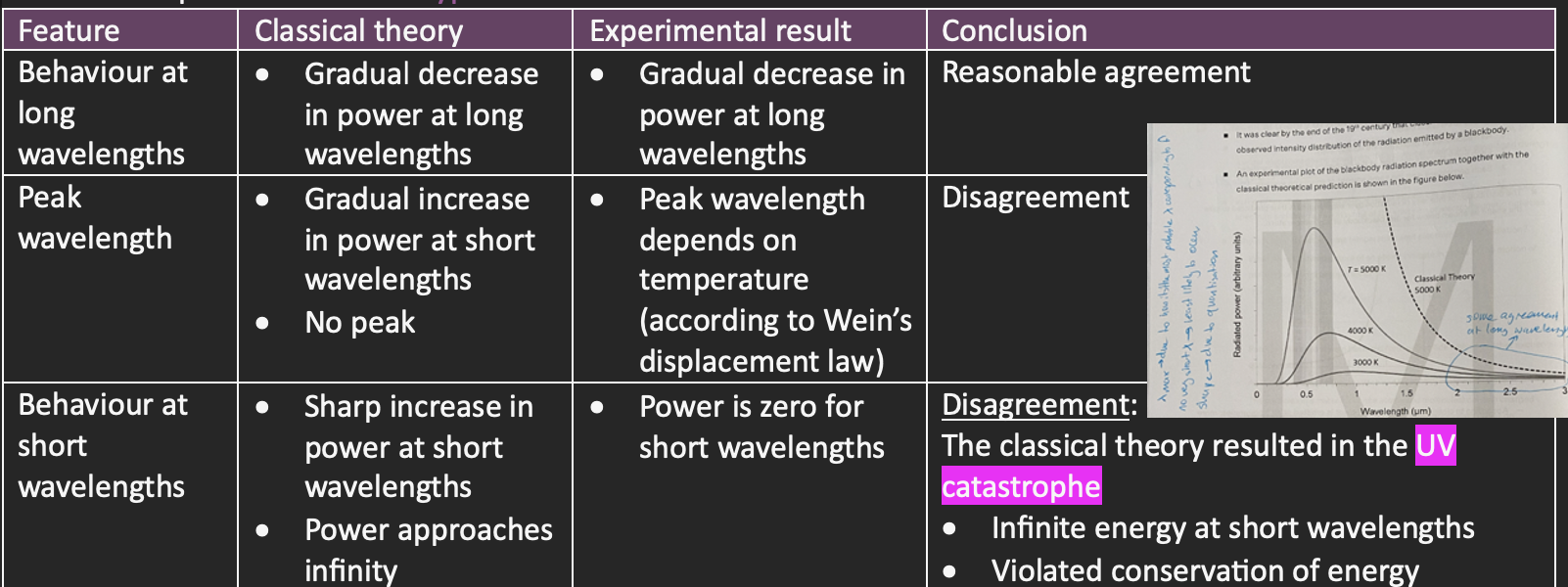
This resulted in the UV catastrophe, as at short wavelengths, an infinite amount of energy was being emitted

→ Could not explain experimental results, so a new theory regarding the nature of light was required

Classical theory vs experimental result table comparison

Planck’s Model of EM Radiation Emitted by Black Bodies (Quantum Era)

Assumptions made by planck

1. All frequencies were not equally likely → maximum wavelength was the most common frequency

2. Each particle will not emit the same amount of energy on average → each particle has different energy levels due to its elemental composition, and when moving to different levels, it will need to release or absorb a specific amount of energy (E=hf)

3. Intensity of radiation would increase by fixed amounts depending on the frequency: f = ΔE/h

4. These fixed amounts are thought of quanta (discrete packets of energy)

Hypothesised that

• All accelerating charges can only oscillate at specific frequencies, and thus have discrete energies

• EM radiation was released in quanta (before called photons) with energy E=hf, not waves

• At each temperature, there is some frequency of oscillation that is most likely for the charges

  • Since on average, more charges are oscillating at this frequency, it will be more emitted instantly

• Higher frequencies require individual charges to have lots of energy → unlikely for these charges to poses enough energy to emit them = no emission of very short wavelengths

• Temp of BB increases = Kinetic energy of charges increases = They move faster, collide more frequency =Emit more quanta of EM radiation per second = brightness/power increases = More quanta are at higher frequencies = shift towards shorter wavelengths

Plank’s Contributions

atoms occupy discrete energy levels → energy is released in quanta → frequencies are discrete → total energy released is integer multiples of e=hf

Maxwell’s vs Planck’s view of EM radiation

Plank’s energy equation for photons

Energy can be measured in eV

Electron volt (eV) – the energy (ΔE) gained by a particle moving through a potential difference, which is equal to the charge (e) times the potential difference (V

• Uses equation W=qV

• A unit of energy: 1eV = 1.602x10-19J

• J → (÷ 1.602x10-19) → eV (going to a bigger number)

• eV → (x 1.602x10-19) → J (going to a smaller number)

Wein’s Law

relates temperature of a blackbody with its peak wavelength

λmax=b/T

Where

• λ_max = the peak wavelength (m)

• b = Wein’s displacement constant (b = 2.898x10-3)

• T = temperature (K or Kelvin) → MUST BE IN KELVIN (SI UNITS) DUE TO CONSTANT

  • Kelvin = Celsius + 273

  • 0K = -273°C

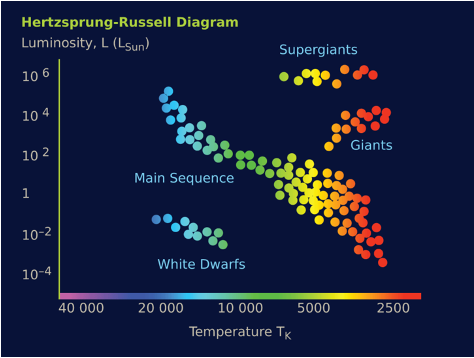
Hertzsprung-Russell diagram

Impact of peak wavelength

• Red stars are cooler than blue stars

Impact of size (radius)

• Larger stars are brighter than smaller stars (red supergiants are more luminous than red stars on the main sequence)

For main sequence stars  where most stars are located on the graph

• Hotter temperature (bluer) = more luminous

Impact of mass (no. of charges inside)

• Larger mass = more gravitational force = higher pressure in core = more nuclear fusion = hotter = shorter life span = more luminous (for main sequence)

• Smaller mass = less fusion = cooler = less luminous (for main sequence)

Over a star’s life cycle, it can change where it lies on the graph

→ Note: its mass doesn’t change on a broader level (atomically, it does since E=mc² but its density and chemical composition does

Einstein’s Photon Theory of Light

Einstein extended Planck’s concept of quantisation of electromagnetic radiation in order to explain the photoelectric effect

• Frequency is related to the amount of each energy a photon carries

• Intensity is related to the number of photons per second

He postulated:

1. Light (any EM radiation) is a stream of massless, fundamental particles called photons

2. Each photon contains the energy E=hf, as determined by Planck

3. Energy of the beam of light is localised to each photon, not spread across the wavefront of the light beam

4. There is always a one-to-one interaction between photons and electron → one photon is absorbed/released by one electron at a time

Properties of light explained by wave and particle behaviour

The Photoelectric Effect and competing theories

phenomenon where electrons are ejected from a metal when light is shone on the metal surface

• Photoelectrons – electrons emitted by photoelectric effect

• Whether it occurs depends on the frequency of light

Theory	Maxwell (transverse)	Einstein (photon)
Location of energy	Across wavefronts	In photons
Absorption of energy	Continuous	Discrete
Explanation of photoelectric effect	Classical theory → all frequencies of EM can cause effect, emission only depends on time and intensity Any EM radiation incident on a surface of a metal will cause the electrons to oscillate The greater intensity of any frequency would cause the electrons to oscillate more Eventually with so much energy they would break free from the metal	Quantum theory Light consists of photons with energy of E=hf These photons have one to one interaction with electrons in the metal The electron absorbs this energy and uses it to escape the electrostatic force binding it in the metal The weakest bound electrons (the ones at higher energy levels) only need energy equal to the work function (ɸ) to escape Threshold /minimum frequency (f= ɸ/h) required to overcome the work function in the first place Any leftover energy after overcoming the work function becomes kinetic as the electron exits the metal (Kmax = hf-ɸ) Greater intensity = more photons, hence more emission of photoelectrons (since interactions)
Factors that impact the properties of photoelectric transmission	No. of photoelectrons and their Kmax are dependant on intensity of light	No. of photoelectrons per second → Depends on: Intensity of light + must be above threshold frequency for emission in the first place Largest (initial) kinetic energy of photoelectrons →Depends on: Frequency of light (higher frequency above threshold frequency = more energy in photon = more energy leftover after overcoming work function= Kmax increases)
Was it correct?	No	Yes

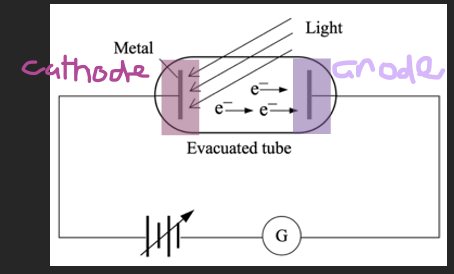
Experimental set up for photoelectric effect

1. A high potential difference between the cathode end (- side) and the anode (+ side)

2. This potential difference creates electric field lines

3. When a light of a specific frequency or higher is shone onto the cathode, electrons can break free and jump off the metal

4. They then accelerate to the anode

5. Pass through the anode and an ammeter measures the current (rate of photoelectrons passing through)

Results of photoelectric experiment → impact of different factors on photoelectric current

Impact of frequency on current (no. of photons emitted)	Electric current remains constant as light frequency increases (flat line)
Impact of Intensity on current (no. of photons emitted)	Current increases with the intensity of light (LINEAR), not frequency Intensity increases = more photons being emitted = more photons to interact with electrons = photoelectric emission increases = current increases No EM radiation on the metal = no emission When a low intensity monochromatic (single wavelength) of high enough frequency, there is photoelectric emission (current flows through the ammeter)
Impact of changing the voltage difference between plates on current	As anode voltage becomes negative it is called the stopping electrode Less e- can reach plate A due to the repulsive force from the anode Eventually the repulsive force is so strong that no e- can travel across The current is zero  this is the stopping voltage As voltage increases, the photoelectrons can accelerate from the cathode to the anode faster, increasing the current, but it reaches a limiting value In reality, not all electrons make it to the anode when there is no voltage (no E field accelerating charge) → some voltage is needed to push the photoelectrons across

Measuring maximum kinetic energy of the photoelectrons

Use ammeter to measure photoelectric current

We slowly increase the V (make it more negative) until current = 0

That is V stopping

Quantitative data on the photoelectric effect

If we plot Kmax vs frequency of incident light (SI units), the gradient is plank’s constant

• Gradient is only Planck’s constant if it is in SI units, and the y-axis is energy

• If Y-axis is voltage/potential difference, just multiply it by 1.602x10-19 to get W=qV

Then using y=mx+b, we get the equation: Kmax=hf-ϕ

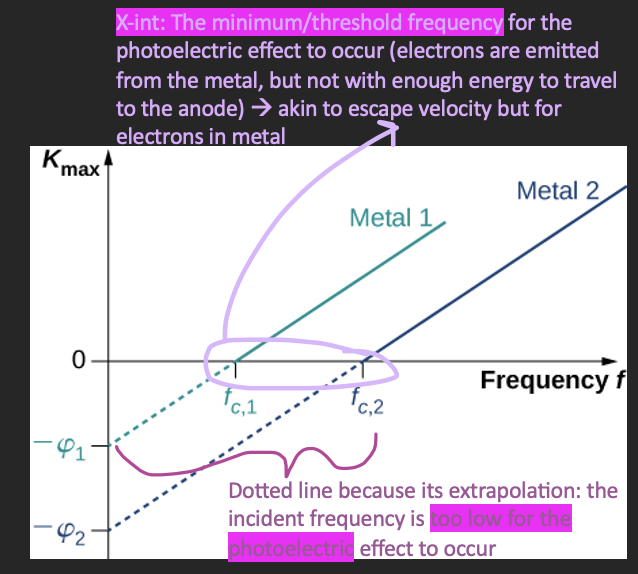
The work function

the minimum energy with which an electron is bound in the metal

• Different for each metal

• Can be determined if:

  • We know the y-intercept → ϕ is the y-int

  • We know the threshold frequency (x-intercept)

• Light at the threshold frequency gives just enough energy for electrons to overcome the work function

• It is free from the atom, but doesn’t have enough energy to jump off the metal

If f = f0, then Kmax = 0 → hf0 = ϕ

• Any leftover energy after overcoming the work function becomes kinetic energy