Chapter 3: Crystal Structure and Crystallography

Short Range v. Long Range Order

No order: Monoatomic gases

Short range order (SRO): mostly liquids

Long range order (LRO): metals and alloys

If a crystalline material consists of only one large crystal, we refer to it as a single crystal

Crystal Structure

• Solid materials may be classified according to the regularity with which atoms or ions are arranged wrt one another

• A crystalline material is one in which the atoms are situated in a repeating or periodic array over large atomic distances; that is, long-range order exists such that upon solidification, the atoms will position themselves in a repetitive 3D pattern, in which each atom is bonded to its nearest-neighbour atoms

• Some of the properties of crystalline solids depend on the crystal structure of the material, the manner in which atoms, ions, or molecules are spatially arranged

• The atomic order in crystalline solids indicates that small groups of atoms form a repetitive pattern. Thus, in describing crystal structures, it is often convenient to subdivide the structure into small repeat entities called unit cells.

• Thus, the unit cell is the basic structural unit or building block of the crystal structure and defines the crystal structure by virtue of its geometry and the atom positions within

Unit Cells

In describing crystal structures, it is often convenient to subdivide the structure into small repeat entities called unit cells.

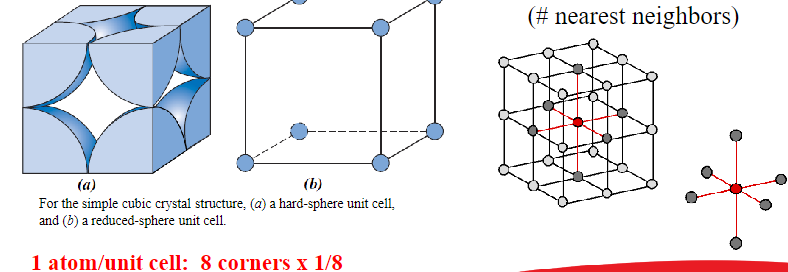
Simple Cubic Structure (SC)

• Rare due to low packing density (only Polonium has this structure)

• Close packed directions are cube edges

• Coordination number = 6

• APF: 0.52

• R = 0.5a

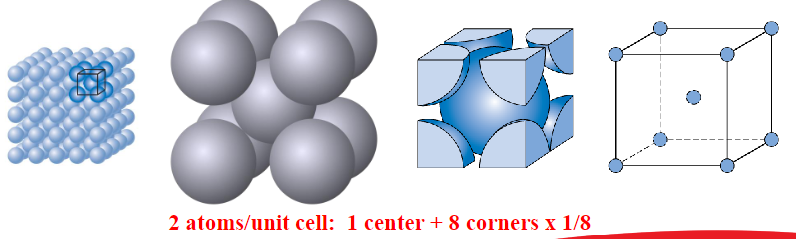
Body Centred Cubic (BCC)

• Atoms touch each other along cube diagonals

• Eg: Cr, W, Fe, Tantalum, Molybdenum

• Coordination number = 8

• APF: 0.68

• 4R = (sqrt3)a

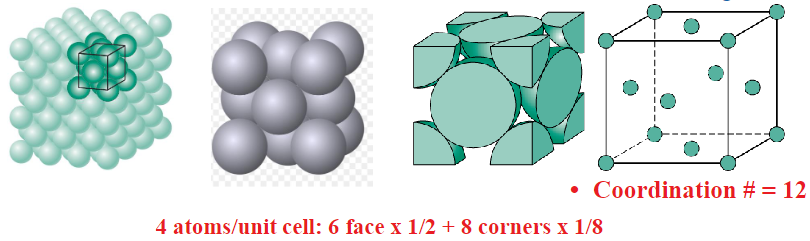
Face Centred Cubic (FCC)

• Atoms touch each other along face diagonals

• Eg: Al, Cu, Au, Pb, Ni, Pt, Ag

• Coordination number = 12

• APF: 0.74

• 4R = (sqrt2)a

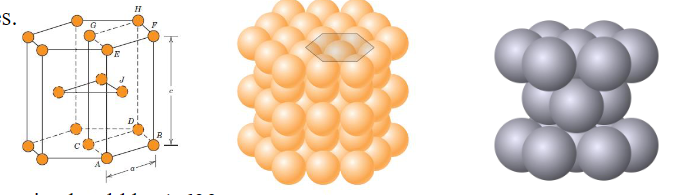
Hexagonal Closed-packed Structure (HCP)

• The top and bottom faces of the unit cell consist of six atoms that form regular hexagons and surround a single atom in the centre

• Another plane that provides three additional atoms to the unit cell is situated between the top and bottom planes

• c/a ratio should be 1.633

Atomic Packing Factor

APF = Volume of atoms in unit cell/volume of unit cell

*assume hard spheres

APF = (atoms/unit cell)(4/3)(P)(R³)/a³

Stacking Sequence

• FCC: ABCABC stacking sequence

• HCP: ABAB stacking sequence

Theoretical Density, ρ

Density = ρ = (mass of atoms in unit cell)/(total volume of unit cell)

ρ = nA/V_CN_A

n = number of atoms/unit cell

A = atomic weight

V_C = volume of unit cell = a³ for cubic

N_A = Avogadro’s number = 6.022x10²³ atoms/mol

Single Crystal

• For a crystalline solid, when the periodic and repeated arrangement of atoms is perfect or extends throughout the entirety of the specimen without interruption, the result is a single crystal

• Single crystals exist in nature, but they may also be produced artificially. They are ordinarily difficult to grow, because the environment must be carefully controlled

• Within the past few years, single crystals have become extremely important in many of our modern technologies, in particular electronic microcircuits, which employ single crystals of silicon and other semiconductors

• Properties vary with direction (anisotropic)

• Example: the modulus of elasticity in BCC iron

Polycrystals

• Most engineering materials are polycrystals

• Properties may or may not vary with direction

• If grains are randomly oriented - will not vary with direction (isotropic)

• If grains are textured - will vary with direction (anisotropic)

Anisotropic

Properties vary with direction.

Isotropic

Properties do not vary with direction.

Polymorphism

Two or more distinct crystal structures for the same material

Also called allotropy

Sometimes varies with temperature (titanium = HCP for low temp, and BCC for high, iron goes from BCC to FCC to BCC when increased to high temps)

Crystallographic Directions and Planes

• Deformation under loading (slip) occurs on certain crystalline planes and in certain crystallographic directions. Before we can predict how materials fail, we need to know what modes of failure are more likely to occur

• Other properties of materials (electrical conductivity, thermal conductivity, elastic modulus) can vary in a crystal with orientation

Lattice Directions, Planes, and Miller Indices

• Miller indices used to express lattice planes and directions

• x, y, z are the axes (on arbitrarily position origin)

• a, b, c are lattice parameters (length of unit cell along a side)

• h, k, l are the Miller indices for planes and directions - expressed as planes: (uvw) and direction: [uvw]

• Family of direction is represented by <uvw>

  • [100], [010], [001] are same family <100> cubic system

• Convention for naming: NO COMMAS bw numbers

How to Define Direction

• Crystallographic direction is represented by a vector connecting two points in the concerned direction

• The vector is shifted so that one end falls at the origin

• Vector projections on 3 axes are measured

• They are revised to the smallest integer ratio

• Now, the three indices measured is represented as [uvw], this is the direction

Miller Indices for Directions

• Draw vector, define tail as origin

• Determine length of the vector projection in unit cell dimensions, a, b, and c

• Remove fractions by multiplying by the smallest possible factor

• Enclose in square brackets

Families of Direction

HCP Crystallographic Directions

• The three a1, a2, and a3 axes are all contained within a single plane (called the basal plane) and are at 120 to one another

• The z axis is perpendicular to this basal plane. Directional indices, which are obtained as described earlier, will be denoted by four indices as [uvtw]

• By convention, the first three indices pertain to projections along the respective a1, a2, and a3 axes in the basal plane

Hexagonal Crystals - Miller-Bravais

4 parameter Miller-Bravais lattice coordinates are related to the direction indices as follows:

[u’v’w’] → [uvtw]

u = (1/3)(2u’ - v’)

v = (1/3)(2v’ - u’)

t = -(u + v)

w = w’

Miller Indices for Planes

• Similar to directions, unit cell based 3 axis coordinate system is used for planes too

• 3 miller indices (hkl) used for cubic system and 4 indices (hkil) used for HCP system

• Parallel planes are equivalent and has same miller indices

• Family of planes represented by {hkl}

• For a cubic system, if a plane and direction have the same set of miller indices, they are perpendicular to each other

Bracket Convention

Direction [uvw]

Direction Family <uvw>

Plane (hkl)

Plane Family {hkl}

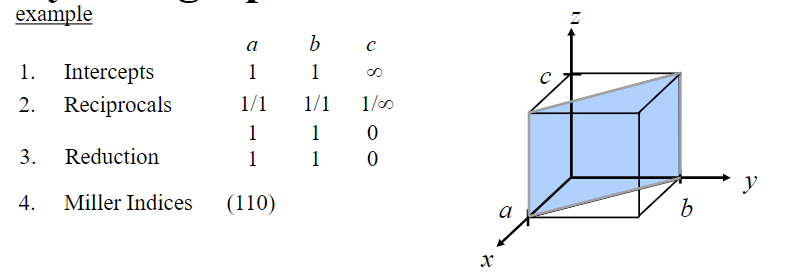
Miller Indices Procedure for Planes

Miller Indices: reciprocals of the three axial intercepts for a plane, cleared of fractions and common multiples. All parallel planes have the same Miller indices.

Algorithm

1. Read off intercepts of plane with axes in terms of a, b, c

2. Take reciprocals of intercepts

3. Reduce to smallest integer values

4. Enclose in parentheses, no commas

Slip Systems

Slip system is a combination of:

• Plane (hkl) with highest PD

• Direction [uvw] with highest LD lying in the plane

Linear and Planar Density

• Properties in general, depend on linear and planar density

• Examples:

  • Speed of sound along directions

  • Slip (deformation in metals) depends on linear and planar density

  • Slip occurs on planes that have the greatest density of atoms in direction with highest density

    • We would along closest packed directions on the closest packed planes

Atomic Densities

Linear Density:

• number of atoms per length whose centres lie on the direction vector for a specific crystallographic direction

• Linear Density = number of atoms centred on direction vector/length of direction vector

Planar Density:

• Number of atoms per unit area that are centred on a particular crystallographic plane

• Planar Density = number of atoms centred on a plane/area of the plane

X-Ray Diffraction

• Can be used to determine crystal structure

  • Identify unknown materials

  • Measure lattice parameters

• X-rays are a form of electromagnetic radiation that have high energies and short wavelengths

• Diffraction occurs whenever a wave encounters a series of regularly spaced obstacles that

  • Can scatter the wave

  • Have spacing comparable to the wavelength

• X-ray wavelength (λ) ~ inter-atomic

• Other techniques such as neutron or electron diffraction can also be used

• Diffraction gratings must have spacings comparable to the wavelength of diffracted radiation

• Can’t resolve spacing < λ

• Spacing is the distance between parallel planes of atoms

Interplanar Spacing

• Magnitude of the distance between two adjacent and parallel planes of atoms

• It is a function of the Miller indices (hkl) as well as the lattice parameters

• For example, for crystal structures that have cubic symmetry: d_hkl=a/(sqrt(h²+k²+l²)) in which a is the lattice parameter (unit cell edge length)

X-Rays to Determine Crystal Structure