CSE 311

CSE 311 Flashcards

Propositions

A statement that has a truth value (i.e. is true or false) and is “well-formed”. Can be clearly false so long as it is well-formed “Complete sentence”.
Ex: All cats are mammals (True, and a propositon)

Implications

A way to connect propositions. 𝑝 → 𝑞 and 𝑞 → 𝑝 are different implications!

An implication is false exactly when you can demonstrate I’m lying. This is why vacuous truth exists because you cant demonstrate a scenario that doesnt exist.

p → q Wordings:
-p implies q

-whenever p is true q must be true

-if p then q

q if p

-p is sufficient for q

-p only if q

-q is necessary for p

Order of Operations for Logic

Within a level, apply from left to right

1. Parentheses

2. Negation

3. And

4. Or, exclusive or

5. Implication

6. Biconditional  s

Logical Connectives

Negation (not) ¬𝑝
Conjunction (and) 𝑝 ∧ 𝑞
Disjunction (or) 𝑝 ∨ 𝑞
Exclusive Or 𝑝 ⊕ 𝑞
Implication(if-then) 𝑝 ⟶ 𝑞
Biconditional 𝑝 ⟷ q

Biconditonals

A two way implication. Think: (𝑝 → 𝑞) ∧ (𝑞 → 𝑝) is the same as 𝑝 ⟷ q

Wording:
p if and only if q
p iff q
p is equivalent to q
p implies q and q implies p
p is necessary and sufficient for q

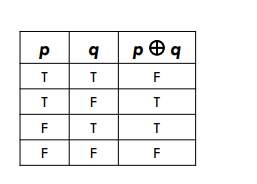
Exclusive Or

Exactly one of the two is true.
𝑝 ⊕ 𝑞

English wording:
“either 𝑝 or 𝑞” is the most common, but be careful. Often translated “𝑝 or 𝑞” where you’re just supposed to understand that exclusive or is meant (instead of the normal inclusive or).

Writting in own proofs:
Try to say either… or…

Demorgan’s law

Negates statements. 
¬ 𝑝 ∨ 𝑞 ≡ ¬𝑝 ∧ ¬𝑞 
¬ 𝑝 ∧ 𝑞 ≡ ¬𝑝 ∨ ¬q

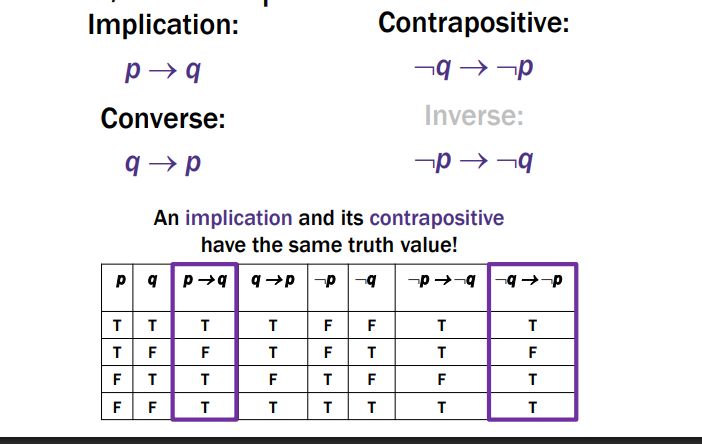
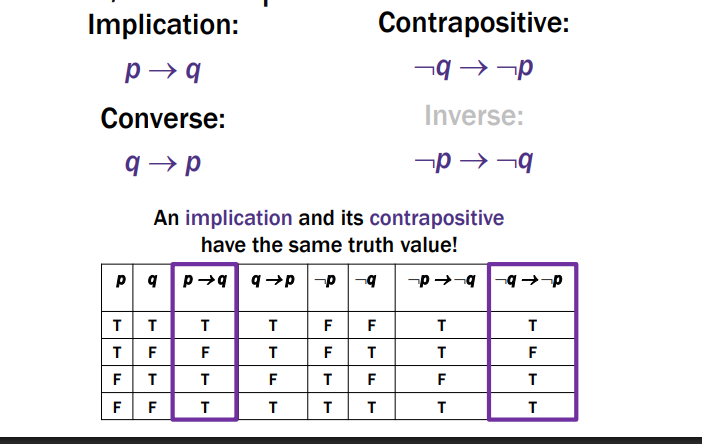
Contrapositive Vs. Implication VS Converse Vs Inverse

Contrapositive and Implication have the same truth values so they are equivalent.

Inverse and Converse have same truth value

Ex:
Implication: If it’s raining, then I have my umbrella. p → q

Contrapositive: If I don’t have my umbrella, then it is not raining ¬q → ¬p

Tautology VS Contradiction VS Contingency

Tautology: A proposition that is always true. 

Contradiction: A proposition that is always false

Contingency: A proposition that can be both true and false.

Examples:

𝑝 ∨ ¬𝑝
Tautology
If 𝑝 is true, 𝑝 ∨ ¬𝑝 is true; if 𝑝 is false, 𝑝 ∨ ¬𝑝 is true.

𝑝 ⊕ p
Contradiction
If 𝑝 is true, 𝑝 ⊕ 𝑝 is false; if 𝑝 is false, 𝑝 ⊕ 𝑝 is false.

(𝑝 → 𝑞) ∧ p
Contingency
If 𝑝 is true and 𝑞 is true, 𝑝 → 𝑞 ∧ 𝑝 is true;
If 𝑝 is true and 𝑞 is false, 𝑝 → 𝑞 ∧ 𝑝 is false.

Digital Circuits

Simply another way to represent propositional

values get song along wires connecting gates

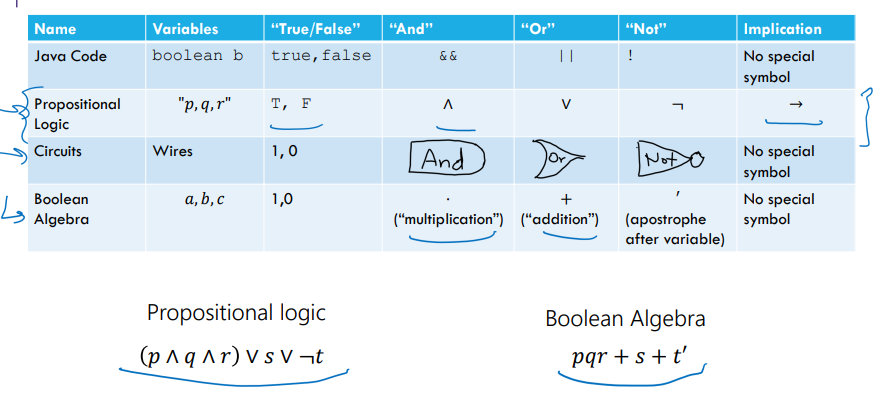
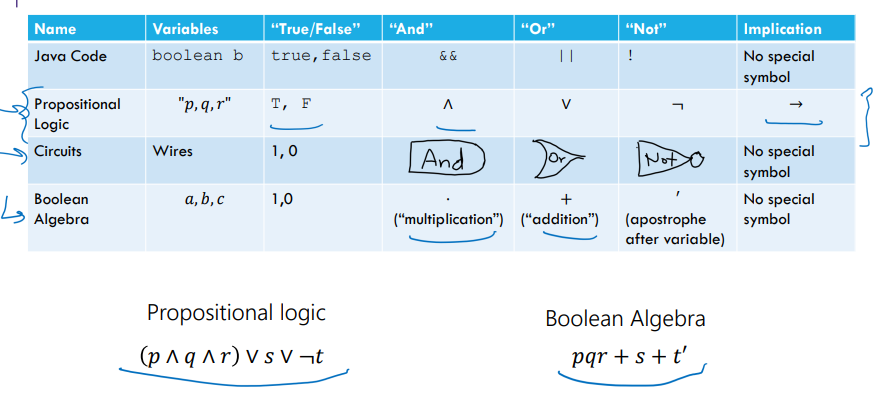
Boolean Algebra/Propositional Logic/ Circuits Syntax

Boolean Algebra Explanation:
Preferred by some mathematicians and circuit designers. “or” is + “and” is ⋅ (i.e. “multiply”) “not” is ‘ (an apostrophe after a variable)

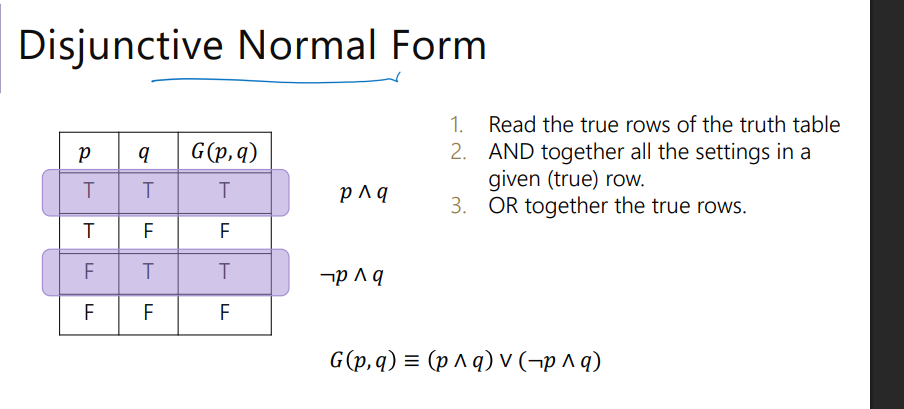
Disjunctive Normal Form (OR of ANDs)

1. Read the true rows of the truth table

2. AND together all the settings in a given (true) row.

3. OR together the true rows

Conjunctive Normal Form (AND of ORS) 

1. Read the false rows of the truth table

2. OR together the negations of all the settings in the false rows.

3. AND together the false rows.

Predicates

A function that outputs true or false.

Domain of Discourse

The set of all inputs allowed as inputs to our predicates.

Universal Quantifier

“∀𝑥“
“for each 𝑥”, “for every 𝑥”, “for all 𝑥” are common translations
Remember: upside-down-A for All.

Existential Quanitifier

“∃𝑥“
“there is an 𝑥”, “there exists an 𝑥”, “for some 𝑥” are common translations Remember: backwards-E for Exists.

Negating Quantifiers

To negate an expression with a quantifier
1. Switch the quantifier (∀ becomes ∃, ∃ becomes ∀)
2. Negate the expression inside

Arbitrary Values

An “arbitrary” variable is one that is part of the domain of discourse (or some sub-domain you pick). You know nothing else about.
EVERY element of the domain could be plugged into that arbitrary variable. And everything else you say in the proof will follow.

If you want to prove a for-all you must explicitly tell us the variable is arbitrary when it is introduced

Direct Proof Steps.

These are the usual steps. We’ll see different outlines in the future!!

• Introduction

• Declare an arbitrary variable for each ∀ quantifier

• Assume the left side of the implication

• Core of the proof

•Unroll the predicate definitions

• Manipulate towards the goal (using creativity, algebra, etc.)

• Reroll definitions into the right side of the implication

• Conclude that you have proved the claim

How to translate:

1. "All P's are Q's"

2. "Some P is a Q"

• ∀x(P(x) → Q(x))

  • Rule: Universal (∀) is paired with an Implication (→).

• ∃x(P(x) ∧ Q(x))

  • Rule: Existential (∃) is paired with a Conjunction (∧).

De Morgan's Laws

1. Propositions (∧, ∨)

2. Quantifiers (∀, ∃)

• Propositions:

  • ¬(P ∧ Q) ≡ ¬P ∨ ¬Q

  • ¬(P ∨ Q) ≡ ¬P ∧ ¬Q

• Quantifiers:

  • ¬∀x P(x) ≡ ∃x ¬P(x)

  • ¬∃x P(x) ≡ ∀x ¬P(x)

  • Rule: Flip the quantifier and push the negation in.

What is the...

1. Negation of P → Q? (Opposite)

2. Contrapositive of P → Q? (Equivalent)

• Negation: ¬(P → Q) ≡ P ∧ ¬Q

  • "The 'if' part is true AND the 'then' part is false."

• Contrapositive: (P → Q) ≡ (¬Q → ¬P)

  • "If not Q, then not P."

  • Key: Contrapositive only applies to implications and does not flip quantifiers.

How to derive DNF and CNF from a truth table?

• DNF (Disjunctive Normal Form): "OR of ANDs"

  1. Find all rows where OUT = TRUE.

  2. Write an ∧ (AND) clause for each T-row. (e.g., (p ∧ ¬q ∧ r))

  3. Combine all these ∧ clauses with ∨ (OR).

• CNF (Conjunctive Normal Form): "AND of ORs"

  1. Find all rows where OUT = FALSE.

  2. Write a ∨ (OR) clause for each F-row. (e.g., (¬p ∨ q ∨ ¬r))

  3. Combine all these ∨ clauses with ∧ (AND).

Front: Formal definitions for:

1. Even(x)

2. Odd(x)

• Even(x) ∶= ∃k (x = 2k) (for some integer $k$)

• Odd(x) ∶= ∃k (x = 2k + 1) (for some integer $k$)

How to prove:

1. ∀x(P(x) → Q(x))

2. ∃x P(x)

• To Prove ∀x(P(x) → Q(x)) (Direct Proof):

  • Let $x$ be an arbitrary integer.

  • Assume $P(x)$ is true.

  • Use definitions and algebra to...

  • ...Conclude that $Q(x)$ must be true.

• To Prove ∃x P(x) (Constructive Proof):

  • State a specific value for $x$ (e.g., "Let $x = 2$").

  • Show that $P(x)$ is true for that one value.

Front:

1. How to translate "A unless B"?

2. Logic Gate Symbols (NOT, AND, OR)

• "A unless B" translates to A ∨ B.

  • (Logically equivalent to ¬B → A)

• Logic Gates:

  • ¬ (NOT) = Triangle with circle ⊳○

  • ∧ (AND) = D-shaped symbol ⊲

  • ∨ (OR) = Curved, pointy symbol ⋓

How do you write a Direct Proof for a claim like ∀x(P(x) → Q(x))?

This is the "English proof" style:

1. Introduce Variable: "Let $x$ be an arbitrary integer." (This is for the ∀x).

2. Assume Hypothesis: "Suppose $P(x)$ is true." (This is for the →).

3. Work (Unroll, Manipulate): Use definitions (e.g., x = 2k), algebra, and logic to work from $P(x)$.

4. Show Conclusion (Reroll): Manipulate your expression until you can show that $Q(x)$ must be true (e.g., show the result is $2(\text{some integer})$).

5. Conclude: "Since $x$ was arbitrary, we have proven ∀x(P(x) → Q(x))."

How do you formally prove an implication A → B in an inference proof?

You start a subproof by assuming A and showing it leads to B. The rule lets you "discharge" the assumption.

Structure:

k.1. A (Assumption)

... (logical steps)

k.m. B (...)

k+1. A → B (Direct Proof Rule, using lines $k.1\text{--}k.m$)

• Lines inside the subproof are indented.

• The final fact, A → B, is not indented; it's an unconditional fact.

What do "arbitrary" and "fresh" mean for quantifier rules?

• Arbitrary (for Intro ∀):

  • An "arbitrary" $a$ is one you know nothing about.

  • You get an arbitrary variable by saying "Let $a$ be arbitrary" or by using Elim ∀.

  • BUG: You cannot use Intro ∀ on a variable that came from Elim ∃ (it's not arbitrary, it's a specific, "fresh" value).

• Fresh (for Elim ∃):

  • A "fresh" $c$ is a brand new variable that has not appeared anywhere else in the proof.

  • BUG: A variable is not "arbitrary" if it depends on another variable (e.g., $b = a+1$). You cannot use Intro ∀ on such a variable (this is the ∀x∃y vs. ∃y∀x bug).

What is the formal definition of "x divides y"? (Notation: $x | y$)

For integers $x, y$:

$x | y$ if and only if there is an integer $z$ such that $xz = y$.

• Examples:

  • 2 | 4 is True (let $z=2$)

  • 4 | 2 is False (no integer $z$)

  • 5 | 0 is True (let $z=0$)

  • 0 | 5 is False (no integer $z$)

  • 1 | 5 is True (let $z=5$)

What is The Division Theorem? (Hint: quotient and remainder)

For every integer $a$ and positive integer $d$, there exist unique integers $q$ and $r$ such that:

$a = dq + r$

and $0 \le r < d$

• $q$ is the quotient (like a / d in Java)

• $r$ is the remainder (like a % d in Java, but always non-negative)

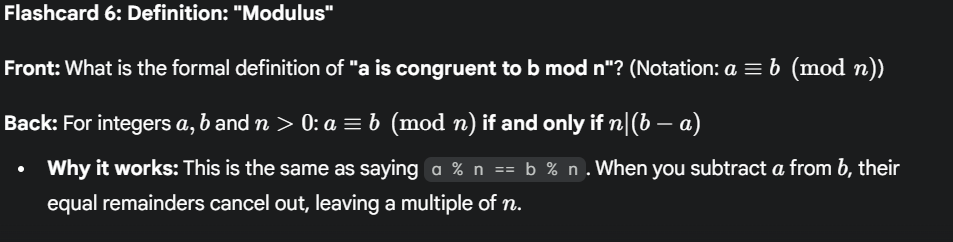
What is the formal definition of "a is congruent to b mod n"? (Notation: a == b mod{n}

For integers a, b and n > 0:

a == b mod{n} if and only if n | (b - a)

• Why it works: This is the same as saying a % n == b % n. When you subtract a from b, their equal remainders cancel out, leaving a multiple of n.

If a == b mod{n}, what is true about:

1. a + c ?

2. ac?

3. b == a mod{n} ?

Modular congruence behaves like equality:

1. Addition: a + c == b + c mod{n}

2. Multiplication: ac == bc mod{n}

3. Symmetry: b == a mod{n} is also true.

How do you prove a ∀x P(x) (universal) statement is FALSE?

By finding a counterexample. This is a constructive proof of the negation, ∃x ¬P(x).

Steps:

1. State your specific value: "Consider $x = 6$."

2. Show it fails: "We must show Even(x) ∧ ¬(8 | x^2)."

3. Prove it: "$x=6$ is even. $x^2 = 36$. $8$ does not divide $36$, since $36 = 8 \times 4 + 4$.

What is the strategy for a Proof by Cases?

Use this when your assumption gives you an "OR" condition (e.g., $x$ is even or $x$ is odd).

1. State your cases: "We divide into two cases."

2. Case 1: "Case 1: $x$ is even."

   • ... (prove the claim for this case)

3. Case 2: "Case 2: $x$ is odd."

   • ... (prove the claim for this case)

4. Conclusion: "Since the claim holds in all exhaustive cases, the claim is true.

How do you prove these properties for a == b mod{n}?

1. Addition: a+c == b+c mod{n}

2. Multiplication: ac == bc mod{n}

Both proofs start by assuming $a == b mod{n}, which means n | (b - a), so nk = b - a for some integer k.

1. Addition:

   • By algebra, nk = (b+c) - (a+c).

   • Since k is an integer, n | ((b+c) - (a+c)).

   • By definition of mod, a+c == b+c mod{n}.

2. Multiplication:

   • Multiply the equation by c: n(kc) = bc - ac.

   • Since k and c are integers, kc is an integer.

   • Thus, n | (bc - ac).

   • By definition of mod, ac == bc mod{n}.

What do these statements mean intuitively?

• x ≡ 0 (mod 2)

• a ≡ b (mod n)

• y ≡ 2 (mod 7)

• x ≡ 0 (mod 2) means "x is even."

• a ≡ b (mod n) means "a and b have the same remainder when divided by n." (i.e., a % n == b % n)

• y ≡ 2 (mod 7) means "y is 2 more than a multiple of 7." (i.e., $y = 7k + 2$ for some integer $k$)

How do you disprove a universal statement like ∀x P(x)?

By Proof by Counterexample.

This is a constructive proof of the negation, ∃x ¬P(x).

Steps:

1. State your specific value: "Consider $x = c$."

2. Show it fails: Prove that ¬P(c) is true for that $c$.

   • Example: To disprove ∀x (Even(x) → 8 | x²), use $x = 6$.

   • Proof: $6$ is even, but $6^2 = 36$, and ¬(8 | 36) (since $36 = 8 \cdot 4 + 4$).

What is the strategy for a Proof by Cases?

Use this when your assumption can be broken into a set of exhaustive (all-covering) cases. (e.g., $x$ is even or $x$ is odd; $x > 0$ or $x < 0$ or $x = 0$).

Steps:

1. State your cases: "We divide into two cases: Case 1 ($x$ is even) and Case 2 ($x$ is odd)."

2. Prove the claim for Case 1.

3. Prove the claim for Case 2.

4. Conclude: "Since the claim holds in all exhaustive cases, the original claim is true."

What is Proof by Contrapositive? When should you use it?

• Technique: To prove P → Q, you prove the logically equivalent contrapositive ¬Q → ¬P instead.

• Steps:

  1. State you are proving by contrapositive.

  2. Write the contrapositive statement.

  3. Assume ¬Q (the new hypothesis).

  4. Use a direct proof to show ¬P (the new conclusion).

• When to use:

  1. The hypothesis P has a "not" (e.g., a ∤ b).

  2. The conclusion Q has an "OR" or "not" (e.g., a ∤ b ∨ a ∤ c).

What are the definitions of:

• GCD(a, b)

• LCM(a, b)

• GCD(a, b) (Greatest Common Divisor):

  The largest integer $c$ such that $c | a$ AND $c | b$.

• LCM(a, b) (Least Common Multiple):

  The smallest positive integer $c$ such that $a | c$ AND $b | c$.

What is the code/logic for the Euclidean Algorithm to find gcd(m, n)?

repeatedly uses the fact that gcd(m, n) = gcd(n, m % n).


// Assumes m >= n

while (n != 0)

{ int rem = m % n;

m = n; n = rem;

}

return m; // m holds the last non-zero remainder

Front: Define the following symbols/terms:

1. Set

2. Size of A

3. a ∈ A

4. A ⊆ B

5. A = B

• Set: An unordered group of distinct elements.

• Size of A: The cardinality (size) of set A.

• a ∈ A: "a is an element of A."

• A ⊆ B (Subset): Every element of A is also in B.

  • Logic: ∀x (x ∈ A → x ∈ B)

• A = B (Equality): A and B have identical elements.

  • Logic: A ⊆ B ∧ B ⊆ A (or ∀x (x ∈ A ↔ x ∈ B))

Foundational Set Definitions

Define the following:

Front: Define the following:

1. Set-Builder Notation

2. A ∈ P(B)

3. A ⊆ B (Logic)

4. A = B (Proof Rule)

• Set-Builder Notation: A way to define a set by stating the properties its elements must satisfy.

  • Form: { variable : conditions }. (e.g., {x : x ∈ Z ∧ x % 2 = 0})

• A ∈ P(B) (Powerset): "A is an element of the power set of B," which means A is a subset of B (A ⊆ B).

• A ⊆ B (Subset Logic): ∀x (x ∈ A → x ∈ B)

• A = B (Proof Rule): Show A ⊆ B AND B ⊆ A.

Set Operations (Using set-builder)

Define the following set operations using Set-Builder Notation:

1. Union (A ∪ B)

2. Intersection (A ∩ B)

3. Complement (Aᶜ)

4. Difference (A \ B)

5. Cartesian Product (A × B)

• A ∪ B = {x : x ∈ A ∨ x ∈ B}

• A ∩ B = {x : x ∈ A ∧ x ∈ B}

• Aᶜ = {x : x ∈ 𝒰 ∧ x ∉ A} (Where 𝒰 is the Universe)

• A \ B = {x : x ∈ A ∧ x ∉ B}

• A × B = {(a, b) : a ∈ A ∧ b ∈ B} (Set of all ordered pairs)

Proof Skeletons (Set Proofs)

Give the full proof skeleton for:

1. Showing A ⊆ B (Subset)

2. Showing A = B (Equality)

• To Show A ⊆ B (Subset Proof):

  • "Let x be an arbitrary element of A."

  • (Use definitions/logic/equivalences to show x ∈ B.)

  • "Since x was an arbitrary element of A, A ⊆ B."

• To Show A = B (Equality Proof):

  • Part 1: Show A ⊆ B.

  • Part 2: Show B ⊆ A.

  • Conclusion: "Since the subset relation holds in both directions, A = B."

Recursive Set Definitions

1. What are the two components of a Recursive Set Definition?

2. Write the recursive definition for the set of Natural Numbers (N) ≥ 0.

• Recursive Set Components:

  • Basis Step: Specifies the initial element(s).

  • Recursive Step: Provides a rule for generating new elements from existing ones.

• Natural Numbers (N):

  • Basis Step: 0 ∈ S

  • Recursive Step: If x ∈ S, then x + 1 ∈ S.

The Principle of Induction (The Domino Analogy)

What is the principle of induction?

Its a proof technique to show that a predicate P(n) is true for all natural numbers n >= 0. 

You must prove two things: 
1. P(0) is true. (You knock over the first domino).
2. ∀k (P(k) → P(k+1)) is true. (You must show that for any domino, if it falls, it will knock over the next one).

Formal Rule: [P(0) ∧ ∀k(P(k) → P(k+1))] → ∀n P(n)

Weak Induction Proof’s Skeleton

What is the 5-step skeleton for an English proof by induction?

What is the 5-step skeleton for an English proof by induction?
1. Define P(n): “Let P(n) be the predicate ‘…’. We will prove ∀n P(n) by induction on .
2. Base Case: “We show P(0/Base case) is true. …” (Do the algebra to show the statement holds for n = 0 / n = base case).
3. Inductive Hypothesis (IH): “Assume P(K) is true for an arbitrary integer k>= 0. “ (This line is just stating the assumption).

4. Inductive Step (IS): “We want to show P(K+1) is true. i.e p(k) → p(k + 1)” (This is the main work. You MUST state where you use the IH).

5. Conclusion: “Therefore, P(n) holds for all n >= 0 by the principle of induction”.

Induction Proof Strategies (Summations & Code)

What is the key strategy for the Inductive Step (IS) when proving…

1. Summations (like Σ...)?
2. Recursive Code?

1. For Summations (Σ):

   • Break off the last term

   • Example: Σ(i=0 to k+1) = [ Σ(i=0 to k) ] + (the (k+1)th term)

   • Then, use the inductive Hypothesis (IH) on the [ Σ(i=0 to k) ] part.

   • Use algebra to simplify the result into the gaol form for P(K+1).

2. For Recursive Code:

   1. Trace the code with input k+1. It will go to the else (recursive) branch.

   2. This branch will call the function with input k.

   3. Use the IH to replace the recursive call function(k) with the value its supposed to return (what P(k) claims).

   4. Use algebra to show the final returned value matches the goal for P(K+1).

Key Induction Formula: Sum of Powers of 2

What is the formula for the sum of the first n powers of 2 (starting from 2^0)? 

Σ(i=0 to n) 2ⁱ = 1 + 2 + 4 + ... + 2ⁿ = 2ⁿ⁺¹ - 1

(Very common formula to prove using induction.)

Strong vs. Weak Induction (The Hypothesis)

What is the difference between a Weak and Strong inductive Hypothesis?

Weak Inductive Hypothesis (IH): You assume P(k) is true ( Just the previous singer step). Used when P(K+1) Depends only on P(K)

Strong Inductive Hypothesis (IH): You assume P(b) ∧ P(b+1) ∧ ... ∧ P(k) are all true (all steps from the base case b up to k). Used when P(k+1) depends on any smaller value, like P(k-3) or P(k/2).

Strong Induction Skeleton (Multiple Base Cases)

What is the 5-step skeleton for a Strong Induction proof that requires multiple base

• Define P(n): "Prove P(n) for all n >= b_min..."

• Base Cases: Show P(b_min), P(b_min + 1), ..., P(b_max) are all true.

• Inductive Hypothesis (IH): "Assume P(b_min) ∧ ... ∧ P(k) are all true for an arbitrary integer k >= b_max."

• Inductive Step (IS): "We want to show P(k+1) is true. ..." (Use the IH on one or more values <= k, e.g., P(k-3)).

• Conclusion: "Therefore, P(n) holds for all n >= b_min by the principle of induction."

Strong Induction: How Many Base Cases?

How do you know how many base cases you need for a strong induction proof?

You need enough base cases to ensure your Inductive Step is always valid.

Rule of Thumb: If your Inductive Step for P(k+1) refers back s steps (e.g., you use P(k-s+1)), you need s consecutive base cases.

Example: The "stamp problem" needs to prove P(k+1) using P(k-3) (a 4-cent stamp). This is a gap of 4 steps (k-3, k-2, k-1, k). You need 4 base cases: P(12), P(13), P(14), and P(15). Your IH can then assume k >= 15, and P(k-3) will always be valid.

Structural Induction (The Principle)

Front: What is the principle of Structural Induction?

Its a proof technique to show that a predicate p(x) is true for all elements x in a recursively defined set S.

You must prove two things:

1. Base cases(s): Prove P(b) is true for all elements in b in the Basis Step of S.

2. Inductive Step: Assume P(x), P(y), etc. (the "old" elements) are true. Use them to prove P is true for the "new" element built from them (e.g., prove P(x+y)).

Structural Induction (Formal 5-Step Skeleton)

What is the 5-step skeleton for a Structural Induction proof?

• Define P(x): "Let P(x) be '...'. We prove ∀x ∈ S by structural induction."

• Base Case(s): "Show P(b) is true for all basis elements b..."

• Inductive Hypothesis (IH): "Assume P(x), P(y), ... are true for arbitrary elements x, y, ... from the recursive step."

• Inductive Step (IS): "We want to show P(new_element). ..." (Use the IH on x, y, ... to prove it).

• Conclusion: "Therefore, P(x) holds for all x ∈ S by structural induction."

Recursive Definition: Strings (Σ*)

Front: What is the recursive definition of Σ* (the set of all strings over an alphabet Σ)?

• Basis Step: ε ∈ Σ* (The empty string, "", is in the set).

• Recursive Step: If w ∈ Σ* (an existing string) and a ∈ Σ (a character), then wa (the string w with a appended) is in Σ*.

Recursive Definitions (Strings & Trees)

Front: Give the recursive definitions for:

1. len(w) (String Length)

2. height(T) (Binary Tree Height)

3. size(T) (Binary Tree Size)

1. len(w) (String Length):

   • len(ε) = 0

   • len(wa) = len(w) + 1 (for w ∈ Σ*, a ∈ Σ)

2. height(T) (Binary Tree Height):

   • height(leaf) = 0

   • height(T_new) = 1 + max(height(T_Left), height(T_Right))

3. size(T) (Binary Tree Size):

   • size(leaf) = 1

   • size(T_new) = 1 + size(T_Left) + size(T_Right)

How is Weak Induction (over n ∈ ℕ) a special case of Structural Induction?

You can define the Natural Numbers ℕ recursively:

• Basis: 0 ∈ ℕ

• Recursive: If k ∈ ℕ, then k+1 ∈ ℕ

An induction proof on ℕ is just a structural induction proof on this set.

• Base Case: Prove P(0).

• Inductive Step: Assume P(k) (the "old" element) and use it to prove P(k+1) (the "new" element).