Pascal's Principle

Blaise Pascal

French mathematician who published treatise on the Equilibrium of Liquids, in 1653, laying foundations for the study of static fluids.

Static fluid

A fluid that is not in motion.

Static equilibrium of a fluid

Condition when a fluid is not flowing; the net force on any part of the fluid is zero.

Hydrostatic equilibrium

Static equilibrium specifically for water.

Pascal’s principle

A change in pressure applied to an enclosed fluid is transmitted undiminished throughout the fluid and to the container walls.

Implication of Pascal’s principle

The total pressure in a fluid is the sum of pressures from different sources (e.g., depth + atmospheric pressure).

Importance of Pascal’s observations

Provided the foundation for hydraulics

Hydraulics

A branch of mechanics that uses the principles of fluid pressure transmission (Pascal’s principle) to perform work, commonly applied in machines like brakes, lifts, and presses.

It states that a change in pressure applied to an enclosed fluid is transmitted undiminished to all parts of the fluid and to the container walls.

What is Pascal’s principle (Pascal’s law)?

Because the atoms of the fluid are free to move and transfer pressure throughout.

Why can pressure changes be transmitted in an enclosed fluid?

No, actual pressure varies with height, but any change in pressure is transmitted equally throughout the fluid.

Does Pascal’s principle mean pressure is the same at all points in a fluid?

It applies only to changes in pressure, not to the total pressure at different depths.

What is the key limitation of Pascal’s principle?

h

(1)

m

(2)

ptop

(3)

pbottom

(4)

Mg

(5)

ptop,new

(6)

pbottom,new

(7)

A

(8)

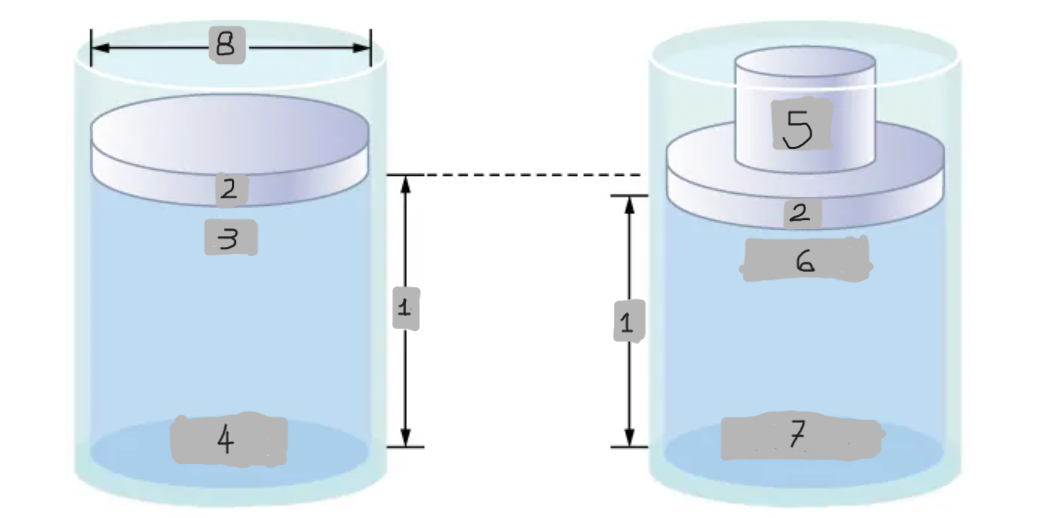
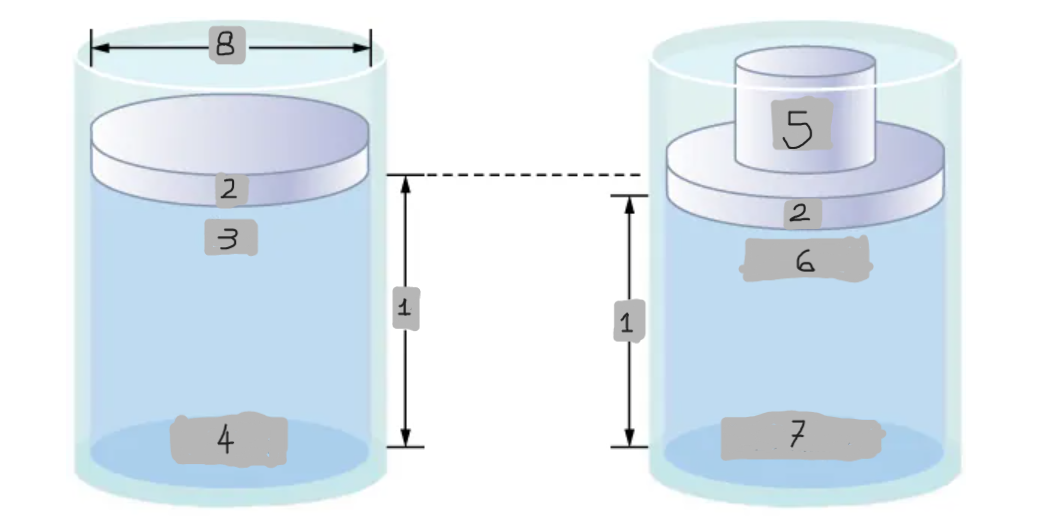
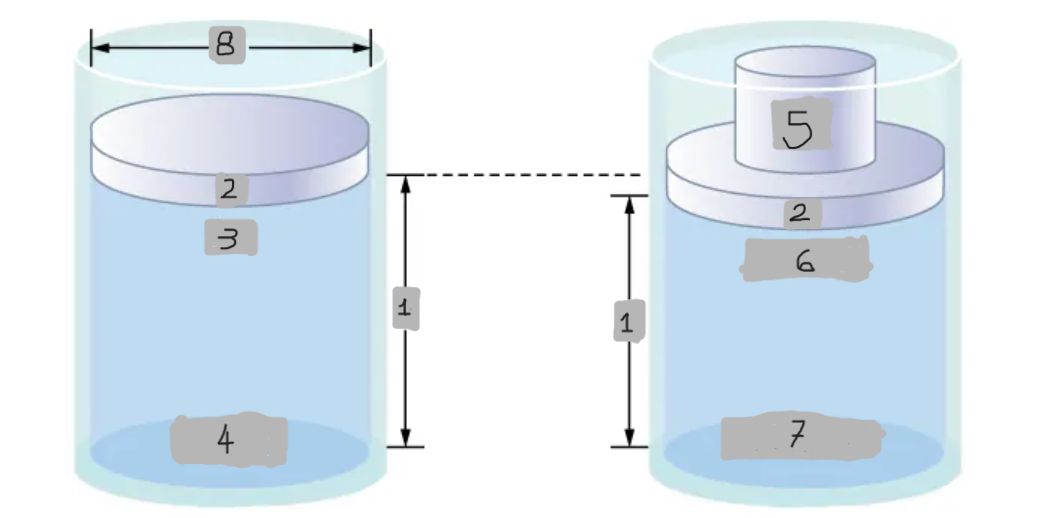
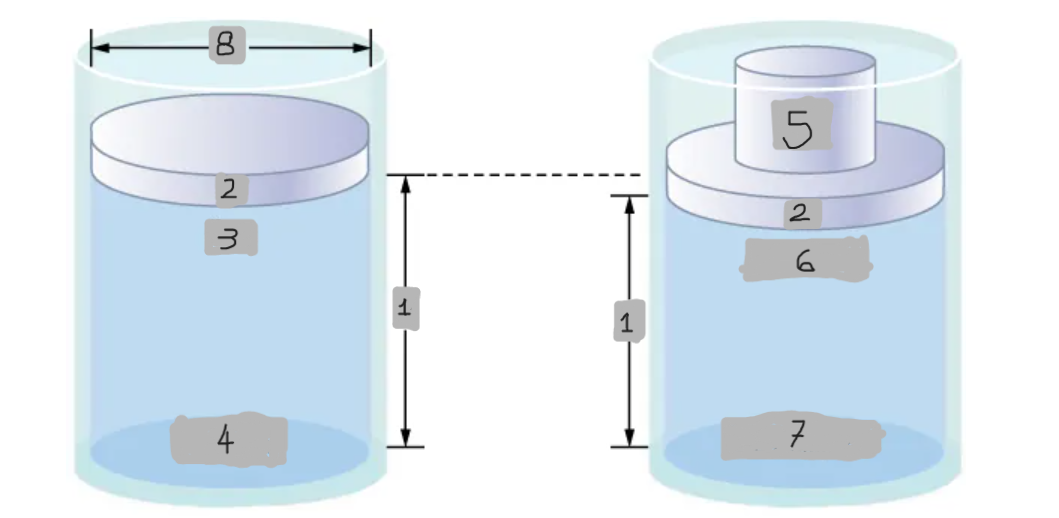
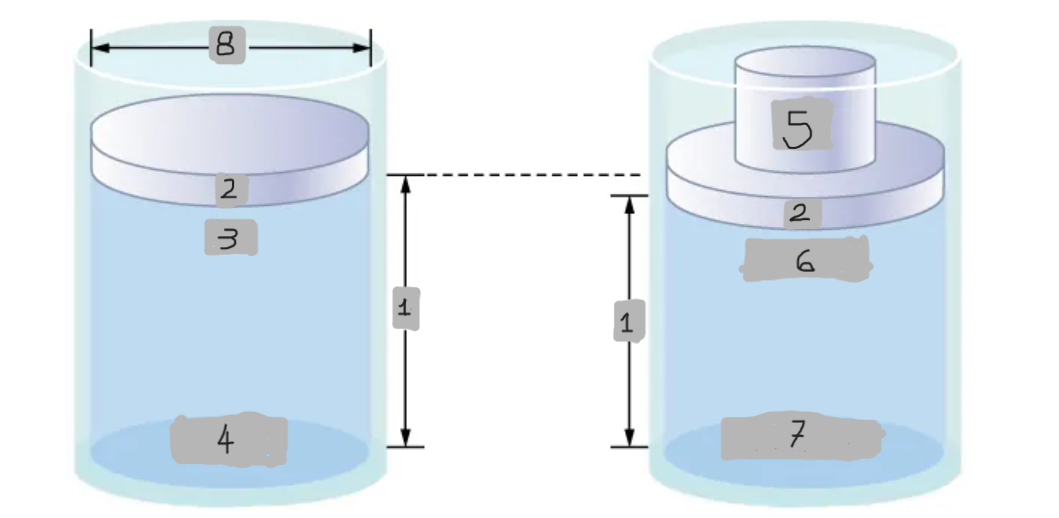
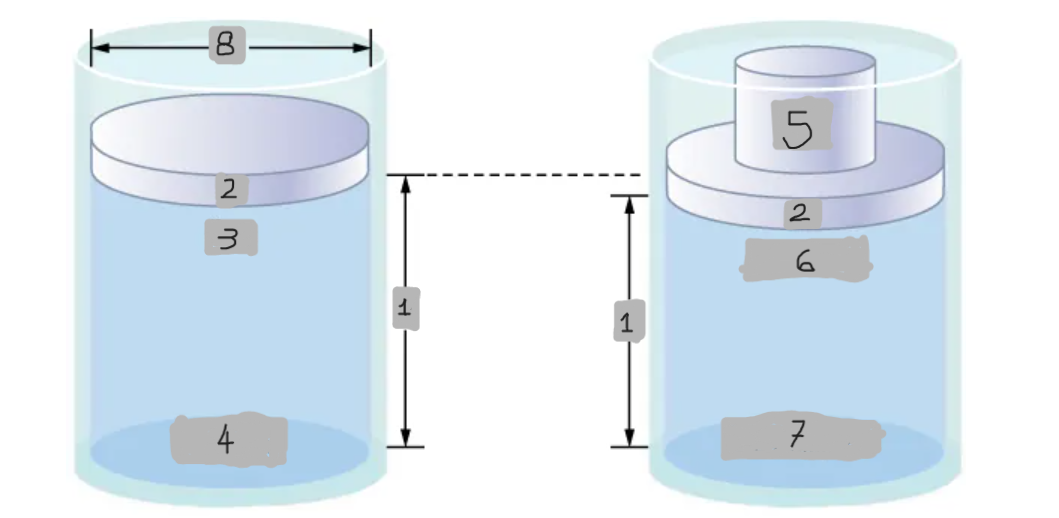
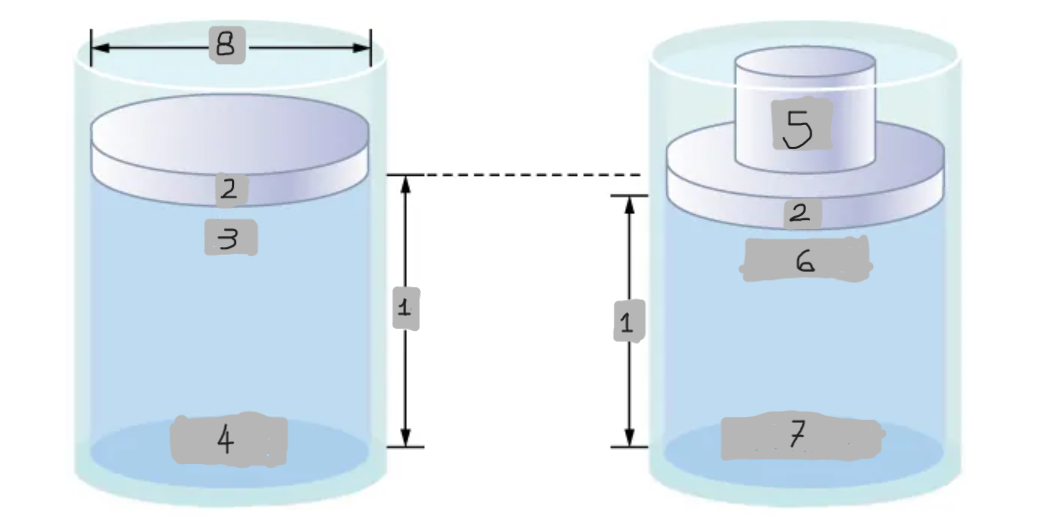
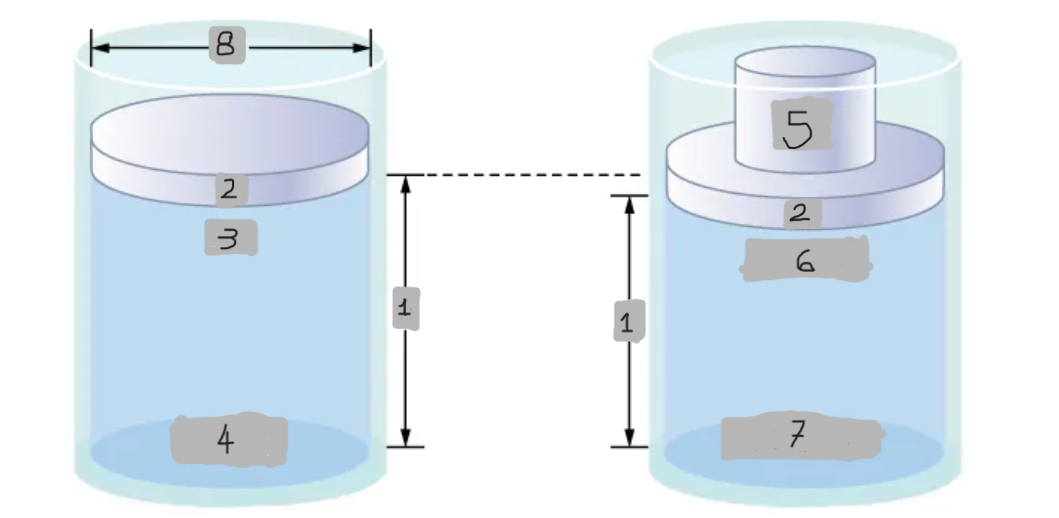
Pressure difference in a fluid column

Pressure at the top of the fluid is less than at the bottom due to the weight of the fluid.

Increases fluid pressure everywhere equally by (Mg/A)

Effect of adding mass to piston

pbottom = patm + pfluid + (Mg/A)

Pressure at the bottom with added mass

Δpbottom = (Mg/A)

Mathematical representation of the Pressure change at the bottom

Δp = Δptop = Δpbottom = Δpeverywhere

Mathematical representation of the Universality of pressure change (Pascal’s principle)