Chemistry I Lesson 9: Titrations Part I

What is the purpose of a titration?

To determine the concentration of a solution.

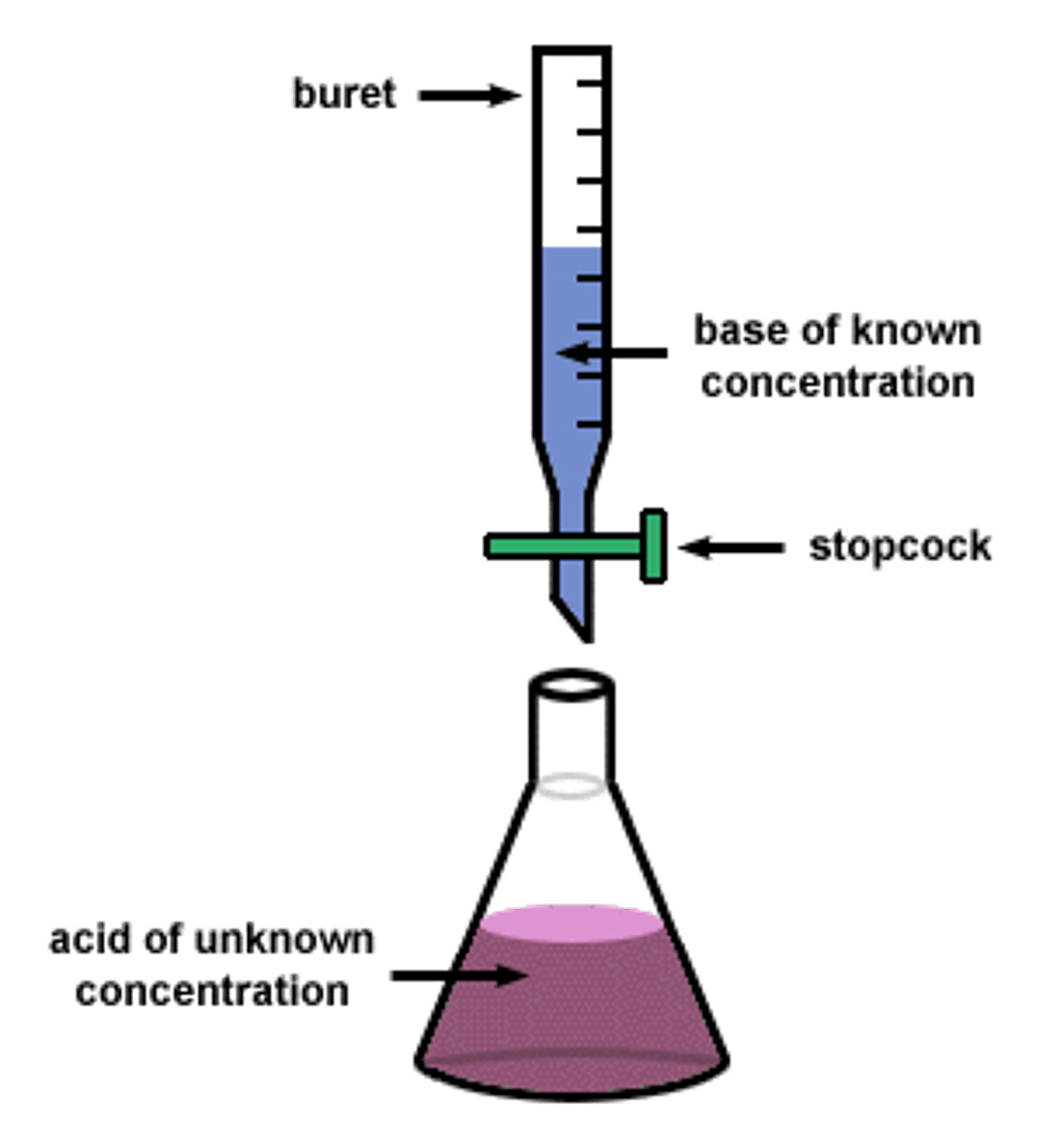
CRB True or false? At the equivalence point, there is no buffering capacity because the titrand (what the titrant is being added to) has fully reacted with the titrant.

True. At the equivalence point, there is no buffering capacity because the titrand (what the titrant is being added to) has fully reacted with the titrant.

Explain the relationship between an acid-base indicator (like phenolphthalein) and the end point of a titration?

The acid-base indicator will have specific pH where it changes color (phenolphthalein is colorless in acidic conditions and pink in basic conditions). At the end point of the titration, the acid-base indicator changes colors, showing that just enough reactant has been added to be equivalent to the acid/base present.

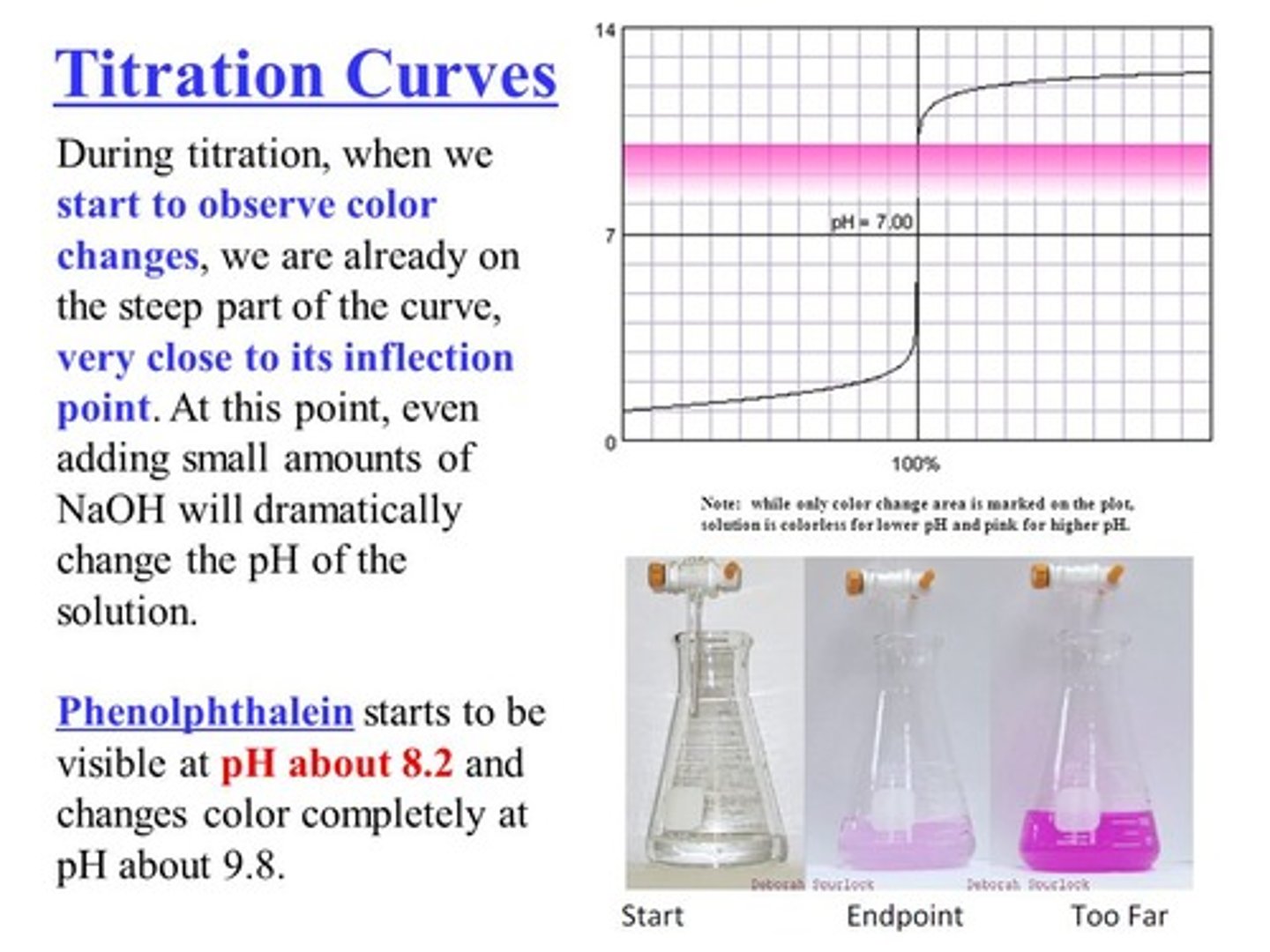
CRB Describe what would happen if the indicator was a stronger acid or base than the titrand being used.

If the indicator is a stronger acid or base than the titrand being used, then the first titrant that is added will react with the indicator instead of the titrand! This means you wasted a solution :(

CRB Explain the difference between the equivalence point and end point, focusing on the volume difference needed to achieve both.

The equivalence point is where all of the titrand has reacted, whereas the end point is later, once the titrant is reacting with the indicator. If you picked a good indicator though, the difference in volume should be negligible!

CRB Which of the following is a typical range from which the indicator will have a color change?

(A) pKa ± 10

(B) pKa ± 0.1

(C) pKa ± 3

(D) pKa ± 1

(D) pKa + or - 1

Generally, an indicator (like phenolphthalein) will have its color change within 1 pH unit of its pKa. This can vary based on the indicator though!

You have a solution of 453 mL of HCl. If it takes 46.3 mL of .287 M NaOH to reach the end point of our titration of the HCl solution, what is the concentration of HCl in the original solution?

(A) .00342 M

(B) .00752 M

(C) .0132 M

(D) .0294 M

(D) .0294 M

46.3 mL NaOH ⋅ 1 L / 1000 mL ⋅ .287 moles NaOH / 1 L NaOH ⋅ 1 mole HCl / 1 mole NaOH = approx. .015 moles HCl (actual: .0133)

NOTE: You can use the M1V1 = M2V2 equation here, but I prefer to simply use dimensional analysis.

.015 moles HCl / .453 L HCl = approx. .03 M (actual: .0294 M)

Need help with MCAT math? Become an MCAT math wizard using Andrew's High-speed Math Mastery Course @ https://mcatselfprep.com/course/andrews-high-speed-math-mastery-course/

You have a solution of 78.3 mL of HCl. If it takes 56.2 mL of .143 M Ba(OH)2 to reach the end point of our titration of the HCl solution, what is the concentration of HCl in the original solution?

(A) .0205 M

(B) .205 M

(C) 2.05 M

(D) 20.5 M

(B) .205 M

56.2 mL Ba(OH)2 ⋅ 1 L / 1000 mL ⋅ .143 moles Ba(OH)2 / 1 L Ba(OH)2 ⋅ 2 moles OH- / 1 mole Ba(OH)2 ⋅ 1 mole HCl / 1 mole OH- = approx. .015 moles HCl (actual: .01607)

.015 moles HCl / .0783 L HCl = approx. .2 M (actual: .205 M)

Need help with MCAT math? Become an MCAT math wizard using Andrew's High-speed Math Mastery Course @ https://mcatselfprep.com/course/andrews-high-speed-math-mastery-course/

CRB Which of the following terms describes the ability to which a system can resist changes in pH?

(A) Buffering strength

(B) Buffering capacity

(C) Buffering flux

(D) Buffering current

(B) Buffering capacity

Buffering capacity describes the ability to which a system can resist changes in pH.

CRB Within how many pH units of a buffer's pKa is the buffering capacity said to be maintained?

(A) 1 unit

(B) 2.5 units

(C) 0.5 units

(D) This depends on the buffer

(A) 1 unit

Within 1 pH unit of its pKa, a buffer is said to maintain its buffering capacity (have an ability to resist changes in pH).

How do the titration curves of a strong acid and strong base compare to a weak acid and a strong base? Consider buffering capacity, the shapes of the curves, and the equivalence points.

For strong acid, notice the little change in pH until right before the equivalence point, then a sharp increase.

For the weak acid, notice the gradual change in pH as base is added, showing buffering capacity. The middle of that buffering capacity is where pH=pKa. Near its equivalence point, it will also sharply increase.

The equivalence points are halfway between the pH before and after the steep increase.

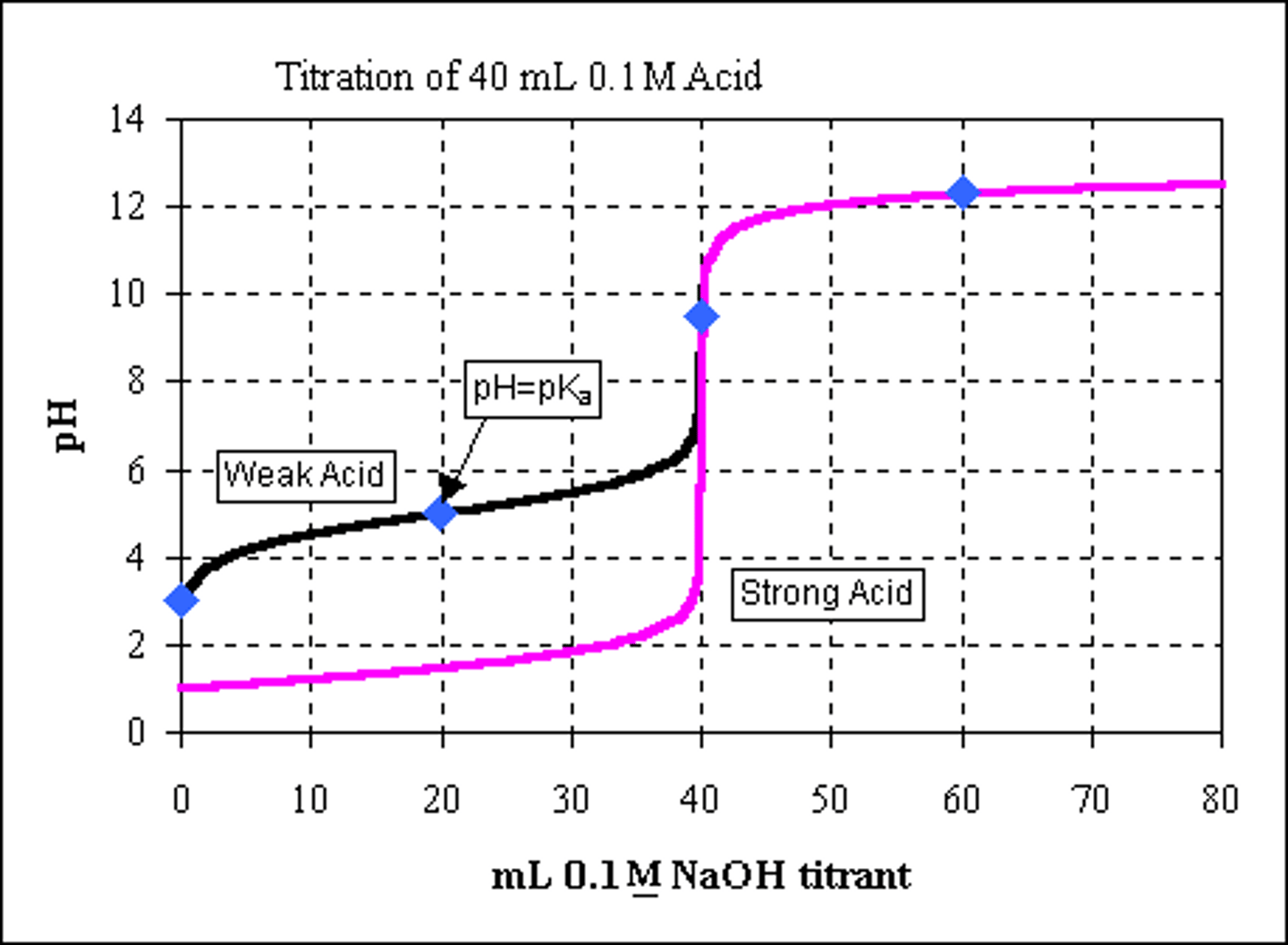
CRB True or false? The equivalence point of a titration using a strong acid and strong base will always be at a pH of 7.

True. The equivalence point of a titration using a strong acid and strong base will always be at a pH of 7.

CRB At which of the following points is the pH equal to the pKa of the titrand?

(A) Equivalence point

(B) Endpoint

(C) Half-equivalence point

(D) Half-endpoint

(C) Half-equivalence point

Recall the Henderson-Hasselbalch equation and the nature of logarithms, especially that log(1)=0.

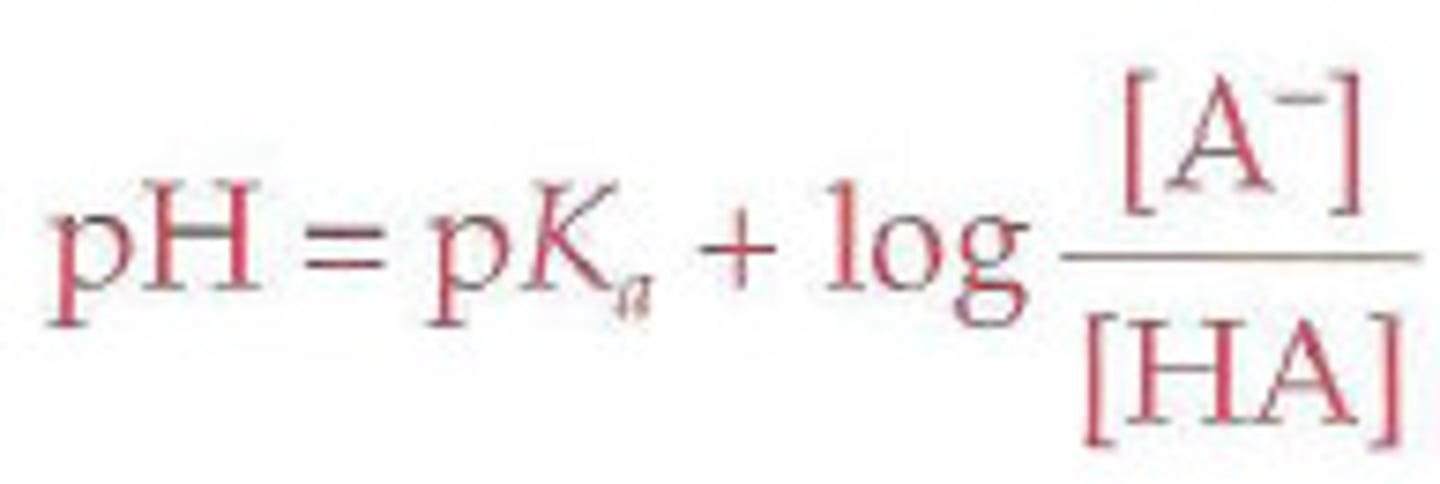
What is the pH of a 4.3 ⋅ 10^-4 M solution of 456.2 mL HCl after having added 23.4 mL of 5.6 ⋅ 10^-5 M NaOH?

(A) .67

(B) 1.43

(C) 2.32

(D) 3.39

(D) 3.39

23.4 mL NaOH ⋅ 1 L NaOH / 1000 mL NaOH ⋅ 5.6 ⋅ 10^-5 mol NaOH / 1 L NaOH = Approx. 10 ⋅ 10^-7 mol NaOH (actual: 13.1 ⋅ 10^-7)

456.2 mL HCl ⋅ 1 L HCl / 1000 mL HCl ⋅ 4.3 ⋅ 10^-4 moles HCl / 1 L HCl = Approx. 2000 ⋅ 10^-7 moles HCl (actual: 1961.66 ⋅ 10^-7)

2000 ⋅ 10^-7 moles HCl - 10 ⋅ 10^-7 mol NaOH = Approx. 1990 ⋅ 10^-7 mol HCl (actual: 1948 ⋅ 10^-7)

1990 ⋅ 10^-7 mol HCl / .4796 L = approx. 4000 ⋅ 10^-7 M (actual: 4062 ⋅ 10^-7)

pH = -log([H+])

pH = -log(4 ⋅ 10^-4)

pH = 3.5 (actual: 3.39)

Need help with MCAT math? Become an MCAT math wizard using Andrew's High-speed Math Mastery Course @ https://mcatselfprep.com/course/andrews-high-speed-math-mastery-course/

What is the pH of a .76 M solution of 173.8 mL acetic acid (Ka = 1.8 ⋅ 10^-5) after the addition of 17.4 mL of .23 M NaOH?

(A) 1.23

(B) 3.42

(C) 5.32

(D) 7.53

(B) 3.42

17.4 mL NaOH ⋅ 1 L NaOH / 1000 mL NaOH ⋅ .23 moles NaOH / 1 L NaOH = approx. 4 ⋅ 10^-3 moles NaOH (actual: 4.002 ⋅ 10^-3)

173.8 mL CH3COOH ⋅ 1 L / 1000 mL ⋅ .76 moles CH3COOH / 1 L CH3COOH =

130 ⋅ 10^-3 moles CH3COOH (actual: 132.088 ⋅ 10^-3)

130 ⋅ 10^-3 moles - 4 ⋅ 10^-3 moles = 126 ⋅ 10^-3 moles CH3COOH

4 ⋅ 10^-3 moles CH3COO-

You can use the HH Equation here if you'd like, but I would just think it through as follows (otherwise it will take you many more steps): "There is more than 10x but less than 100x of the conjugate acid than the conjugate base; therefore, the pH must be between 1 and 2 pH units below the pKa of acetic acid (4.75). My answer must be around 3.

Need help with MCAT math? Become an MCAT math wizard using Andrew's High-speed Math Mastery Course @ https://mcatselfprep.com/course/andrews-high-speed-math-mastery-course/