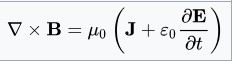EE 330 - Maxwell Equations
Learn
Practice Test
Spaced Repetition
Match
Flashcards1/11
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
12 Terms
The first Maxwell equation states
The electric field diverges from an electric charge, an expression of the Coulomb force
The second Maxwell equation states
There are no isolated magnetic poles, the Coulomb force acts between the poles of a magnet
The third Maxwell equation states
Electric fields (emf) are produced by changing magnetic fields, an expression of Faraday’s law of induction
The fourth Maxwell equation states
Circulating magnetic fields are produced by changing electric fields and by electric currents, Maxwell’s extension of Ampère’s law to include the interaction of changing fields
The integral form of Gauss's Law for Electric Fields
Surface Integral over the Gaussian Boundary, rho is the charge density (total charge per unit volume)
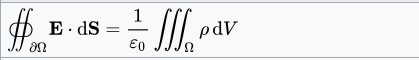
The integral form of Gauss's Law for Magnetic Fields
The integral form of Faraday's Law
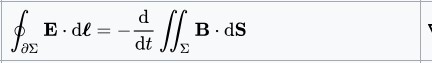
The integral form of Ampere's Law
J is the total electric current density (total current per unit area)
The differential form of Gauss's Law for Electric Fields
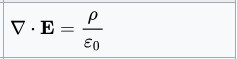
The differential form of Gauss's Law for Magnetic Fields
The differential form of Faraday's Law
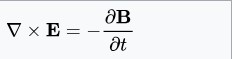
The differential form of Ampere's Law
