Calc 1 Rules and Definitions

Informal Definition of the Limit

lim_x→af(x)=L if we can force f(x) as close as we like to L by choosing x close enough but not equal to a

Formal Definition of the Limit (Epsilon Delta)

For every ε>0, there exists a δ>0 so that if )<lx-cl<δ, then lf(x)l<ε

Squeeze Theorem

If f(x)<g(x)<h(x) and lim_x→∞=L=lim_x→ah(x) then lim_x→ag(x)=L

Intermediate Value Theorem (IVT)

If f is continuous on [a,b] and f(a)<N<f(b), there exists some c in (a,b) were f(c)=N

Limit Definition of the Derivative

f’(x)=lim_h→0[f(x+h)-f(x)]/h

Tangent Line Equation

y-f(a)=f’(a)(x-a)

Mean Value Theorem

If f is continuous on [a,b] and differentiable on (a,b), there exists a c in (a,b) where f’(c)=[f(b)-f(a)]/[b-a]

Rolle’s Theorem

If f is continuous on [a,b], differentialble on (a,b), and f(a)=f(b), then there is a c in (a,b) where f’(c)=0

Fermat Theorem

If f has a local max/min at c, then c is a critical number of f

Extreme Value Theorem

If f is continuous on [a,b], then f attains an absolute max and absolute min on [a,b]

First Derivative Test

If c is a critcal number of f and

1. f’ changes sign from + to - at c, then f has a local max at c

2. f’ changes sign from - to + at c, then f’ has a local min at c

Concavity Definition

f is concave up on an intercal if the graph of f lies above all of its tangent lines on the interval

Second Derivative Test

If f’(c=0 and

1. f”(c)>0, then f has a local min at c

2. f”(c)<0, then f has a local max at c

Newton’s Method

X_n+1=X_n-[f(X_n)]/[f’(X_n)]

Fundamental Theorem of Calculus (FTC) Part 1

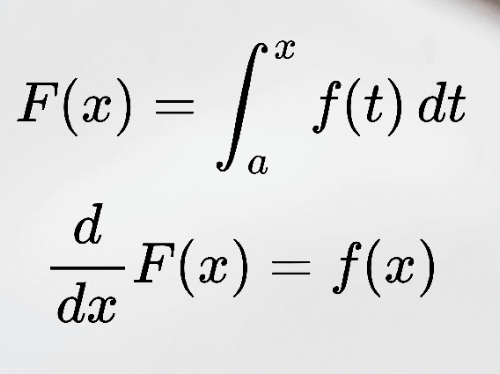
Fundamental Theorem of Calculus (FTC) Part 2

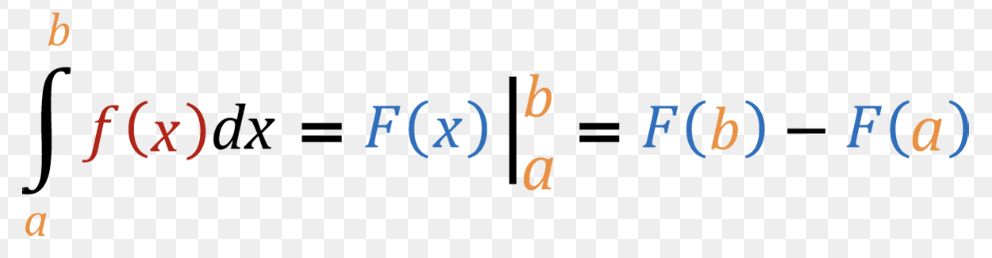
Net Change Theorem

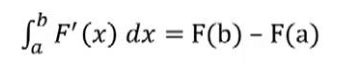
Reimann Sums