Vector Addition

Scalar

A quantity that has a magnitude (value) but does not have a direction

Examples of scalar quantities

Distance, speed, mass, energy, density, power, length, area, volume, time, temperature, work

Vector

A quantity that has both magnitude and direction

Examples of vector quantities

Displacement, velocity, weight, acceleration, force, impulse, momentum, gravity

Arrows

Used to represent vectors

Direction of arrow

Gives the direction of the vector

Length of arrow

Proportional to the magnitude of the vector

2 types of vector addition

Graphical method and Analytical method

Vectors in one dimension

Simple addition and subtraction are all that is needed

2 vectors not along the same line

Simple arithmetic cannot be used in this

2 types of graphical method

Head to tail method and Parallelogram method

Head to tail method/tail to tip method

A graphical way to add vectors. The tail of the vector is the starting point and the head or tip is the final, pointed end of the arrow

Resultant

Vector that starts from the tail of the first vector and ends on the head of the 2nd vector. The sum of the other vectors

Diagonal line drawn from the origin

Parallelogram method

2 vectors are drawn starting from a common origin, and a parallelogram is constructed using these 2 vectors as adjacent sides

Subtracting vectors

Defining the negative of a vector, which has the same magnitude but points in the opposite direction

Arrow pointing left and downward

Negative signed vectors

Arrow pointing right and upwards

Positive signed vectors

Components

Any vector can be expressed as the sum of two other vectors

Trigonometric functions

If the components are perpendicular, they can be found using ____________

X-component of a vector

The projection along the x axis

𝑉𝑥 = 𝑉 cos (angle theta)

Y-component of a vector

The projection along the y axis

𝑉𝑦 = 𝑉 sin (angle theta)

Components

The legs of the right triangle whose hypotenuse is the length of V

Pythagorean theorem

For looking for the resultant

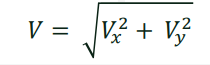
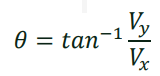
In finding the angle of the resultant vector