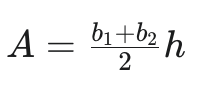Proofs and Theorems
1/94
Earn XP
Description and Tags
2024 Geometry proofs and theorems to know
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
95 Terms
Theorem
a mathmatical statement that can be proved
Must be in Two-Column Proof!
1) Given Info.
2) Focus on the Prove Statement
3) Use and look at the diagram
4) Statements
5) Reasoning
2 Angles Rt. Congruent Theorem
If two angles are right angles, then they are congruent
2 Angles Str. Congruent Theorem
If two angles are straight angles, then they are congruent
Supplementary to Same Congruency
If angles are supplementary to the same angle, then they are congruent
Supplementary to Congruent Angles
If angles are supplementary to congruent angles, then they are congruent
Complementary to Same Congruency
If angles are complementary to the same angle, then they are congruent
Complementary to Congruent Angles
If angles are complementary to congruent angles, then they are congruent
Addition Property (4)
If congruent segments are added to congruent segments, then the sums are congruent
If congruent angles are added to congruent anlges then the sums are congruent
If an angle is added to congruent angles, then the sums are congruent.
If a segment is added to two congruent segments, them the sums are congruent
Subtraction Property (2)
If a segments (or angles) is subtracted from congruent segments (or angles), then the difference are congruent.
If congruent segments (or angles) are subtracted from congruent segments (or angles), then the difference are congruent.
Multiplication Property
If segments (or angles) are congruent, then their like multiples are congruent. (Small to big)
Division Property
If segments (or angles) are congruent, then their like divisions are congruent. (Big to small)
Cue words for Mult. and Div. property
Midpoint, bisects, angle bisector/trisector, etc.
VAT
Vertical Angle Theorem
CPCTC
Corrosponding Parts of Congruent Triangles are Congruent
Radii Congruency
All Radii in a circle are congruent
Median (THINK MIDPT.)
A line (or seg) that extends from the vertex of a triangle to the midpt. of the opp. side
Altitude (THINK PERPENDICULAR)
A line (or seg) that extends from the vertex of a triangle and is perpendicular to the opp. side
Auxiliary Lines Postualte
Two pts. determine a line
Concurrent
Lines that meet at exactly one pt. are conncurrent
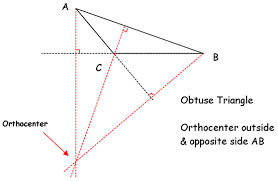
Orthocenter
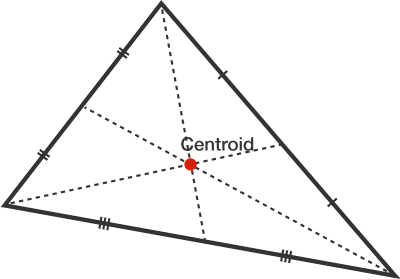
Centroid
ITT
(Isosceles Triangle Thereom) Is a theorem stating that if two sides of a triangle are congruent, then the sides opposite those angles are also congruent.
ITTC
(Isosceles Triangle Theorem Converse) If two angles of a triangle are congruent, then the sides opposite those angles are also congruent.
Triangle Congruency YES
SSS postulate
SAS postulate
ASA postulate
AAS postulate
Triangle Congruency NO
ASS postulate
AAA Postulate
Inverse of ITT
If two sides of a triangle are not congruent, then the angles opposite those sides are also not congruent, and the larger angle opposite the longer side.
Inverse ITTC
If two angles of a triangle are not congruent, then the sides opposite those angles are also congruent and the longer side is opposite the larger angle.
HL Postulate
hypotenuseIf there exists a correspondence between the vertices of two right triangles such that the hypotneuse and a leg of one trinalge are congruent to the corresponding parts fo the other triangle, the two right tringles are congruent
RAT
Right Angle Theorem - If 2 angles are both supplementary and congruent, then they are right anlges
Any pt. on perp. bis Theorem
If a pt. is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of that segment
EDT
Equidistance Theorem - If two points are each equidistant from the endpoints of a segment, the the points determine the perpendicular bisector of the segment.
Perpendicular Bisector Postulate
A Perpendicular Bisector is the shortest path between two points.
Method for Using Indirect Proofs
Either the prove statement is true or false
Assume conclusion is false
Continue w/ proof until you get to a contradiction
State desired conclusion
When you see negations then —>
Indirect Proofs!
Triangle Interior Angle Theorem
The sum of the measures of the angles in a triangle is 180
Remote Interior Angle Equal Theorem
The measure of an exterior angle equals the sum of the measures of the two remote interior angles
Midline Theorem
A segment joining the midpoints of a triangle is parallel to the third side, and its length is one-half the length of the third side.
No Choice-Theorem
If 2 angles of 1 triangle are congruent to 2 angles of a 2nd triangle, then the 3rd angles are congruent
AAS
If there exists a correspondence between the vertices of 2 triangles such that 2 angles and the NON-INCLUDED side of 1 are congruent to the corresponding parts of the other, then the triangles are congruent.
The sum of a polygon's interior angles with n sides is given by the formula.
180(n-2)
The sum of the exterior angles of a polygon, taking one at each vertex, is always ___
360°
The number of diagonals d in an n-sided polygon is given by the formula.
n(n-3) / 2
Each exterior angle E of an equiangular n-sided polygon is given by the formula.
360/n
Individual int angles of regular polygon equation
180(n-2)/n OR 360/n, then answer of that minus 180. Ex. 360/5=72. 180-72=108, aka measure of individual int angles.
MEPT
Means Extremes Product Theorem: a/b = c/d —> a*d = c*b
MERT
Means Extremes Ratio Theorem: a*d = c*b —> a/b = c/d or a/c = b/d (or any of their reciprocals)
Ratio Perimeter 2 Similar Polygons
The ratio of the perimeters of two similar polygons is = to the ratio of any pair of corresponding sides.
AA
Angle Angle - If there exists a correspondence between the vertices of 2 triangles such that two of the angles of one triangle are congruent to the corresponding angles of the other, then the triangles are similar.
SSS~
If there exists a correspondence between the vertices of 2 triangles such that the ratio of the measure of corresponding sides are equal
SAS~
If there exists a correspondence between the vertices of 2 triangles such that the ratio of the measure of corresponding sides are equal, then the triangles are similar.
Side Splitter Theroem
If a line is parallel to 1 side of a triangle and intersects the other two sides, it divides those 2 sides proportionaly. (Look on 8.5 notes for example)
3 parallel lines 2 transversal Theorem
If 3 or more parallel lines are intersected by two transversal, the parallel lines divide the transversals proportionally. (Look on 8.5 notes for example)
(Most imp. Ch. 8 Theorem) Angle Bisector Theorem
If a ray bisects an angle of a triangle, it divides the opposite side into segments that are proportional to the adjacent sides [a/b=d/c OR a/d=b/c] (Look on 8.5 notes for example)
Circumference Equation
2πr or dπ
Area Equation
A = πr 2
If an altitude is drawn to the hypotenuse of a right triangle then:
a. All 3 triangles are similar to each other
b. There exists a mean proportional between 2 other sides of the triangles for each of the 3 sets of triangles (Altitude)
c. Either leg of the given triangle set is the mean proportional between the hypotenuse and the given triangle and the projection of that leg
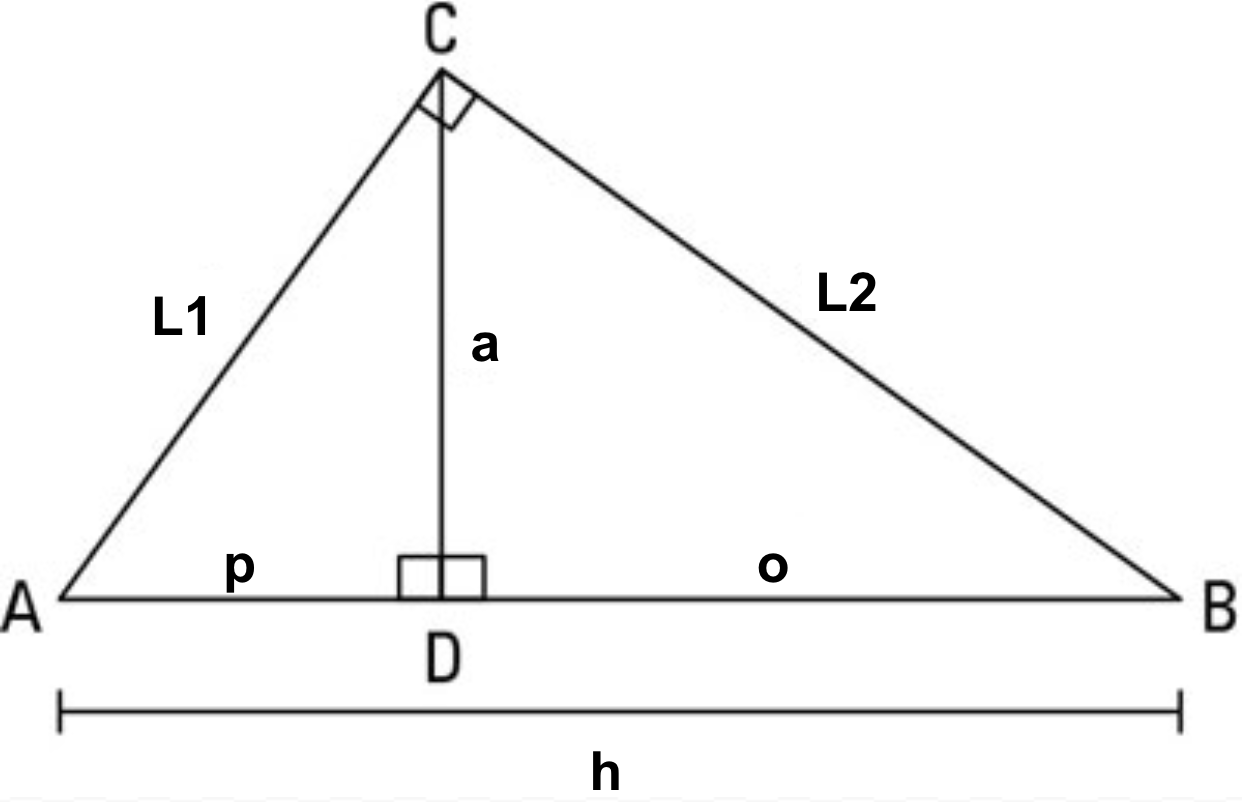
Write the mean proportional (1st one)
Paul Always Ate Oranges:
p/a = a/o
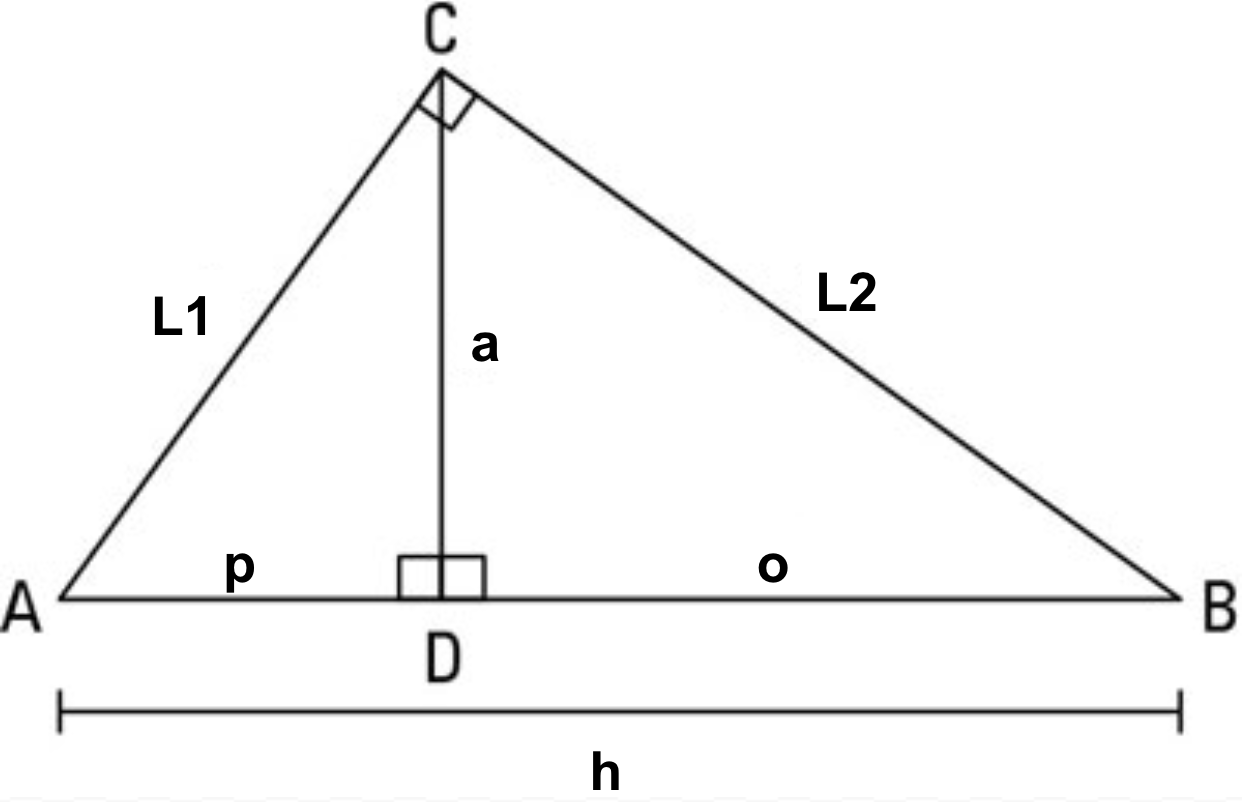
Write the mean proportional (2nd one)
Pretty Little Liars Hate
p/l = l/h
Pythagorean Theorem
a2 + b2 = c2
Converse Pythagorean Theorem
If a2 + b2 = c2 then the triangle is a right triangle
Right:
Acute:
Obtuse:
a2 + b2 = c2
a2 + b2 > c2
a2 + b2 < c2
Common (Ms. Kiesselbach may use) Triples
(3,4,5) (3 root 3, 5 root 3, 4 root 3) (5,12,13) (7,24,25) (8,15,17) (9,40,41)
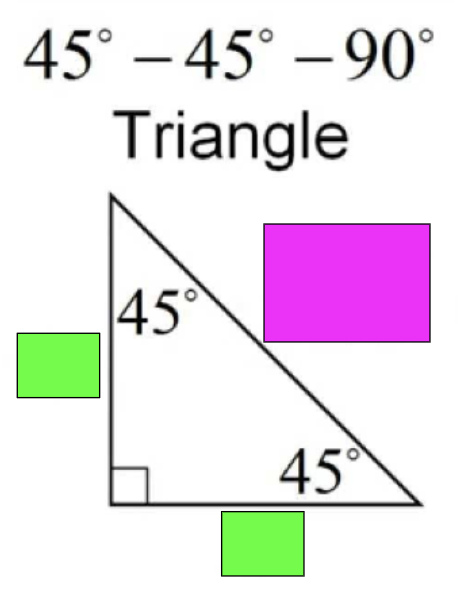
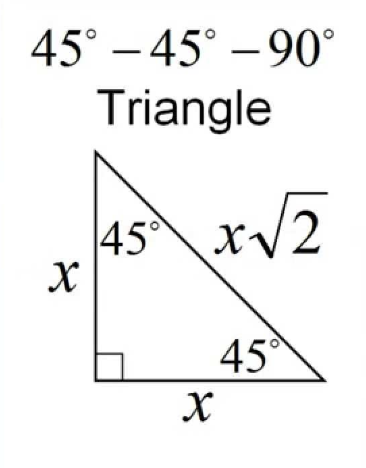
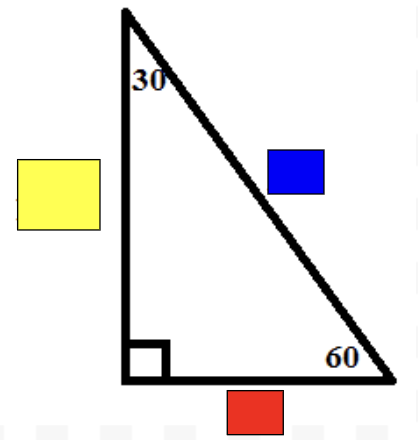
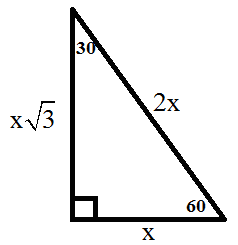
Length Equation
degree of arc/360 (2 pie r)
Measure Equation
degree of arc
Formula for length of the diagonals in a rectangular prism
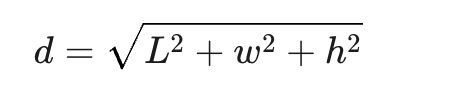
Radius perp. to chord —>
If a radius is perp. to a chord, then it bisects the chord
If radius bis. chord
If radius bis. chord, then it’s perp. to the chord
Perp. bis. of a chord passes…
Perp. bis. of a chord passes through the center of a circle
2 Chords Equidistant Center Circ. then _____
If 2 chords are equidistant from the center of a circle then they are congruent
2 Chords of a circle are congruent then _____
If 2 chords of a circle are congruent then they are equidistant from the center
If arcs of a circle (or congruent circles) are congruent then…
If the arcs of a circle (or congruent circles) are congruent then, their corresponding chords are congruent
If 2 corresponding chords of a circle (or congruent circles) are congruent then…
If corresponding chords of a circle (or congruent circles) are congruent then, their arcs are congruent
If 2 central angles of a circle (or 2 congruent circles) are congruent then…
If 2 central angles of a circle (or 2 congruent circles) are congruent then, their corros. arcs are congruent
If 2 corros. arcs of a circle (or 2 congruent circles) are congruent then…
If 2 corros. arcs of a circle (or 2 congruent circles) are congruent then, their central angles are congruent
If 2 chords in a circle (or 2 congruent circles) are congruent then…
If 2 chords in a circle (or 2 congruent circles) are congruent then, the corros. central angles are congruent
If the corros. central angles in a circle (or 2 congruent circles) are congruent then…
If the corros. central angles in a circle (or 2 congruent circles) are congruent then, the chords are congruent
A tangent line is ____
A tangent line is perpendicular to the radius drawn to the point of contact
If a line is perp. to a radius at its outer endpt. then….
If a line is perp. to a radius at its outer endpt. then it is tangent to the circle
2 Tan. Thm.
2 tangent line segments from same of congruent circles, the tange. segs are congruent
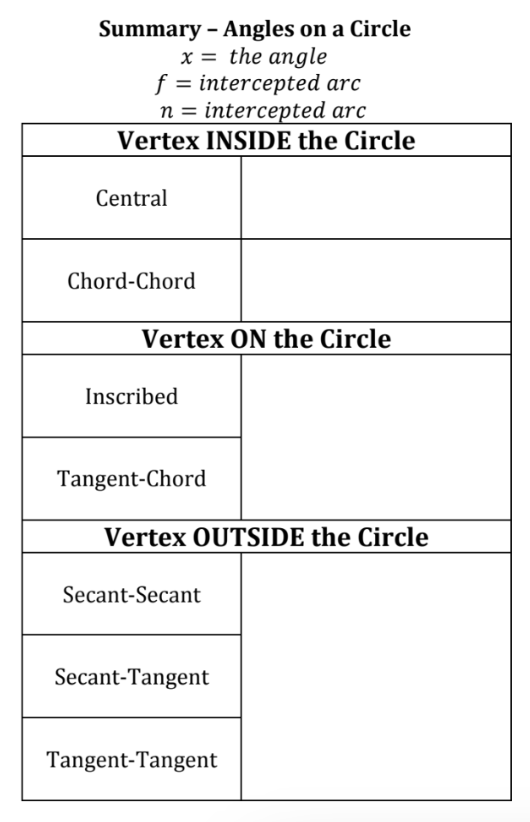
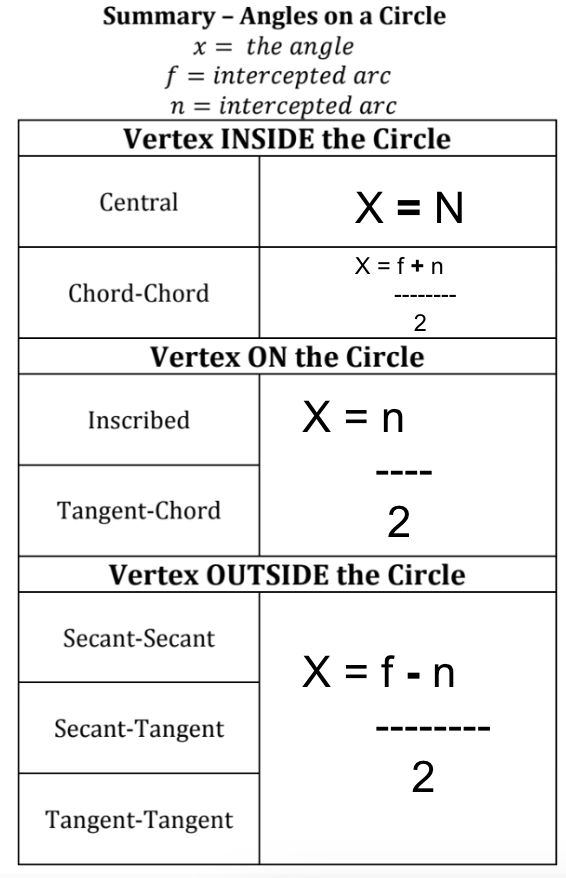
If a quadrilateral is inscribed in a circle, its oppisite angles are ______
supplementary
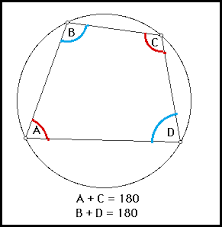
If a parallelogram is inscribed in a circle, it must be a _______
rectangle

If 2 inscribed or chord angles intercept the same or congruent arcs, then they are _____.
congruent
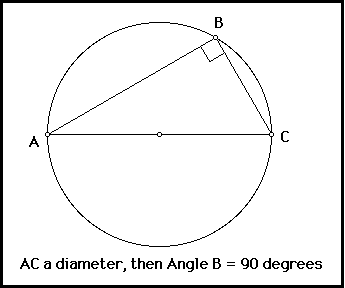
If an angle is inscribed in a semicircle, this it is a _______
right angle
The sum of a tangent-tangent angle and its minor arc is _____
180

Chord-Chord Power Theorem
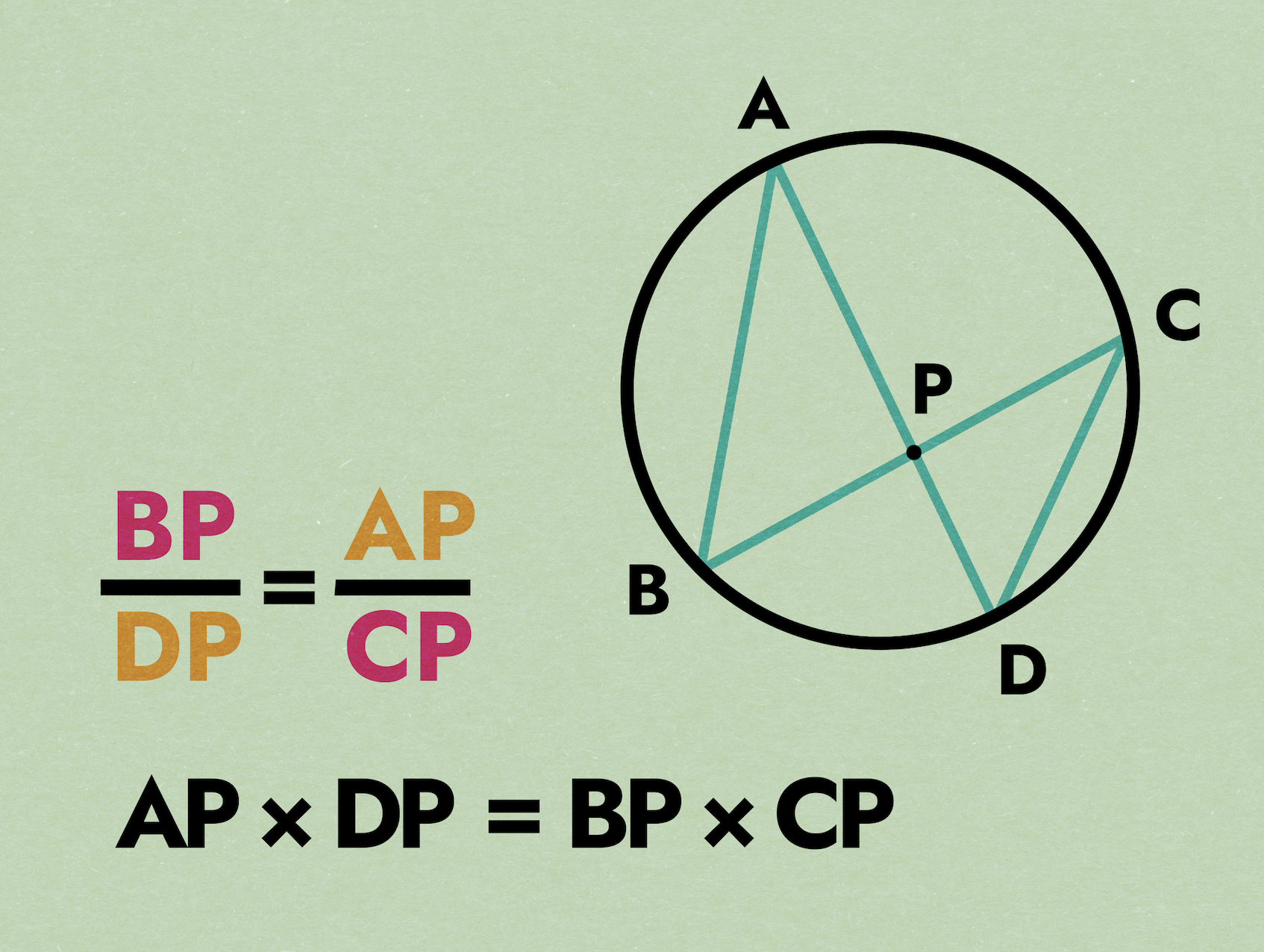
Tangent-Secant Power Theorem
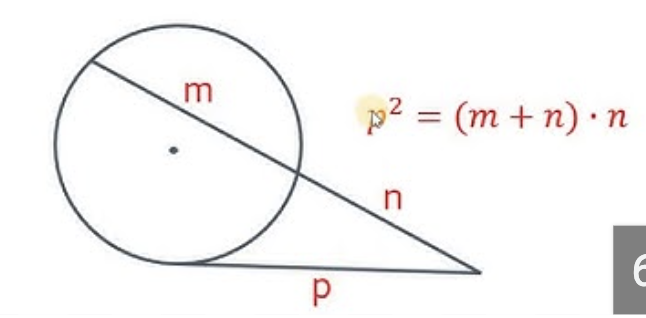
Secant-Secant Power Theorem
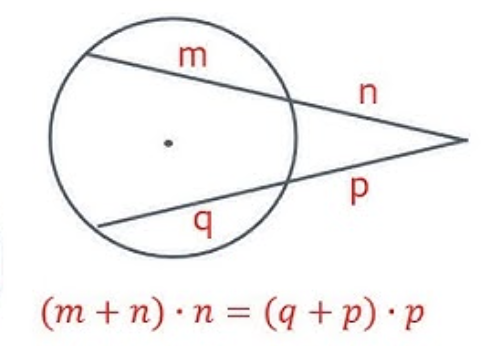
Quadratic Formula
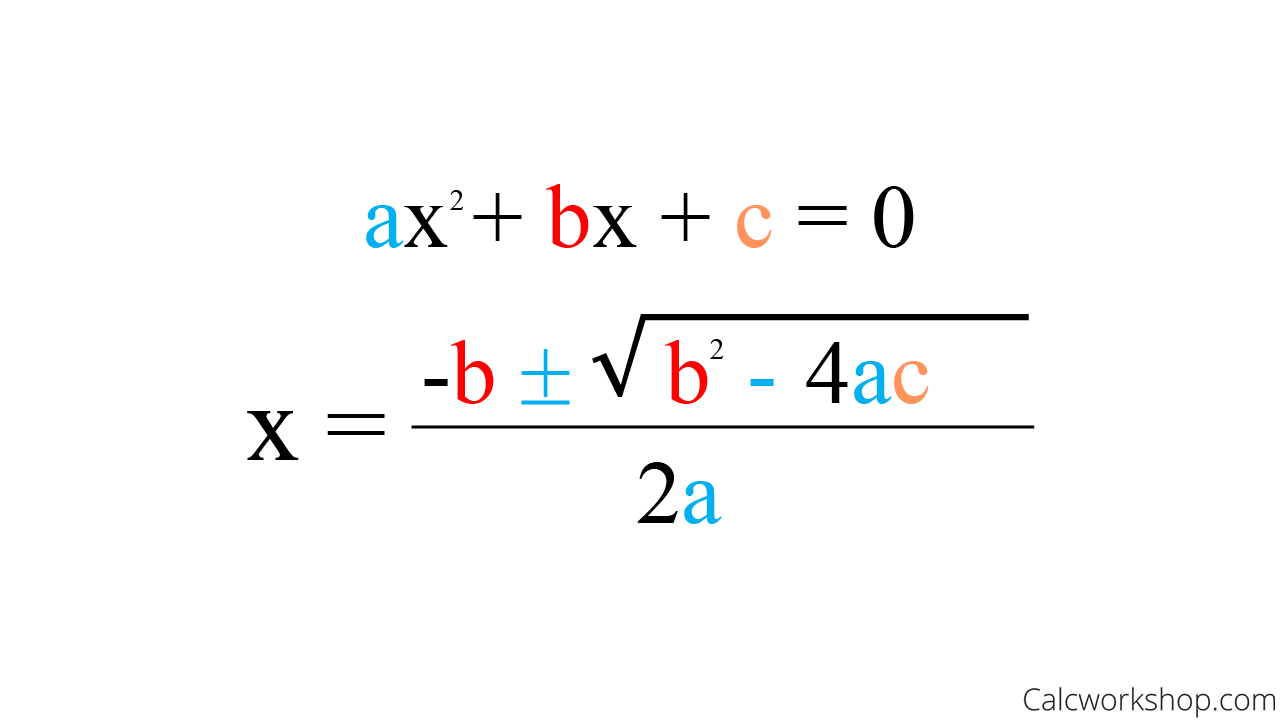
Area of Triangle Equation
A = ½ bh
Parallelogram Equation
A = bh
Trapezoid Equation