Chapter 7: Comparing two means (Dependent Samples)

What is the key difference between independent and dependent samples?

Independent samples: No natural pairing between subjects (Chapter 6).

Dependent samples: Each data point in one sample is linked to a corresponding data point in another sample (e.g., before/after studies).

What is a matched-pairs design?

A matched-pairs design compares two treatments by pairing observations (either the same individual measured twice or two similar individuals).

Why use a matched-pairs design?

It controls for confounding variables by ensuring each subject serves as their own control, reducing variability.

What is the formula for the paired difference (𝑑𝑖)?

How do we analyze paired data statistically?

Convert the data into a single list of paired differences (𝑑𝑖), then apply one-sample t-tests on these differences.

What are the validity conditions for paired t-tests?

1. 𝑛𝑑 ≥ 30 → Central Limit Theorem applies

2. 𝑛𝑑 < 30 but data is normal/symmetric → t-test is valid

3. 𝑛𝑑 ≥ 20 and not strongly skewed → Robust condition

What are the hypotheses for a paired t-test?

• Null hypothesis (H₀): \mu_d = 0 (No difference between paired observations)

• Alternative hypothesis (Hₐ): \mu_d \neq 0, \mu_d > 0, or \mu_d < 0

 What is the test statistic for a paired t-test?

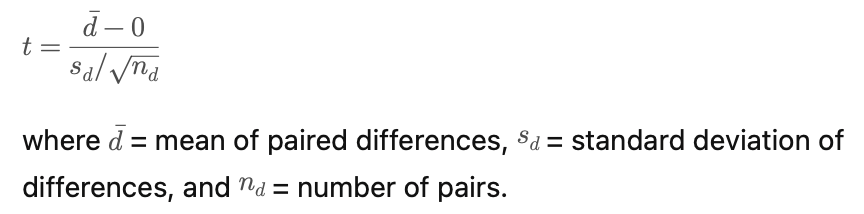
How do you interpret p-values in a paired t-test?

• p < α (0.05) → Reject H₀ → Significant difference

• p > α (0.05) → Fail to reject H₀ → No significant difference

What is the formula for a confidence interval in paired t-tests?

Why use simulation for paired samples?

If normality assumptions are not met, we use randomization methods to create a null distribution for hypothesis testing.

How does the randomization method work for matched pairs?

1. Keep pairs together

2. Randomly flip the sign of each difference (i.e., swap before/after labels)

3. Calculate new mean differences and compare with the observed statistic

 What are the key steps for a paired simulation hypothesis test?

1. Compute paired differences (𝑑𝑖)

2. Simulate null distribution (randomization)

3. Compute observed mean difference

4. Compare with simulated distribution → Find p-value

How do you construct a 95% confidence interval using the 2SD method?

Why does pairing matter?

If we ignore pairing and use an independent t-test instead, we risk:

• Increased variability

• Masking real effects

• Wrong conclusions

What happens if we mistakenly treat dependent samples as independent?

The independent t-test loses power, and we might fail to detect a significant effect.

What is the Wilcoxon Signed-Rank Test?

A: A non-parametric alternative to the paired t-test that tests whether the median difference is 0.