Limits, Infinite Limits, Continuity

How do you know if a function is continuous at a number “a”? What does it mean?

lim x→a f(x) = f(a)

it means that:

1. a is in the domain of f

2. lim x→a f(x) exists

3. lim x→a f(x) = f(a), its one sided limits also need to equal f(a)

What do you say if a function is not continuous at a number “a”

The function is discontinuous, or f has a discontinuity at a

What is the definition for one-sided continuity?

lim x→ a⁺ f(x) = f(a)

• f is continuous from the right of a
  or

lim x→a⁻ f(x) = f(a)

• f is continuous from the left of a

(In words/broadly/main idea, not mathematically) How do you know if a function f is continuous on an interval?

f is continuous on an interval if:

• f is continuous at every single x-value in the interval

Intuitively, what is a continuous function?

A function where you don’t have to lift your pencil to follow it (it doesn’t “break” or have “pieces”, it’s all one connected line)

When you are given a graph, and it asks you to identify and classify points of discontinuity, how do you do it? And how do you explain the function?

CHECK FOR EVERY X-VALUE:

Use the definition lim x→a f(x) = f(a)

• continuous - definition works

• discontinuous - definition does not work

You list your points of discontinuity as “x=(the x-value that is discontinuous)”

How do you know if the following functions are continuous?

1. f ± g

2. cf (c is a constant)

3. fg

4. f/g

NOTE - For these to be true: f and g must be continuous at a

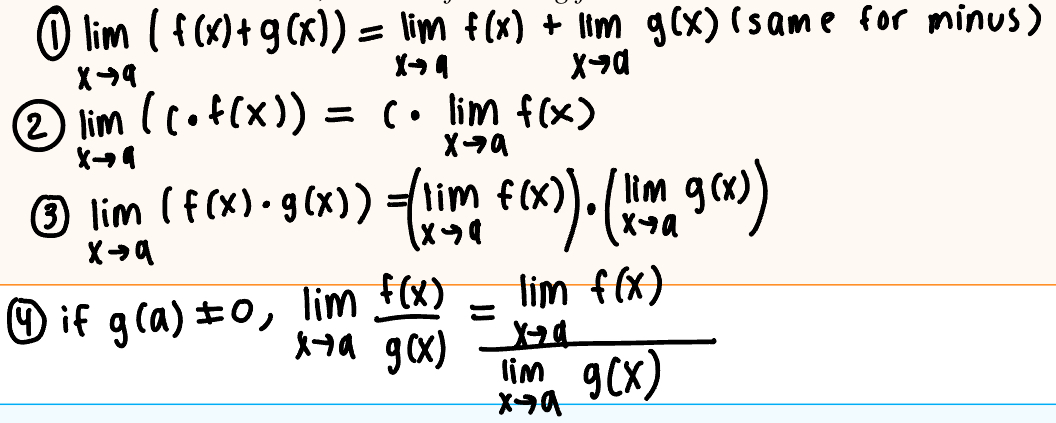
Which functions are continuous at every number in their domains?

• polynomials

• rational functions

• algebraic functions

• trigonometric functions

• exponential functions

• logarithmic functions

Domain of logs? Alone and in fractions?

Alone: >0

On numerator: >0 and combine with domain of the denominator

On denominator: >0 and can’t equal to 0

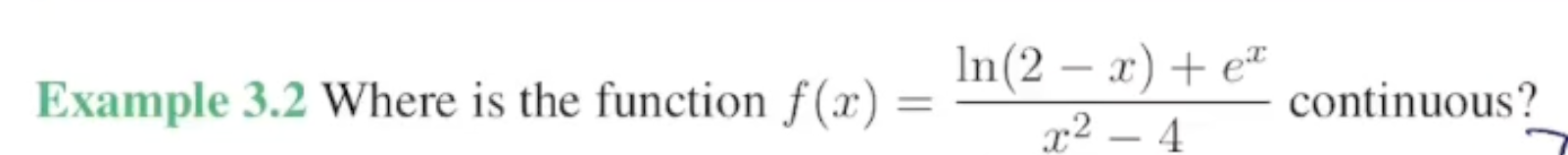
Practice

answer

How do you find the value of k so that the function is continuous on all real numbers? (explain the steps + do the practice problem)

answer

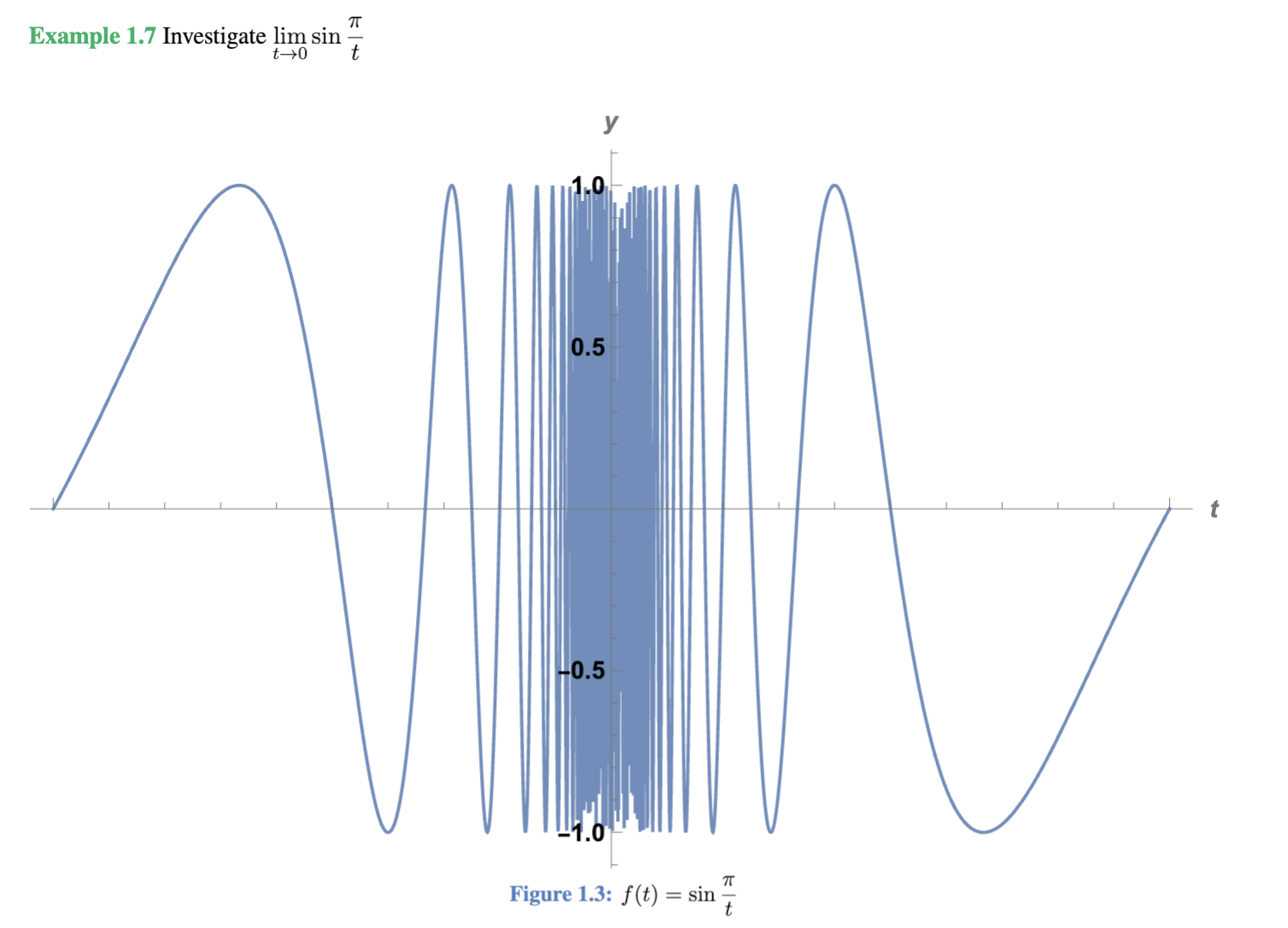
Practice problem, and explain your answer

DNE because the function oscillates infinitely many times as t → 0

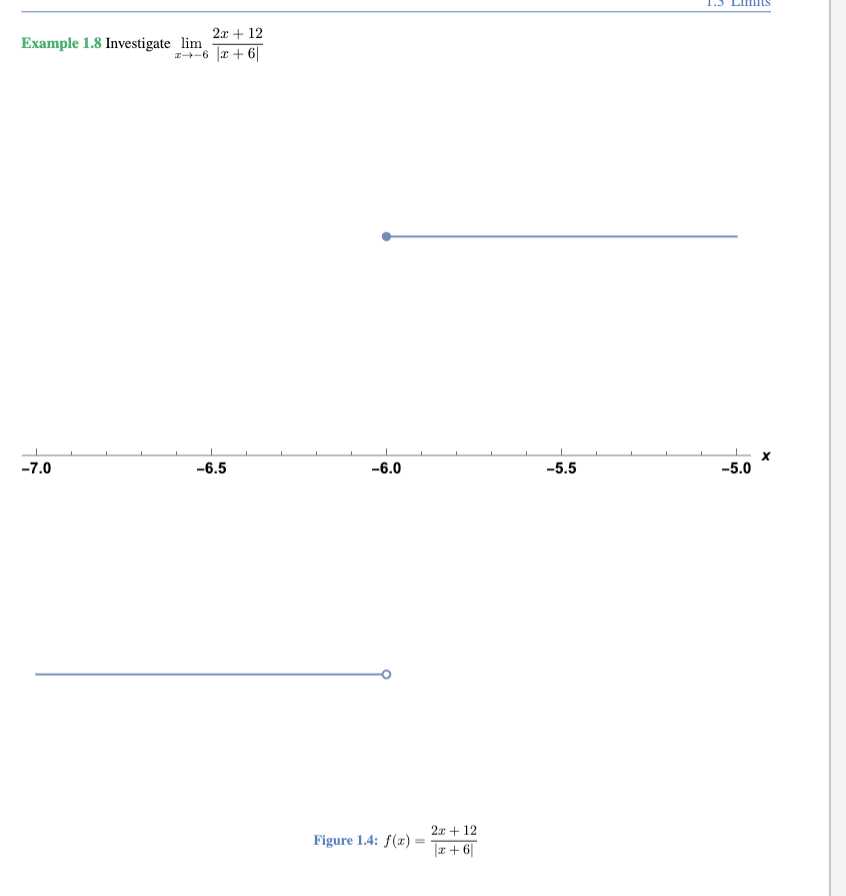
Practice problem

DNE because there is a hole and a point x= -6

n/a

n/a

How do you know that the line x=a is a vertical asymptote/what are the definitons?

If any of the following are true

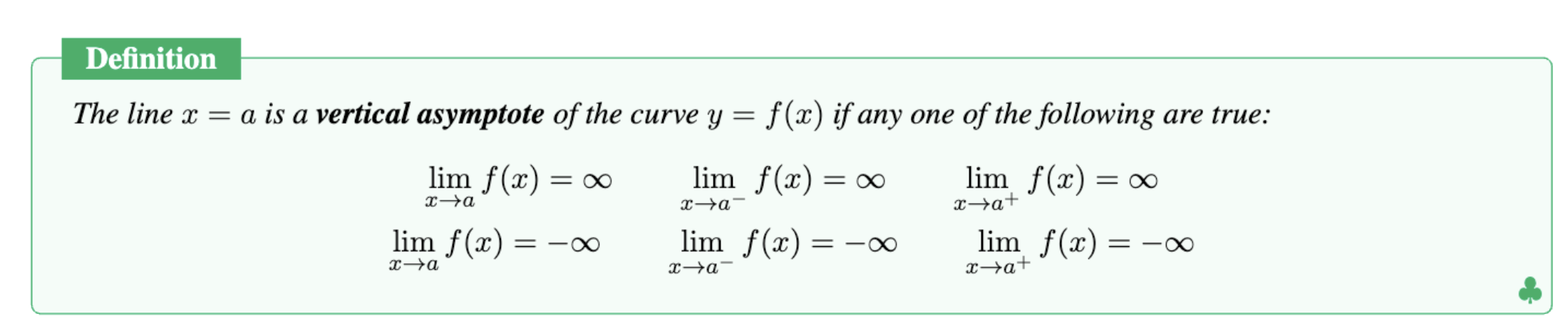
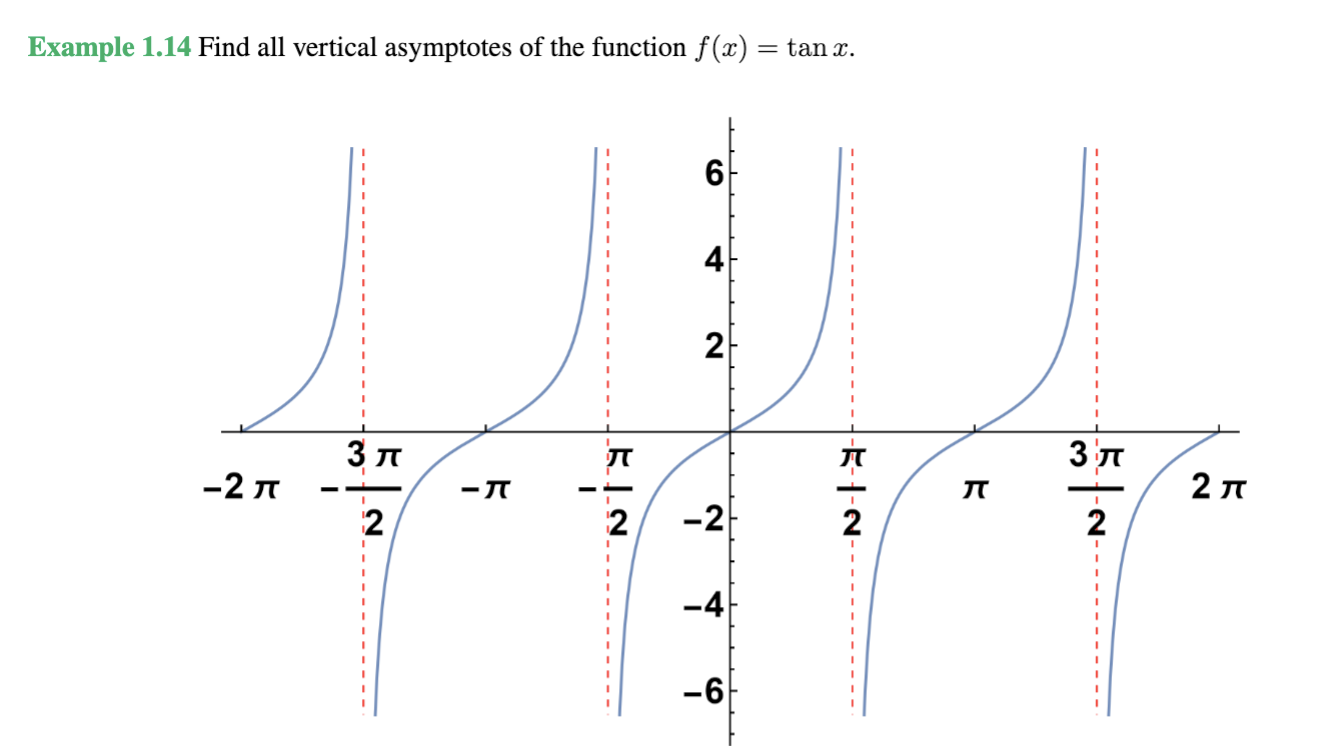
Practice problem

x=-3pi/2, -pi/2, pi/2, 3pi/2

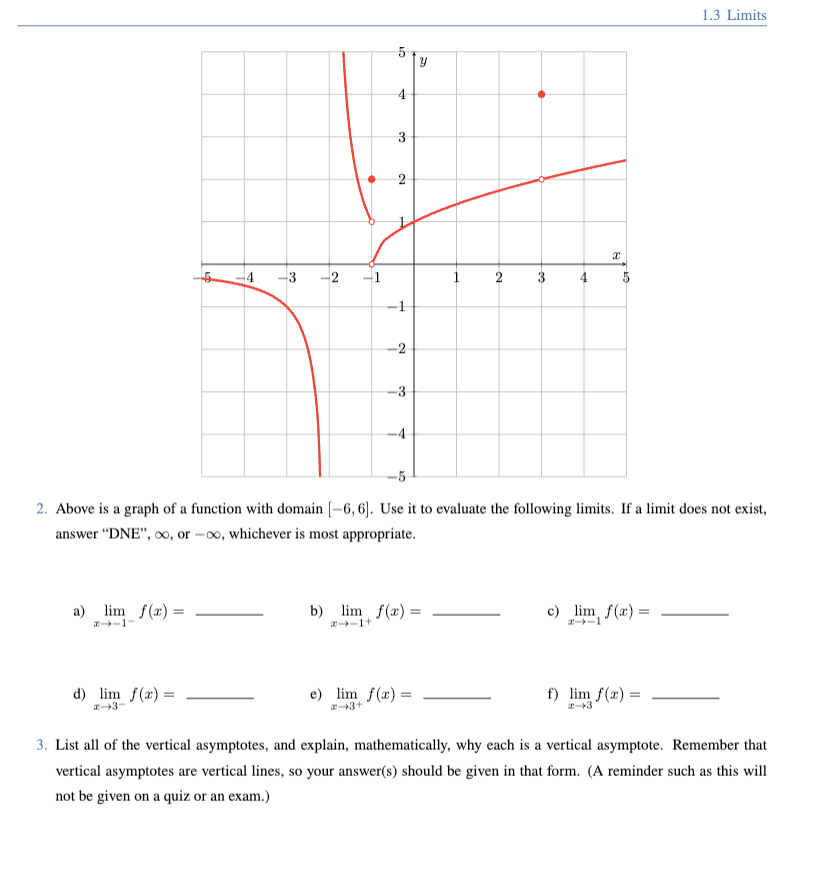
Practice problem (only problem 3)

Answer (use the definitions of vertical asymptotes)

How do you solve a limit with just a polynomial?

Plug a inside the function

How do you solve a limit that is a fraction with simplified polynomials?

ex) lim x→ -3^+ x+2/x+3

1. Plug in the x

2. If you get 1/0, (or a nonzero number divided by 0), solve for an infinite limit

3. In this example, you plug in a number VERY VERY close to -3, but just to the right of it because the limit is coming from the right (ex. plug in -2.99 into the equation)

4. When you plug in the number into the equation, just focus on what sign the num/den is, and divide those signs together. then, write infinity with the sign, and that is your answer

Explain these limit laws and the condition they need to exist:

1. Sum/difference law

2. Constant

3. Product law

4. Quotient law

5. Power law

6. Root law

How do you solve a limit if you plug a point in and get 0/0 as a result?

Expand your equations and try again

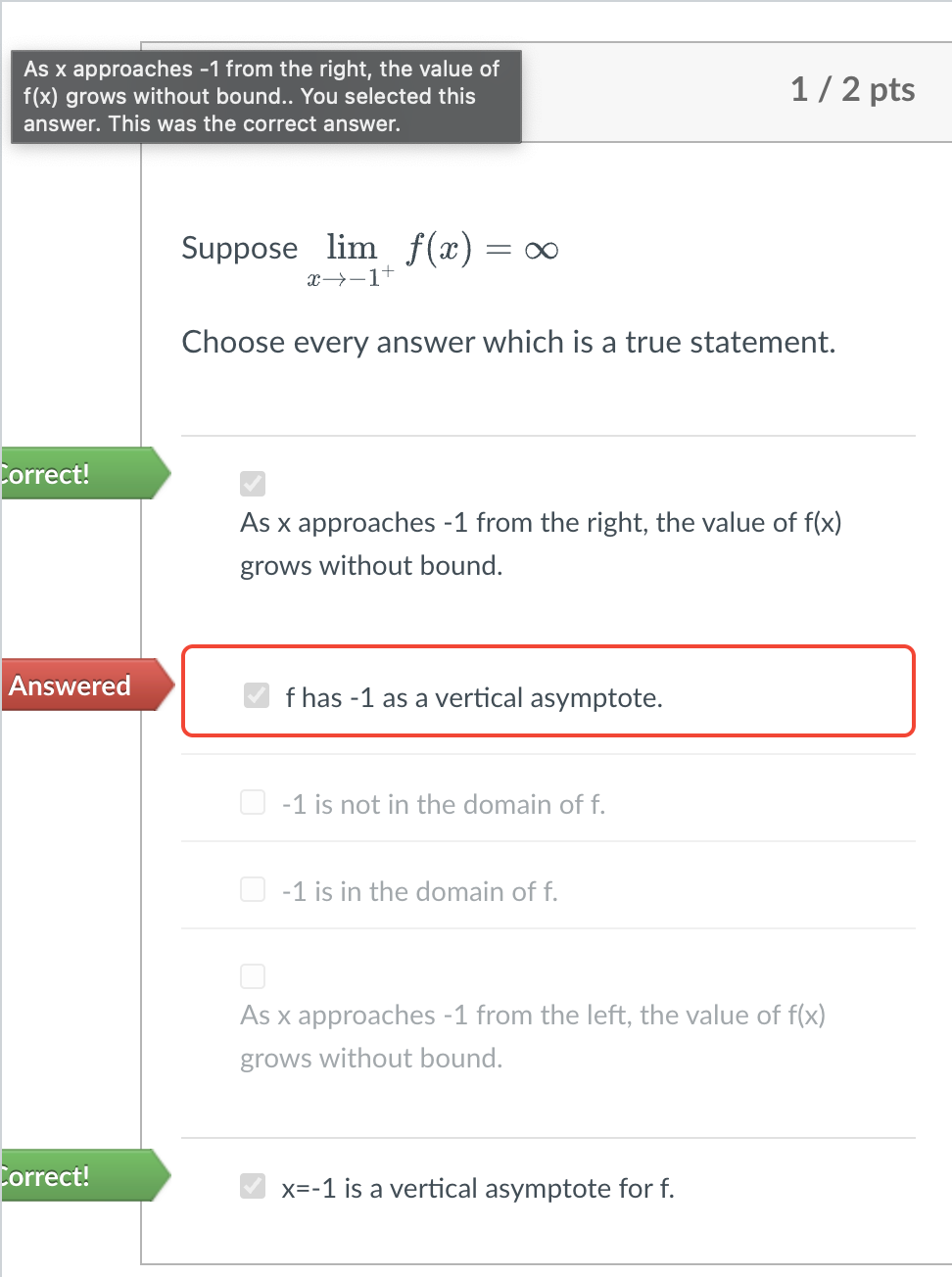
Why was that answer wrong?

Because vertical asymptotes are ALWAYS written in the form “x=#"

Explain the direct substitution property

If a function is one of the following types:

1. Polynomial function

2. rational function

3. algebraic function

Then:

if the function is defined at x=a, then lim x→a f(x) = f(a)

Let’s say there are two functions. The functions never meet except at one point where x=a, where one function has a hole, and the other has an actual solution. Can their limits equal each other at x=a, and if so how do you explain it?

If lim x→a g(x) exists, then lim x→a f(x) = lim x→a g(x)

(basically, one limit has to actually exist at x=a for this to be true)

Explain what the squeeze theorem is

If:

1. h(x) ≤ f(x) ≤ g(x)

2. lim x→a f(x) = L = lim x→a h(x) = L

Then:

lim x→a g(x) = L

Assuming:

8-x³≤f(x)≤8+x³, what is lim x→0 f(x)?

By squeeze theorem,

h(x)≤f(x)≤g(x),

and lim x→0 h(x) = L = lim x→0 g(x) = L, then

lim x→0 f(x) would mean you insert 0 into one of the functions, so

8-(0)³ = 8, so

lim x→0 f(x) = 8

What is the IVT?

if:

1. f is a continuous function on [a,b]

2. N is a number between f(a) and f(b)

3. f(a) does not equal f(b)

then:

• an x-value, “c”, exists in (a,b) such that f(c )=N

Show that there is a solution to the equation

x^4+x-3=0 in the interval (1,2)

Practice problem where you apply the IVT

1. Define your function

   • ex) let f(x)=x^4+x-3

2. Explain how your function is continuous on all real numbers

   • ex) polynomials are continuous on all real numbers on their domain, f(x) is continuous on (1,2)

3. Plug in the end points of the given interval into the function

   • ex)

     • f(1) = -1

     • f(2) = 15

4. Use this answer template:

   1. “since f(one number you plugged in from the end point of the interval) >0, and f(another number you plugged in from the end point of the interval) <0, and f(x) is continuous on (given interval), by the IVT there must be a c in (given interval) so that f(c )=0”

      • ex) Since f(1) < 0 and f(2) >0, and f(x) is continuous on (1,2), by the IVT there must be a c in (1,2) so that f(c )=0

What is the theorem for finding the limit of a composite function?

If:

1. lim x→a g(x)=b

2. f is continuous at b

Then:

• lim x→a f(g(x)) = f(b)

• or

• lim x→a f(g(x)) = f(lim x→a g(x))

How do you know when a composite function is continuous?

If:

1. g is continuous at a

2. f is continuous at g(a)

Then:

• f(g(x)) is continuous at a

• OR

• lim x→a f(g(x)) = f(g(a))