Chapter 14 - Oscillations

Periodic Motion

If an object oscillates back and forth over the same path, each cycle taking the same amount time

Mass spring system assumptions

• surface is frictionless

• mass of the spring is negligible

Equilibrium position and how displacement is measured

Equilibrium position is where the forces are balanced and there is no acceleration; when the sum of forces are equal to zero .

Displacement is measured wrt to the equilibrium position.

Condition for Harmonic Motion

The restoring force F exerted is proportional to the displacement x

Comments/Notes regarding the mass spring system

• The force is not constant, thus, the acceleration is not constant either

• Hooke’s law is only valid in the elastic region of the spring and thus the spring mass system is only considered harmonic/periodic in this region as well

Displacement (x)

measured in meters wrt to the x_eq

Amplitude (A)

is the maximum displacement (pos or negative)

A Cycle

A full back and forth motion of the oscillation

Period (T)

Measured in seconds. The time required to complete a cycle

Frequency (f)

measured in Hz. Th e number of cycles completed per second

f = 1/T

Vertical Mas Spring System

The same as a normal mass spring system but the location of the x_eq is a little different

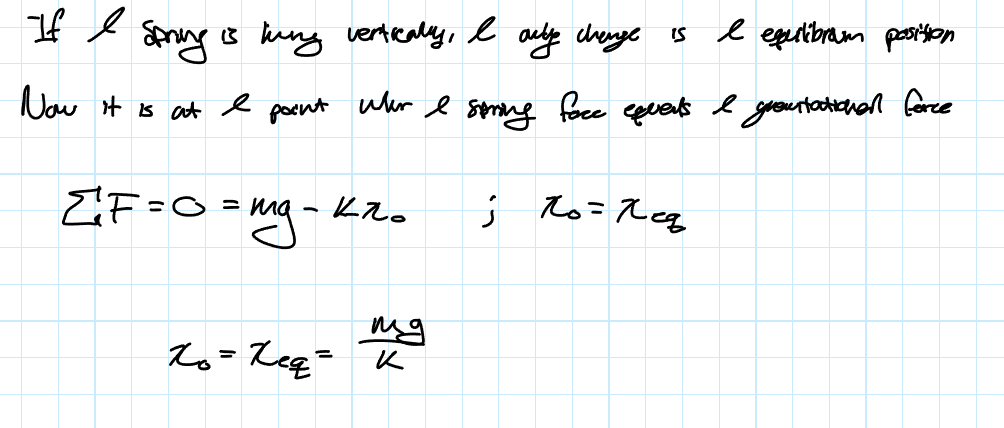
Simple harmonic motion

any system where the restoring force is proportional to the negative displacement is in SHM and is normally called a simple harmonic oscillator (SHO)

Deriving the general solution for the displacement of a SHO

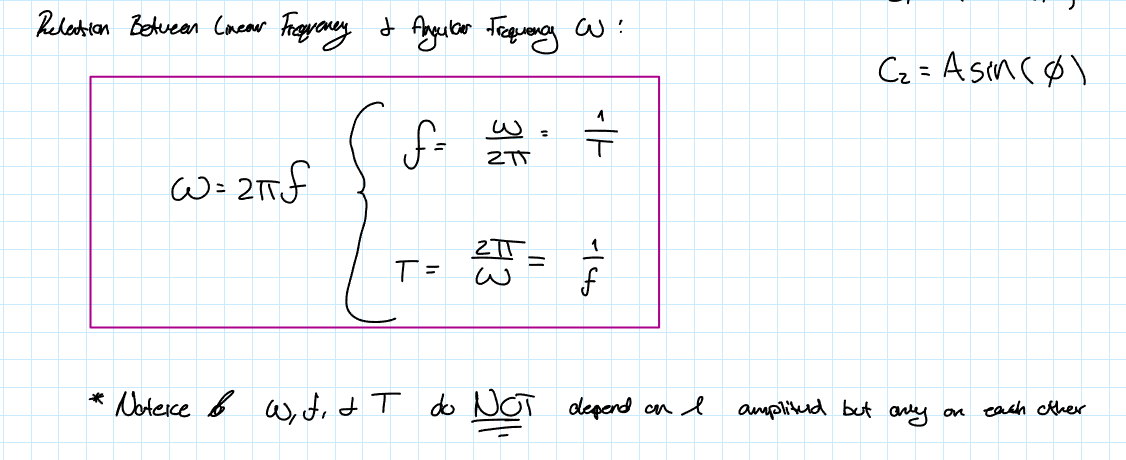
Relation between linear frequency and angular frequency (ω)

angular frequency, linear frequency, and period do NOT depend on amplitude. They only depend on each other.

Kinematics of SHO

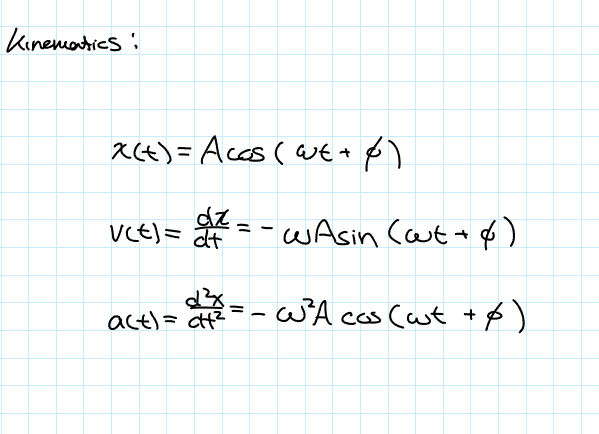
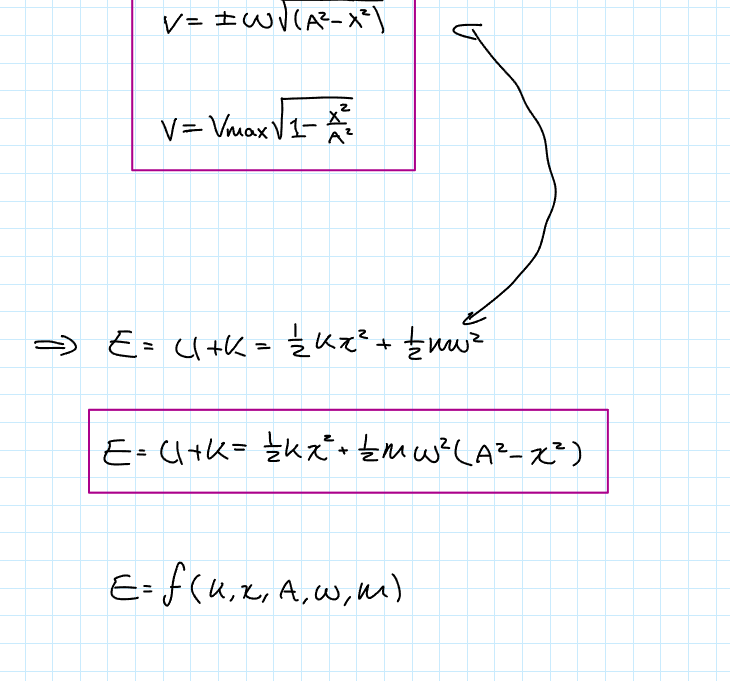
Energy in the SHO

The total mechanical energy will be conserved since we made the assumption that the system is frictionless → Only conservative forces

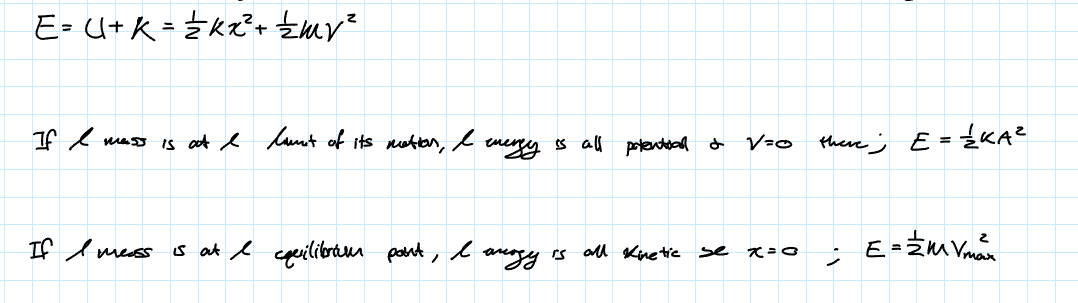
Expression for Maximum velocity

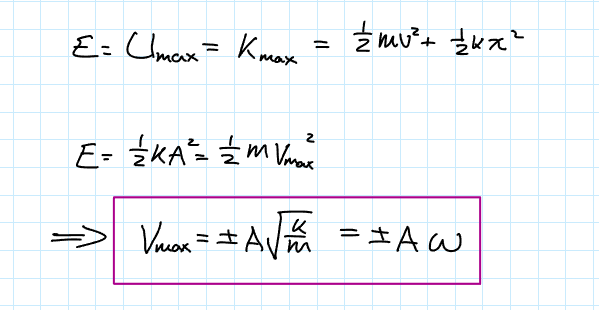
Expression for Velocity

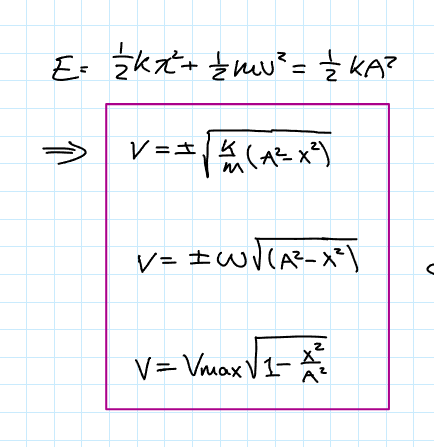
Energy as a function of the spring constant, displacement, amplitude, angular frequency, and mass

SHM Related to Uniform Circular motion

Consider an object moving in a cricle of radius A at a constant speed v_max. If we project its velocity onto the x-axis it follows…

Simple Pendulum Description and Assumptions

A SP consists of a mass at the end of light weight chord.

• Chord does not stretch

• the mass of the chord is negligible

m=mass

L=length of pendulum

θ=the angle the chord makes wrt the vertical equilibrium position (radians)

g=gravitational acceleration

F_T=tension force of the chord (N)

Does the Pendulum Satisfy the requirements of SHM by deffult?

No. For SHM the restoring force must be proportional to the negative displacement. This is not satisfied in any pendulum by defult but with some assumptions this can be satisfied.

Simple Pendulum Displacement Solution

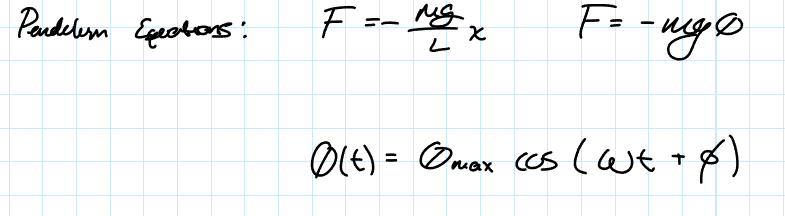
Simple Pendulum Angular Frequency and Linear Frequency

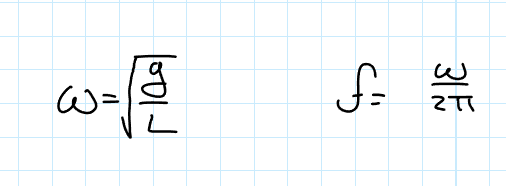
Simple Pendulum Period

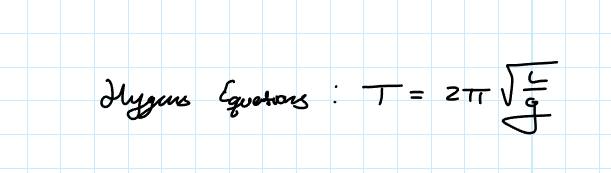
Approximating the acceleration due to gravity with a simple pendulum

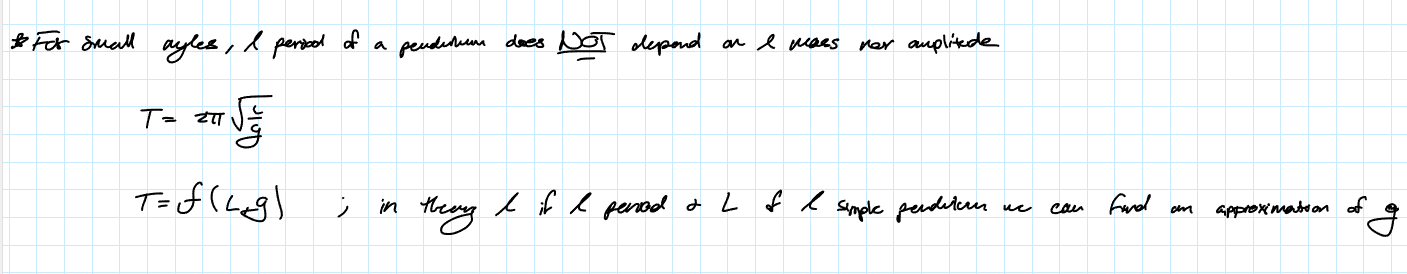
Simple Pendulum Energy Equation

For a simple pendulum mechanical energy is also conserved

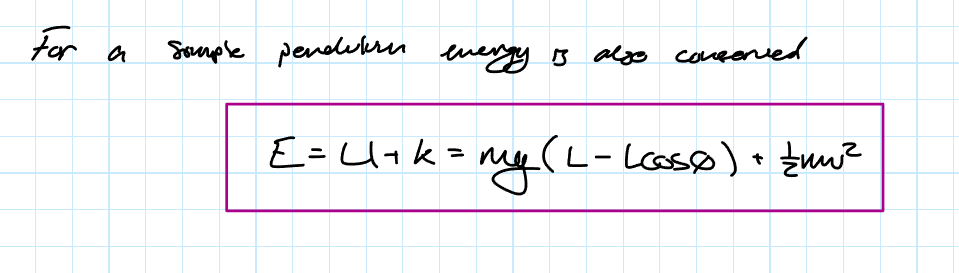
Physical Pendulum Description

A PP is any real extended object that oscillated back and forth.

O=the rotation point

CG=the center of gravity of the pendulum

m=mass

h=the distance between the CG and O

θ=the angle the PP makes wrt the vertical equilibrium position (rad)

EOM of the Physical Pendulum

Only for small angles of theta

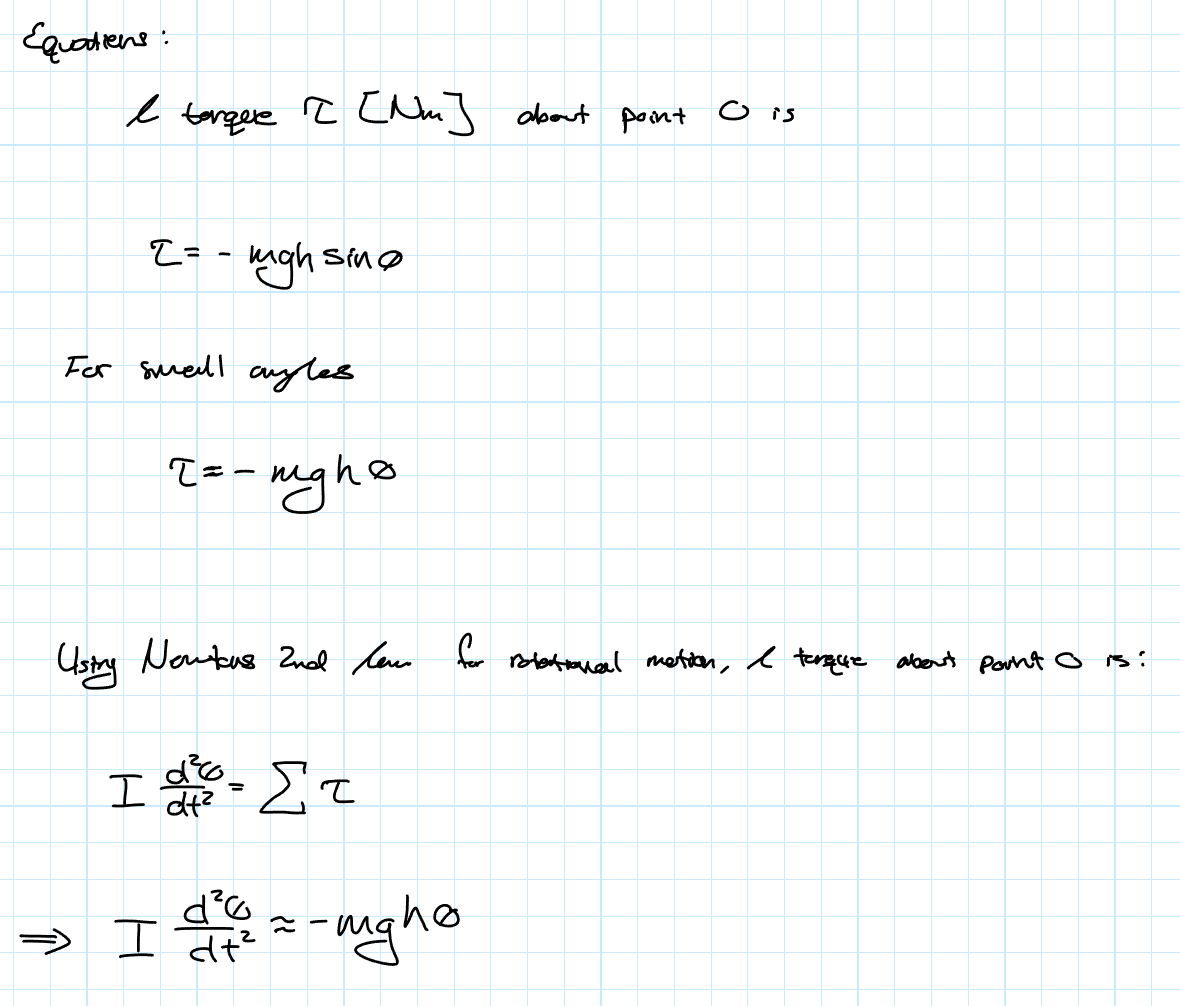
Physical Pendulum Displacement Solution

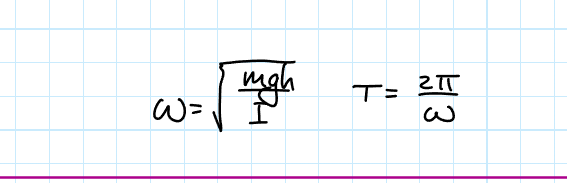
Physical Pendulum Angular Frequency and Linear Frequency

Torsion Pendulum

A TP is one that twists rather than swings. The motion is SHM as long as the wire obeys Hooke’s Law.

k=constant that depends on the wire

I=the moment of inertia of the disk

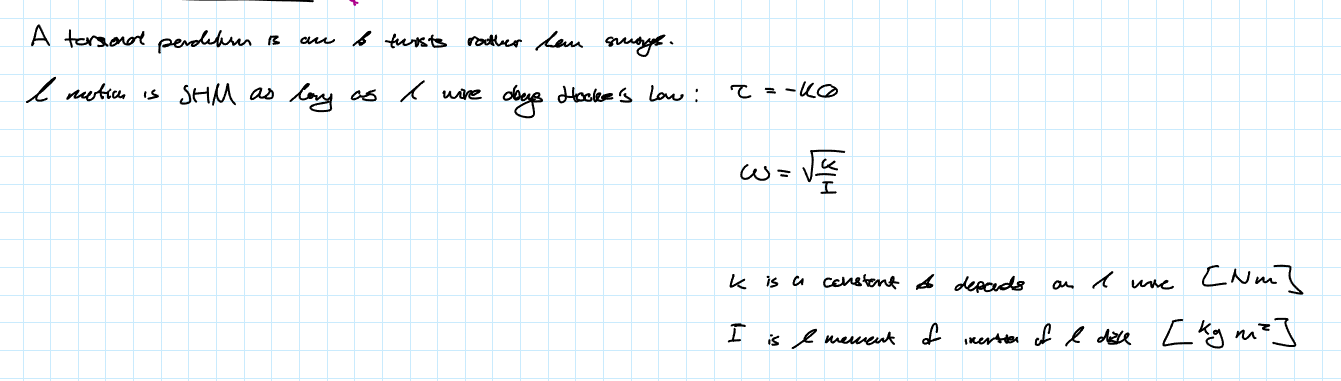
Damped Harmonic Motion

In a more realistic scenario, damped harmonic motion includes a friction or drag force that gradually attenuates the oscillation. we can represent this with a velocity dependent damping term that depends on a damping constant b, measured in [kg/s]

Solving the Damped Harmonic Oscillator

The damping can be treated as an envelop that modifies the undamped oscillation of the SHM.

The damping constant ‘b’ influences this envelop, as well as the (damped) oscillation frequency ‘ω

Gamma Constant in the Damped Harmonic Oscillator

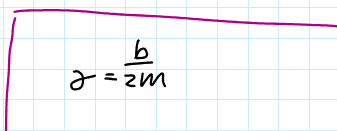
New Frequency in a Damped Harmonic Oscillator (Mass sprig example)

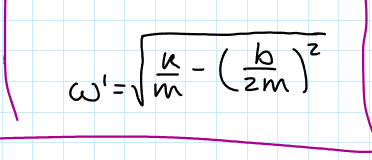
(Types of Damped Harmonic Motion) Underdamped

When b²<4mk or ω’²>0

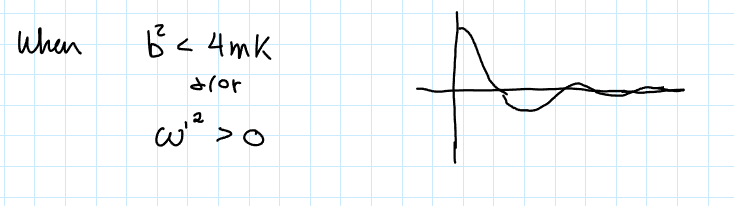
(Types of Damped Harmonic Motion) Critically Damped

when b²=4mk or ω’²=0.

This results in the case in which the system reaches equilibrium in the shortest time, compared to the other dampening cases)

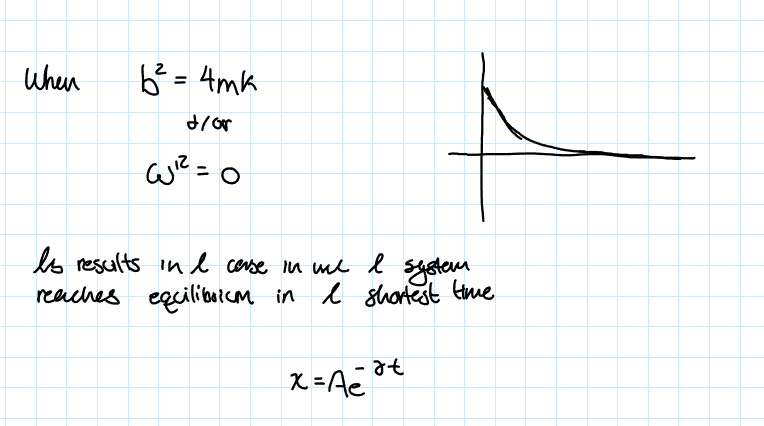
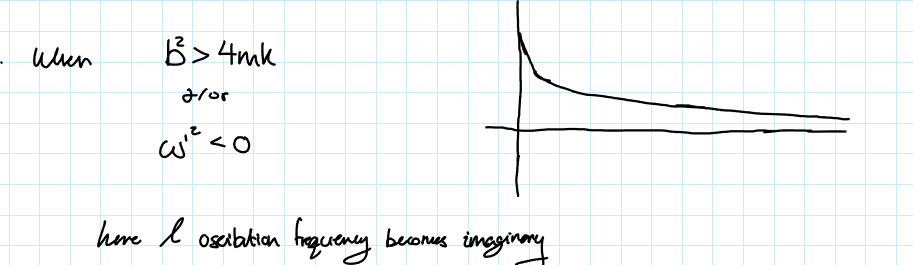
(Types of Damped Harmonic Motion) Overdamped

When b²>4mk or ω’²<0.

Here the oscillation frequency becomes imaginary (the displacement solution has imaginary components)

Forced Oscillations

A FO occurs when there is a periodic driving force affecting the SHO

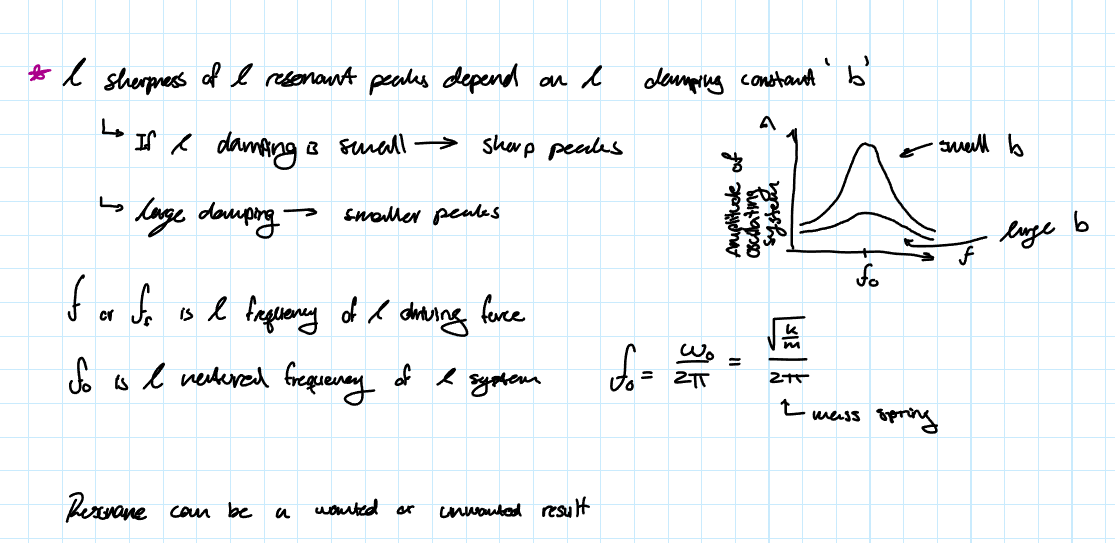
When does Resonance Occur

The frequency ω_f or ω of this driving force might be tyhe same as the natural frequency of the system (ω₀=\sqrt(k/m) for the mass spring system). Resonance occurs when ω_f=ω₀, which causes the oscillation amplitude to become very large

About the Sharpness of the Resonant Peaks

The sharpness depends on the damping constant ‘b’.

If the damping is small →Sharp peaks

Large damping →Smaller peaks

For resonance to be considered, it is usually assumed a damped SHO

Damped and Driving Force Harmonic Oscillator Displacement Solution

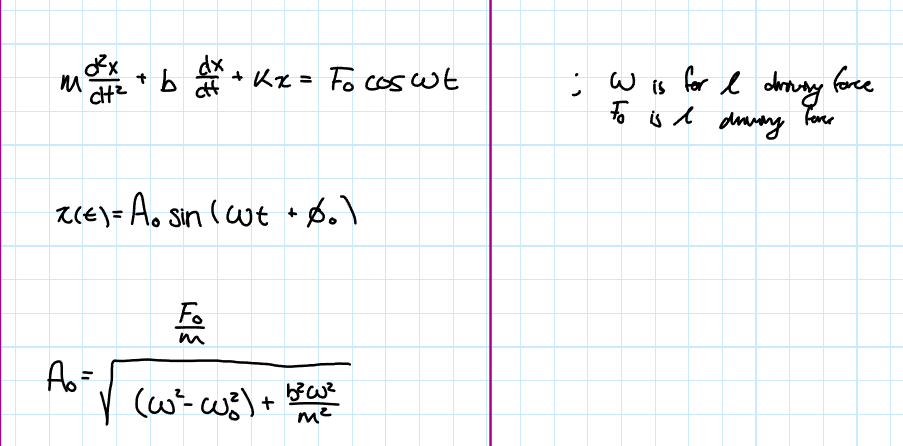
Amplitude of a Driven SHO

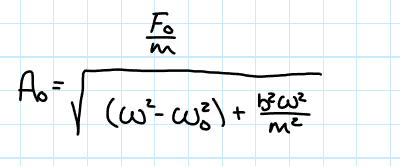
Initial Phase Shift of a Driven SHO

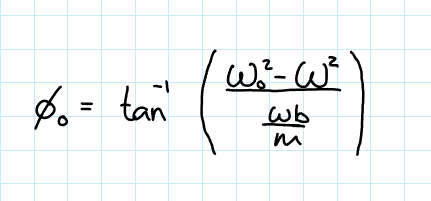
When Resonance Conditions are Met and Maximum Amplitude Condition

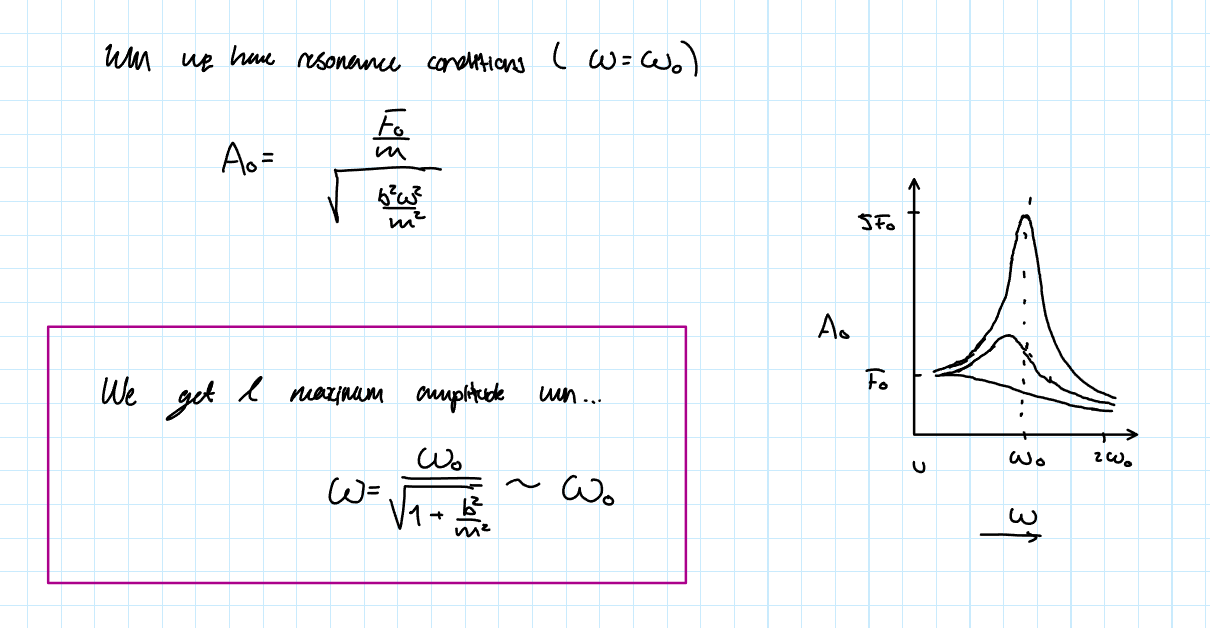
Resonant Peak and Relative Width of Resonant Peak

The resonant peak is Characterized by the Q-factor; influenced by the mass, original angular frequency, and dampening constant.

The relative width of the resonant peak is the inverse of the Q-factor