Electrical conductivity (module 1)

ch 5

classical free electron theory (postulates)

1. in metals valance electrons move freely through the crystal lattice

2. electrons form electron clouds similar to kinetic theory of gases

3. In absence off electric field electrons move randomly maintaining constant energy

4. Drude & Lorentz explained electrical conductivity using this model

5. classical gas theory concepts like- mean free path, collision time theory and average velocity can be applied to electronic gas

6. With an external electric field electrons accelerate opposite to the field with a drift velocity producing current.

Classical free electron theory derivation

relaxation time

when external electric field is applied electrons move with directional velocity called drift velocity. When field is switched off this velocity exponentially decays to zero.

Inital velocity at time t=0 is denoted by v₀. Velocity at anytime t is given by,

v=v₀e^-t/toe 

where toe is a constant, a measure of time taken for the system to relax when constraints like electric field is removed.

toe is the time taken for drift velocity to decay to 1/e to its initial value

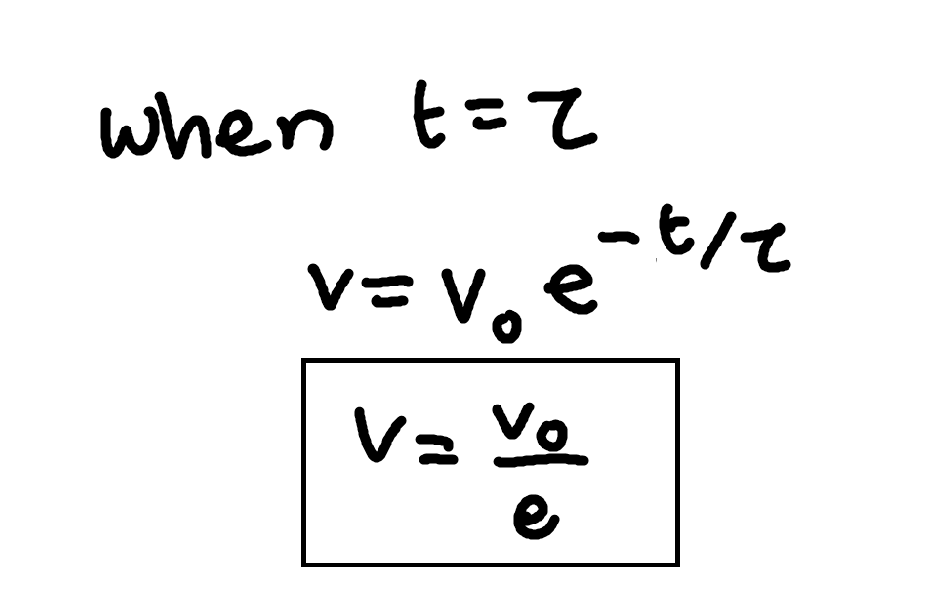
drawbacks of classical free electron theory

1. according to classical free electron theory the value of specific heat capacity is 4.5R (R=universal gas constant) but the experimental value is R (Dulong Petit law)

2. according to the theory mean free path (lamda) is 2.85nm but the value obtained experimentally is 10 times above this value.

3. according to the theory all ffree electrons in the metal take part in thermal conduction, but quantum theory and fermi dirac statistics reveal that only electrons near the fermi level taken part in themal and electrical conduction

4. Electrical conductivity of semiconductors and insulators cannot be explains using this theory

5. classic free electron theory states that magnetic susceptibility is inversely proportional to temperature while experimental values state that magnetic susceptibility is independent of temperature

6. the theory states that resistivity row directly proportion to sqrt of temperature but experimental values suggest that conductivity is directly proportional to temperature

Fermi Dirac Statistics

electrons known as fermions

in classical free electron theory electrons obey maxwell boltzman statistics

e- are indistinguishable in a solid, obey Paul’s exclusion principle

explains distribution of fermions across various energy levels for a sytem under thermal equilibrium.

Fermi Dirac Distribution

function represents the probability that a quantum state with energy E_i gets occupied by an electron
k_B- Boltzman constant

T- absolute temperature

E_F- fermi energy

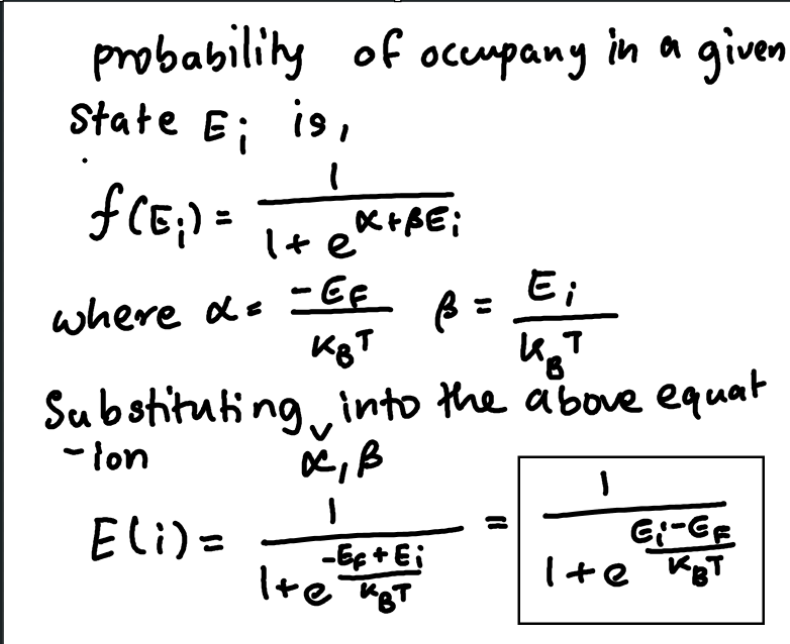
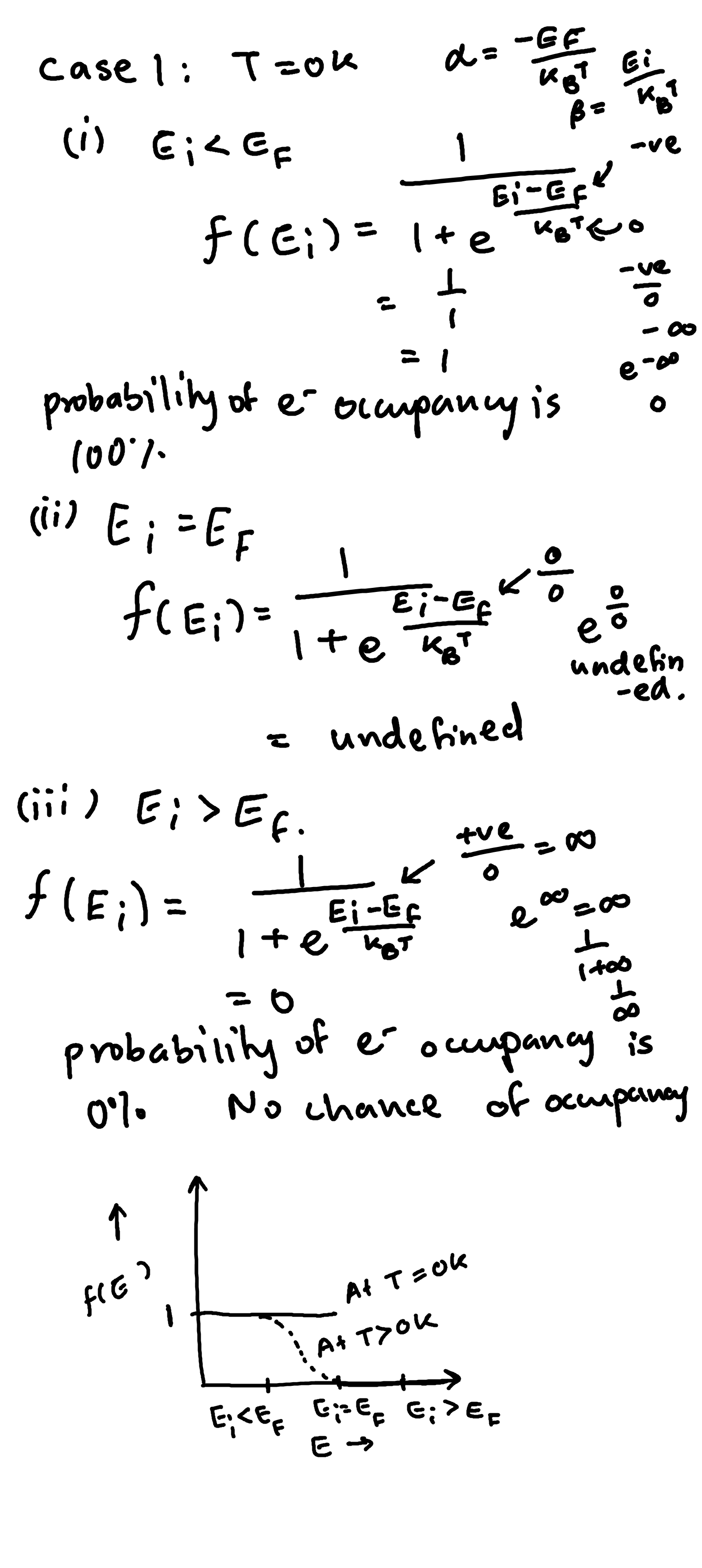
case 1

T=0K

At absolute when Ei>Ef all energy levels up to fermi level will be filled and the levels above will be empty

when Ei=Ef undefined

when Ei<Ef all energy levels up to fermi level will be empty

case 2

T>0K Ei=Ef

graph of fermi dirac distribution with temperature variation

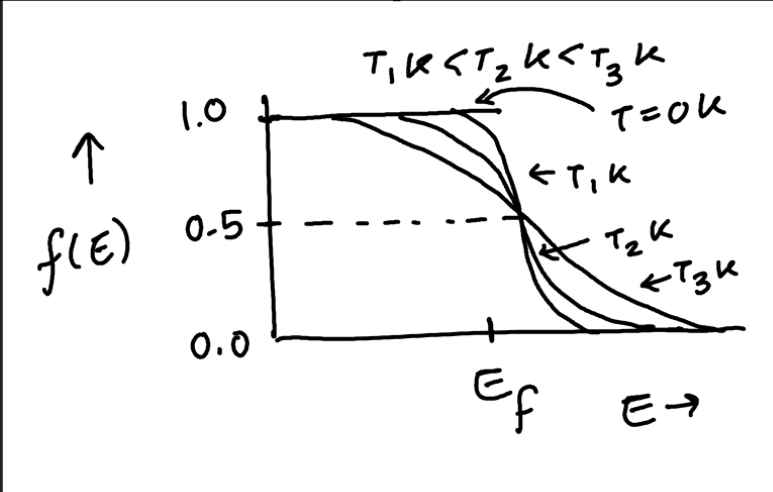
fermi energy

highest occupied energy level when T=0K

when temperature is greater than 0 probabiliy of occupancy is 1/2

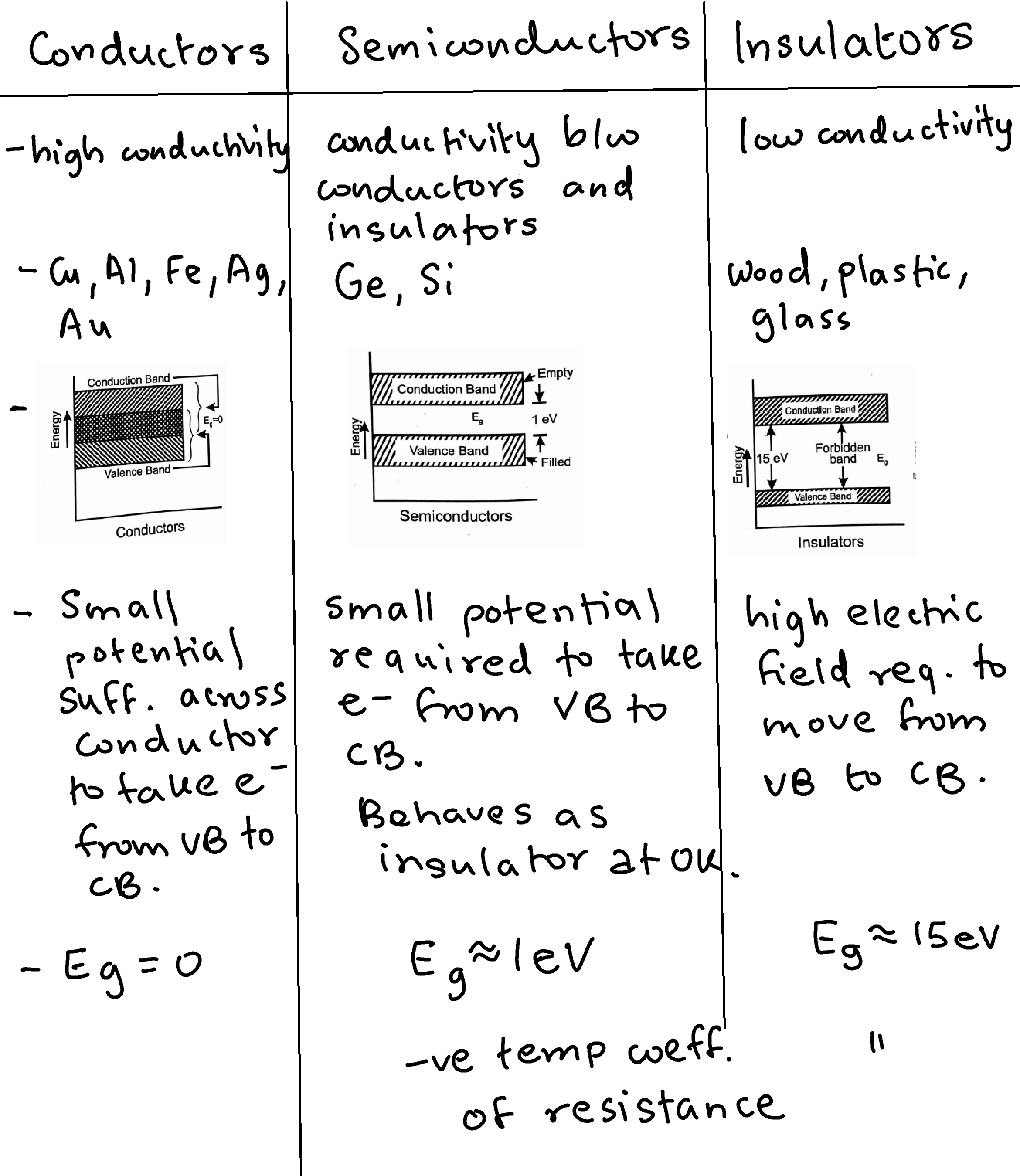
Energy bands

range of energy of electrons in a solid

forbidden energy gap

energy gap between the valence band and conduction band

Classification based on forbidden energy gap