SAT advanced math

Square of sum

a²+2ab+b²=(a+b)²

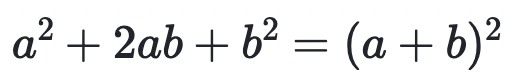
Square of difference

a²-2ab+b²=(a-b)²

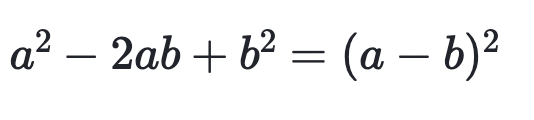
Difference of squares

a²-b²=(a+b)(a-b)

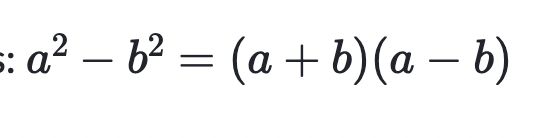
Adding and subtracting exponential expressions

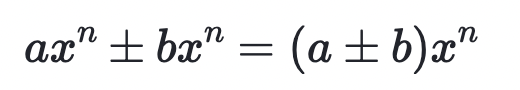
Multiplying and dividing exponential expressions

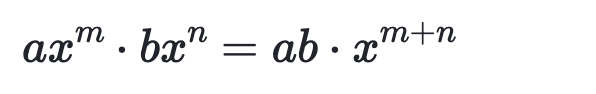
Raising an exponential expression to an exponent and change of base

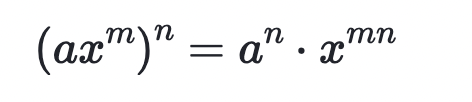
Negative exponent

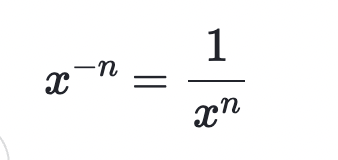
Zero exponent

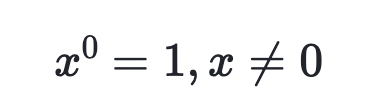
the quadratic formula

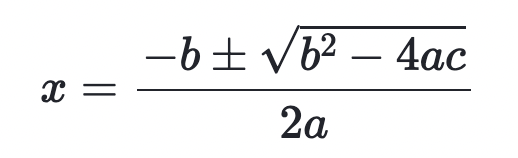
number of real solutions from the discriminant (b²-4ac)

• >0, 2 real solutions

• =0, 1 real solution

• <0, no real solution

can we divide by 0?

If a solution leads to division by \[0\], then that solution is extraneous

The radical operator calculates only

the positive square root

For the absolute value equation |ax+b |=c rewrite the equation as the following linear equations and solve them

• ax+b=c

• ax+b=-c

• Both solutions are solutions to the absolute value equation

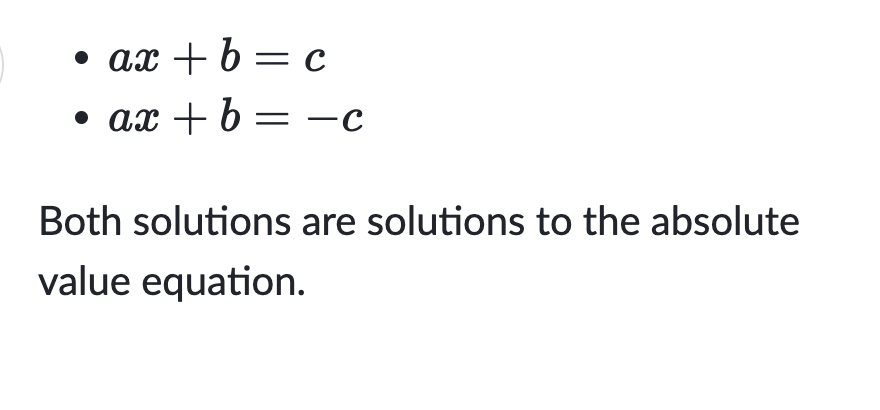
Standard form quadratic equations

Factored form quadratic equations

Vertex form quadratic equations

When we're given a quadratic function, we can rewrite the function according to the features we want to display:

Transformations

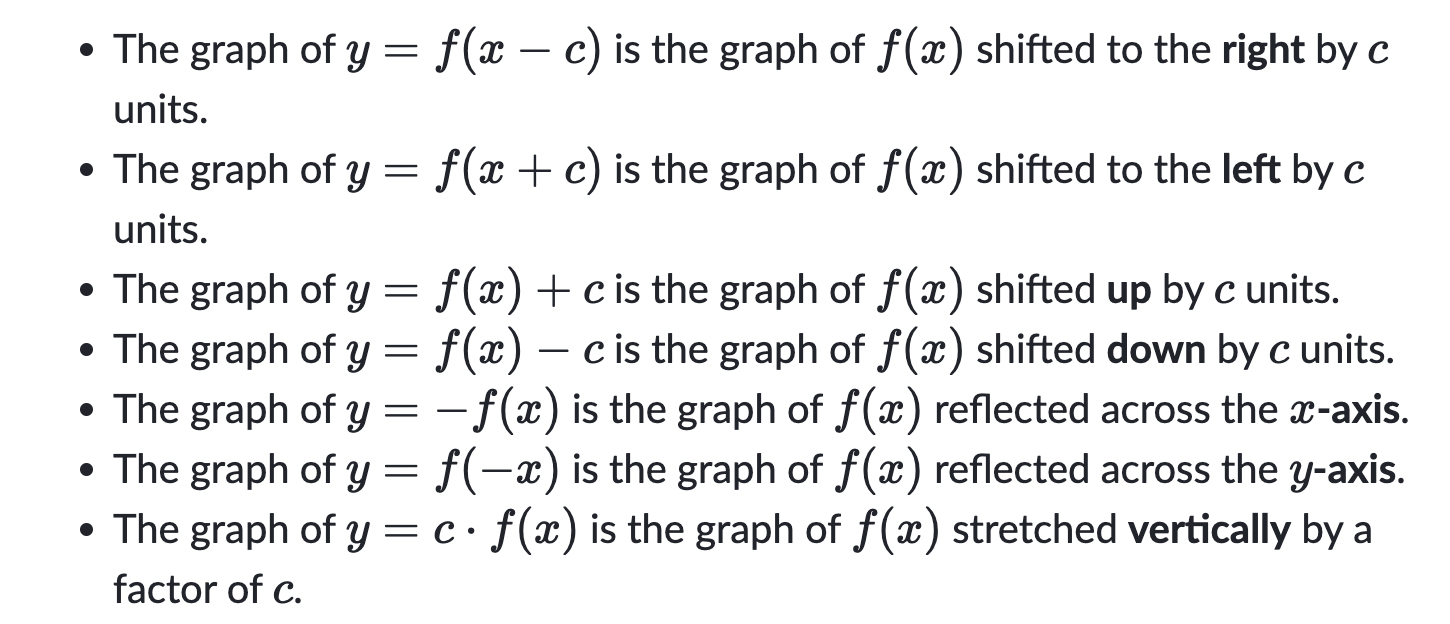
For f(x)=b^x where b is a positive real number:

• If \[b>1\], then the slope of the graph is positive, and the graph shows exponential growth. As \[x\] increases, the value of \[y\] approaches infinity. As \[x\] decreases, the value of \[y\] approaches \[0\].

• If \[0<b<1\], then the slope of the graph is negative, and the graph shows exponential decay. In this case, as \[x\] increases, the value of \[y\] approaches \[0\]. As \[x\] decreases, the value of \[y\] approaches infinity.

• For all values of \[b\], the \[y\]-intercept is \[1\].

For the highest power term axⁿ in the standard form of a polynomial function:

think of the end of precalc