Variability

Spread and Variability

• Variability - used to determine how spread out a group of scores are, or if they are bunched together

  • Synonymous (nearly the same) with terms spread and dispersion

• While central tendency describes the center of the distribution, variability describes the divergence (gap/separation) from the center

The scores are the same = no variability

A small difference between scores = small variability

A large difference between scores = large variability

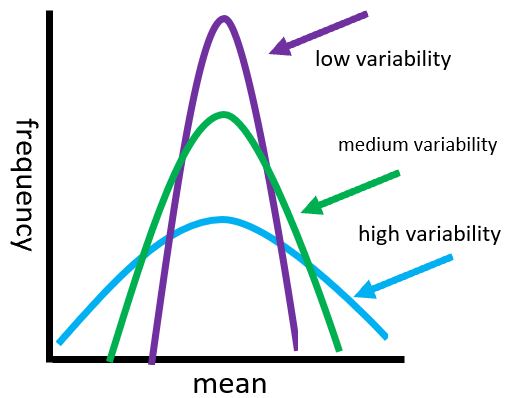
Measuring Variability

• Can utilise a few difference measures to describe variability:

  • Describes if scores are clustered or spread over distance

  • informs us of how well a score represents the entire distribution

• We do this through:

  • Range

  • Interquartile Range

  • Standard Deviation

Range

• distance between the largest score (Xmax) and the smallest score (Xmin)

FORMULA)

Range = URL Xmax - LRL Xmax

URL = Upper Real Limit

LRL = Lower Real Limit

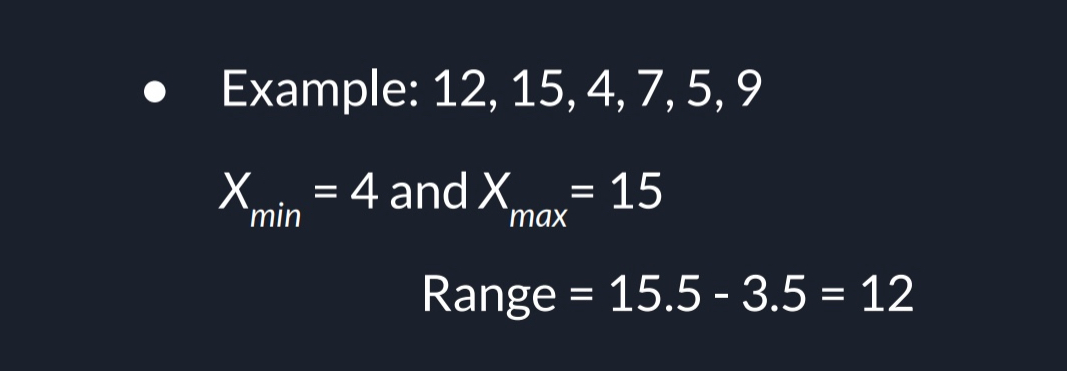
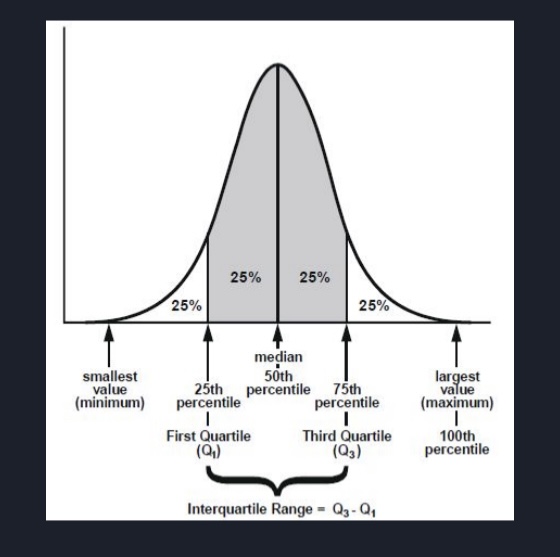
Interquartile Range (IQR)

• The range of the middle 50% of the distribution

  FORMULA) IQR = Q3 - Q1

EXAMPLE)

The data set: 1, 2, 2, 3, 3, 4, 4, 4(8th), 5(9th), 5, 5, 5, 6, 6, 6, 7

Step 1: Find the Median (Q2)

There are 16 numbers

• Middle position is between the 8th and 9th values

• 8th value = 4, 9th value = 5

• Median = (4 + 5) / 2 = 4.5

So the dataset is split into lower half (first 8 numbers) and upper half (last 8 numbers).

Step 2: Find Q1 (the median of the lower half)

Lower half: 1, 2, 2, 3(4th), 3(5th), 4, 4, 4

There are 8 numbers

• Middle is between 4th and 5th values = (3 + 3) ÷ 2 = 3

So Q1 = 3

Step 3: Find Q3 (the median of the upper half)

Upper half: 5, 5, 5, 5(4th), 6(5th), 6, 6, 7

• Middle is between 4th and 5th values = (5 + 6) ÷ 2 = 5.5

So Q3 = 5.5

Step 4: Calculate IQR

IQR = Q3 – Q1 = 5.5 – 3 = 2.5

Semi-Interquartile Range

• Half of the interquartile range

  • Semi-interquartile range = (Q3 - Q1)/2

    Semi-interquartile range = (5.5 -3)/2

• Most stable measure of variability

  • Less likely to be influenced by extreme scores; does not give a complete picture of the variability for the entire set

Standard Deviation and Variance 𝜎² / 𝜎: Population

1. Determine the distance or deviation of each score from the mean

   • FORMULA) Deviation score = X - μ

2. Square each deviation score: (X - μ)²

3. Sum of the Squared Deviations(SS): SS = ∑(X - μ)²

   • The average of these scores is the population variance

   • The variance is the average squared distance from the mean

4. Square root the variance

   • Correction for having all the squared distances

Standard Deviation and Variance s² / s: Sample

• Bias: Sample variability is always smaller than population variability

• Have to adjust for this bias

  • For the mean: Use X̄ instead of μ

  • Variability: Computation steps for the numerator are the same

    1. Find the deviation for each score: X - X̄

    2. Square each deviation: (X - X̄)²

    3. Add the squared deviations: 𝑆𝑆 = ∑(X - X̄)²

• 𝑆𝑆 = ∑(X - X̄)² is the same computation as for the population

• Adding the correction for this bias in sample variability, the denominator becomes N-1

Degrees of Freedom (df)

How many values can you choose freely before the last one is forced by the mean condition

Step 1: How many numbers do we have?

• We have 3 numbers: 2, 4, 6

  • Find MEAN:

    FIRST ∑X: 2 + 4 + 6 = 12 (this is our sum)

    THEN DIVIDE ∑X (12) by N (3): 12/3 = 4

  • MEAN = 4

Step 3: How many values we can have free?

Imagine you have 3 boxes 🟦🟦🟦

• You need to put numbers inside them

• The rule is: the mean must equal 4

That’s because: MEAN formula needs to make sense

12 (the sum)/3 (the N) = 4

EXAMPLE)

1. Pick the first number; Say you put 2 in the first box - Nothing stops you, totally free choice

2. Pick the second number; Say you put 7 in the second box - Again, free choice

3. Now what about the third box; Now the first two numbers already add up to 2 + 7 = 9, But the total has to equal 12 …

   • That means the third box is forced to be 12 − 9 = 3; (not free anymore).

Key idea:

• Box 1 = free

• Box 2 = free

• Box 3 = locked (it must make the total = 12)

So even though you have 3 numbers, only 2 are “free to vary.”

That’s why the degrees of freedom = 2.

Standard Deviation: Importance

1. Provides a measure of the typical or standard distance from the mean for a distribution

2. Allows for interpretation of individual scores

3. Common measure to describe a set of data

   • along with the mean

Standard Deviation: Transformation

• Adding or Subtracting a constant to/from each score

  • Not change the standard deviation

    Consider a distribution with μ = 40 and σ = 10 ; Add 5 points to every score

• Multiplying or Dividing each score by a constant

  • Causes the standard deviation to be multiplied or divided by the same constant

    Consider a distribution with μ = 40 and σ = 10 ; Multiply each score by 2