laborator

verificari + metoda substitutii ascendente

verificari + metoda substitutiei descendente

MEGFP functie python

MEGFP implementate pentru un sistem (cu metoda descendenta)

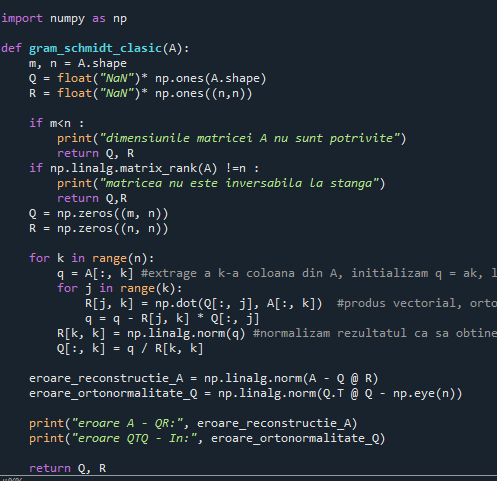
factorizare QR gram schmidt clasica algoritm python

rezolvare ecuatii normale sistem supradeterminat (m>=n) folosind MEGFP + vector eroare reziduala

import numpy as np

def MEGFP(A, b):
    eps = 10**-14
    m, n = np.shape(A)

    if m != n:
        raise ValueError("Matricea A nu este patratica.")

    if b.shape[0] != m:
        raise ValueError("Matricea A nu este compatibila cu vectorul b.")

    A = A.copy().astype(float)
    b = b.copy().astype(float)

    for k in range(n-1):
        for i in range(k+1,n):
            if A[k,k]==0 :
                raise ZeroDivisionError("Pivot nul")
            pivot = A[i,k]/A[k,k]
            A[i,k:]-=pivot*A[k,k:]
            b[i]-=pivot*b[k]
    return A, b

def desc(U,y):
    n=np.shape(y)[0]
    if U.shape[0] != U.shape[1]:
        raise ValueError("Matricea U nu este patratica.")
    if U.shape[0] != y.shape[0]:
        raise ValueError("Vectorul y nu este compatibil cu matricea U.")
    
    x= np.zeros(n)

    for i in reversed(range(n)):
        if U[i,i] == 0 :
            raise ZeroDivisionError("Zero pe diagonala in substitutia descendenta")
    suma = 0
    for j in range(i + 1, n):
        suma += U[i, j] * x[j]
        x[i] = (y[i] - suma) / U[i, i]

    return x


def rez_ec_normale_MEGFP(A, b):
    m, n = A.shape
    if m < n:
        raise ValueError("Matricea A trebuie sa aiba m >=n.")
    if np.linalg.matrix_rank(A) < n:
        raise ValueError("Matricea A nu este inversabila la stanga.")
    if A.shape[0] != b.shape[0]:
        raise ValueError("Matricea A si vectorul b nu au acelasi numar de linii.")

    AtA = A.T @ A
    Atb = A.T @ b

    U,y = MEGFP(AtA,Atb)
    x= desc(U,y)

    eroare_reziduala = b - A @ x
    norma_eroare_reziduala = (eroare_reziduala**2).sum()**0.5

    return x, norma_eroare_reziduala

rezolvare ecuatii normale sistem supradeterminat (m>=n) folosind MEGPP + vector eroare reziduala

import numpy as np

def MEGPP(A, b):
    eps = 1e-14
    m, n = np.shape(A)

    if m != n:
        raise ValueError("Matricea A nu este patratica.")
    if b.shape[0] != m:
        raise ValueError("Matricea A nu este compatibila cu vectorul b.")

    A = A.copy().astype(float)
    b = b.copy().astype(float)

    for k in range(n - 1): #  cautam pivotul maxim pe coloana k
        max_val = abs(A[k, k])
        max_row = k
        for i in range(k + 1, n):
            if abs(A[i, k]) > max_val:
                max_val = abs(A[i, k])
                max_row = i

        if abs(A[max_row, k]) < eps:
            raise ZeroDivisionError(f"Pivot nul la coloana {k}")

        if max_row != k:
            A[[k, max_row]] = A[[max_row, k]]
            b[k], b[max_row] = b[max_row], b[k]

        for i in range(k + 1, n):
            pivot = A[i, k] / A[k, k]
            A[i, k:] -= pivot * A[k, k:]
            b[i] -= pivot * b[k]

    return A, b

def desc(U,y):
    n=np.shape(y)[0]
    if U.shape[0] != U.shape[1]:
        raise ValueError("Matricea U nu este patratica.")
    if U.shape[0] != y.shape[0]:
        raise ValueError("Vectorul y nu este compatibil cu matricea U.")

    x= np.zeros(n)

    for i in reversed(range(n)):
        if U[i,i] == 0 :
            raise ZeroDivisionError("Zero pe diagonala in substitutia descendenta")
    suma = 0
    for j in range(i + 1, n):
        suma += U[i, j] * x[j]
        x[i] = (y[i] - suma) / U[i, i]

    return x


def rez_ec_normale_MEGPP(A, b):
    m, n = A.shape
    if m < n:
        raise ValueError("Matricea A trebuie sa aiba m >=n.")
    if np.linalg.matrix_rank(A) < n:
        raise ValueError("Matricea A nu este inversabila la stanga.")
    if A.shape[0] != b.shape[0]:
        raise ValueError("Matricea A si vectorul b nu au acelasi numar de linii.")

    AtA = A.T @ A
    Atb = A.T @ b

    U,y = MEGPP(AtA,Atb)
    x= desc(U,y)

    eroare_reziduala = b - A @ x
    norma_eroare_reziduala = (eroare_reziduala**2).sum()**0.5

    return x, norma_eroare_reziduala

rezolvare ecuatii normale sistem supradeterminat (m>=n) folosing MEGPPS + vector eroare reziduala

import numpy as np

def MEGPPS(A, b):
    eps = 1e-14
    m, n = np.shape(A)

    if m != n:
        raise ValueError("Matricea A nu este patratica.")
    if b.shape[0] != m:
        raise ValueError("Matricea A nu este compatibila cu vectorul b.")

    A = A.copy().astype(float)
    b = b.copy().astype(float)

    s = np.zeros(m)
    for i in range(m):
        val_max = 0
        for j in range(n):
            if abs(A[i, j]) > val_max:
                val_max = abs(A[i, j])
        s[i] = val_max
        if s[i] == 0:
            raise ValueError(f"Linia {i} este nulă – nu se poate scala.")

    for k in range(n - 1):
        cat_max = 0
        linie_pivot = k
        for i in range(k, n):
            cat = abs(A[i, k]) / s[i]
            if cat > cat_max:
                cat_max = cat
                linie_pivot = i

        if abs(A[linie_pivot, k]) < eps:
            raise ZeroDivisionError(f"Pivot nul la coloana {k}")

        if linie_pivot != k:
            A[[k, linie_pivot]] = A[[linie_pivot, k]]
            b[k], b[linie_pivot] = b[linie_pivot], b[k]
            s[k], s[linie_pivot] = s[linie_pivot], s[k]

        for i in range(k + 1, n):
            factor = A[i, k] / A[k, k]
            for j in range(k, n):
                A[i, j] -= factor * A[k, j]
            b[i] -= factor * b[k]

    return A, b

def desc(U,y):
    n=np.shape(y)[0]
    if U.shape[0] != U.shape[1]:
        raise ValueError("Matricea U nu este patratica.")
    if U.shape[0] != y.shape[0]:
        raise ValueError("Vectorul y nu este compatibil cu matricea U.")

    x= np.zeros(n)

    for i in reversed(range(n)):
        if U[i,i] == 0 :
            raise ZeroDivisionError("Zero pe diagonala in substitutia descendenta")
    suma = 0
    for j in range(i + 1, n):
        suma += U[i, j] * x[j]
        x[i] = (y[i] - suma) / U[i, i]

    return x


def rez_ec_normale_MEGPP(A, b):
    m, n = A.shape
    if m < n:
        raise ValueError("Matricea A trebuie sa aiba m >=n.")
    if np.linalg.matrix_rank(A) < n:
        raise ValueError("Matricea A nu este inversabila la stanga.")
    if A.shape[0] != b.shape[0]:
        raise ValueError("Matricea A si vectorul b nu au acelasi numar de linii.")

    AtA = A.T @ A
    Atb = A.T @ b

    U,y = MEGPP(AtA,Atb)
    x= desc(U,y)

    eroare_reziduala = b - A @ x
    norma_eroare_reziduala = (eroare_reziduala**2).sum()**0.5

    return x, norma_eroare_reziduala

rezolvare ecuatii normale sistem supradeterminat (m>=n) folosing cholesky + vector eroare reziduala

import numpy as np

def cholesky(A):
    """
    Performs Cholesky decomposition of a symmetric positive definite matrix A.
    Returns L such that A = L @ L.T
    """
    n = A.shape[0]
    L = np.zeros_like(A)

    for i in range(n):
        for j in range(i + 1):
            suma = sum(L[i, k] * L[j, k] for k in range(j))
            if i == j:
                L[i, j] = np.sqrt(A[i, i] - suma)
            else:
                L[i, j] = (A[i, j] - suma) / L[j, j]
    return L

def substitutie_asc(L, b):
    """ Solves Ly = b using forward substitution """
    e= 10**-14
    l= np.shape(A)[0]
    c= np.shape(A)[1]

    n = len(b)
    y = np.zeros(n)
    if l!= n :
        raise ValueError("Sistemul nu este compatibil")
    if l!= c :
        raise ValueError("Matricea A nu este patratica")
    for i in range(0,l-1):
        for j in range(i+1,l):
            if abs(A[i][j])>e:
                raise ValueError("Matricea A nu este inferior triunghiulara")
    if np.linalg.det(A)< e:
        raise ValueError("Matricea A are determinant nul")

    for i in range(n):
        suma = sum(L[i, j] * y[j] for j in range(i))
        y[i] = (b[i] - suma) / L[i, i]
    return y

def substitutie_desc(U, y):
    """ Solves Ux = y using backward substitution """
    e = 10 ** -14
    l = np.shape(U)[0]
    c = np.shape(U)[1]

    n = len(y)
    y = np.zeros(n)
    if l != n:
        raise ValueError("Sistemul nu este compatibil")
    if l != c:
        raise ValueError("Matricea A nu este patratica")
    for i in range(1,l):
        for j in range(i):
            if abs(A[i][j]) > e:
                raise ValueError("Matricea A nu este superior triunghiulara")
    if np.linalg.det(A) < e:
        raise ValueError("Matricea A are determinant nul")
    n = len(y)
    x = np.zeros(n)
    for i in reversed(range(n)):
        suma = sum(U[i, j] * x[j] for j in range(i + 1, n))
        x[i] = (y[i] - suma) / U[i, i]
    return x

def rez_ec_normale_Cholesky(A, b):
    """
    Solves the least squares problem Ax = b using Cholesky factorization.
    """
    m, n = A.shape

    if m < n:
        raise ValueError("Matricea A trebuie sa aiba m ≥ n.")
    if np.linalg.matrix_rank(A) < n:
        raise ValueError("Matricea A nu este inversabila la stanga.")
    if A.shape[0] != b.shape[0]:
        raise ValueError("Matricea A si vectorul b nu au acelasi numar de linii.")

    AtA = A.T @ A
    Atb = A.T @ b

    L = cholesky(AtA)
    y = substitutie_asc(L, Atb)
    x = substitutie_desc(L.T, y)

    eroare_reziduala = b - A @ x
    norma_eroare = np.sqrt((eroare_reziduala**2).sum())

    return x, norma_eroare

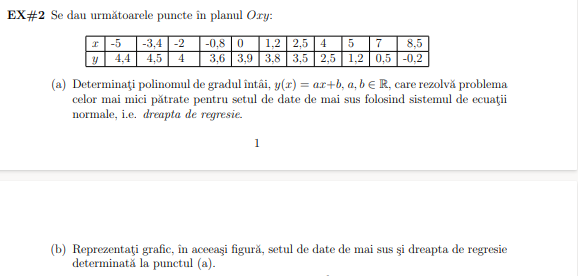
grafice + metoda celor mai mici patrate

import numpy as np
import matplotlib.pyplot as plt

# === Your Cholesky-based least squares solver (as defined earlier) ===
def cholesky_decomposition(A):
    n = A.shape[0]
    L = np.zeros_like(A)
    for i in range(n):
        for j in range(i + 1):
            suma = sum(L[i, k] * L[j, k] for k in range(j))
            if i == j:
                L[i, j] = np.sqrt(A[i, i] - suma)
            else:
                L[i, j] = (A[i, j] - suma) / L[j, j]
    return L

def forward_substitution(L, b):
    n = len(b)
    y = np.zeros(n)
    for i in range(n):
        suma = sum(L[i, j] * y[j] for j in range(i))
        y[i] = (b[i] - suma) / L[i, i]
    return y

def backward_substitution(U, y):
    n = len(y)
    x = np.zeros(n)
    for i in reversed(range(n)):
        suma = sum(U[i, j] * x[j] for j in range(i + 1, n))
        x[i] = (y[i] - suma) / U[i, i]
    return x

def rez_ec_normale_Cholesky(A, b):
    m, n = A.shape
    if m < n:
        raise ValueError("Matricea A trebuie sa aiba m ≥ n.")
    if np.linalg.matrix_rank(A) < n:
        raise ValueError("Matricea A nu este inversabila la stanga.")
    if A.shape[0] != b.shape[0]:
        raise ValueError("Matricea A si vectorul b nu au acelasi numar de linii.")
    AtA = A.T @ A
    Atb = A.T @ b
    L = cholesky_decomposition(AtA)
    y = forward_substitution(L, Atb)
    x = backward_substitution(L.T, y)
    residual = b - A @ x
    norm = np.sqrt((residual**2).sum())
    return x, norm

# === (a) Solve regression line ===
x_data = np.array([-5, -3.4, -2, -0.8, 0, 1.2, 2.5, 4, 5, 7, 8.5])
y_data = np.array([4.4, 4.5, 4, 3.6, 3.9, 3.8, 3.5, 2.5, 1.2, 0.5, -0.2])

# Build A matrix for linear regression y = ax + b
A = np.column_stack((x_data, np.ones_like(x_data)))
b = y_data

coeffs, error = rez_ec_normale_Cholesky(A, b)
a, b_intercept = coeffs

print(f"Regresie: y(x) = {a:.4f}x + {b_intercept:.4f}")
print(f"Norma erorii reziduale: {error:.4f}")

# === (b) Plot regression line and data ===
x_line = np.linspace(min(x_data), max(x_data), 200)
y_line = a * x_line + b_intercept

plt.figure(figsize=(8, 5))
plt.scatter(x_data, y_data, color='blue', label='Puncte date')
plt.plot(x_line, y_line, color='red', label=f'Regresie: y = {a:.2f}x + {b_intercept:.2f}')
plt.title('Regresie liniară prin metoda celor mai mici pătrate')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()