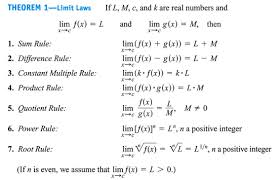Analysis H - Limits and Calculus Important Stuff

For the cram

AROC

Over interval [a, b]

IROC

f’(x) = dy/dx

Formal definition of a limit

Types of discontinuities

Points where a function is not continuous, including removable(hole) , jump(step), and infinite(vertical asymptote) discontinuities.

Variables for limits with infinites

x → ∞ use D and attempt to find D in terms of epsilon.

lim f(x) = ∞ use E and attempt to find delta in terms of E such that f(x) is greater than E when x is within delta of c.

Differentiable

A function is deemed differentiable at a point if it has a well-defined tangent line at that point. (if it has a derivative)

Continuity

Intermediate Value Theorem (IVT)

States that for any value between f(a) and f(b), there exists at least one c in (a, b) such that f(c) equals that value, given that f is continuous on [a, b].

Formal Definition of Derivative at a Point

Formal Definition of the Derivative

Examples of when there is no derivative

include points of non-differentiability, such as cusps, vertical tangents, or discontinuities.

Derivative of trig functions

cosx → -sinx
sinx → cosx

secx → secx tanx
cscx → -cscx cotx

cotx → -csc²x

tanx → sec²x

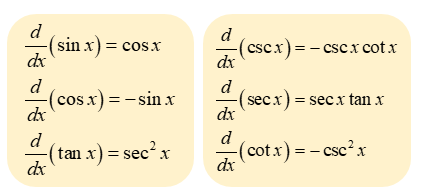
Laws of limits