ch 3- discrete random variable

Random Variable (RV)

Mapping from outcomes of a sample space to real numbers; not random, not a variable.

Range of RV

Set of all possible values the random variable can take.

Discrete Random Variable (DRV)

An RV whose range is a countable set (finite or countably infinite).

Continuous Random Variable (CRV)

An RV whose range is an interval (uncountable; infinitely many values).

Probability Mass Function (PMF)

You use a Probability Mass Function when you’re working with a discrete random variable- exact outcome

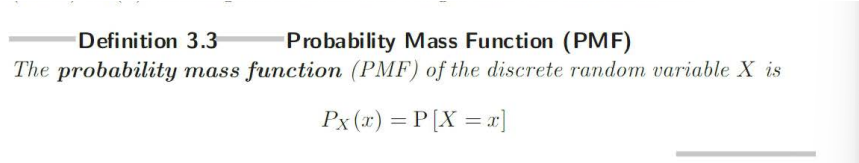
Family of DRVs

Bernouili, Binomial, Geometric, Poisson, Discrete, Uniform

Bernoulli RV

measures Success (1) or Failure (0).

Bernoulli PMF

The mathmetic function

Geometric RV

Counts number of trials until the first success.

Geometric PMF

mathmetical form

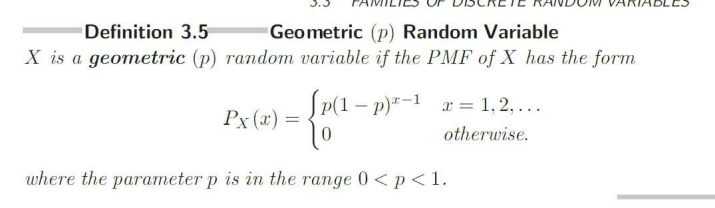
Pascal/Negative Binomial RV

Counts number of trials until the r-th success occurs.

Negative Binomial PMF

The PMF (Probability Mass Function) is the formula that gives the probability that the random variable equals a specific value.

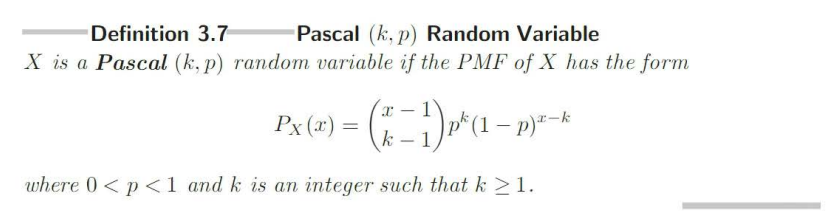
Negative Binomial Parameters

r = number of successes, p = probability of success.

Discrete Uniform RV

All outcomes equally likely from finite set.

Discrete Uniform PMF

Poisson RV

Models number of events in fixed interval when events occur independently at constant rate.

Poisson PMF

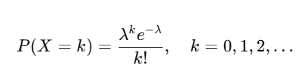
Poisson Parameter

λ = average rate of occurrence.

Cumulative Distribution Function (CDF)

F(x) = P(X ≤ x); probability that X takes on a value less than or equal to x.

Expected Value (Geometric)

E[X] = 1/p.

Expected Value (Binomial)

E[X] = n p.

Expected Value (Pascal/Neg. Binomial)

E[X] = k/p.

Expected Value (Discrete Uniform)

E[X] = (k + l)/2.

Variance

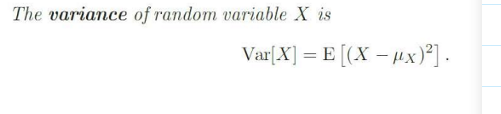
Standard Deviation

σ_X = √Var(X).

Interpretation of Variance

Small variance = values close to mean; large variance = values far from mean.

Variance in plain words

Average squared distance from the mean.

Covariance

Cov(X,Y) = E[(X-μX)(Y-μY)]; measures linear relationship between X and Y.

Independence vs. Correlation

Independence ⇒ Cov=0, but Cov=0 does NOT necessarily imply independence.