Week 9: correlational analysis

What does bivariate mean?

two variable/participant

What is a positive correlational relationship?

When a goes up, b goes up

What is a negative correlational relationship?

When a goes up, b goes down

What has happened if i have a perfect relationship?

I’ve measured the same thing two different ways OR I’ve cheated

What is the purpose of a correlation analysis?

To determine:

1. whether there is a linear relationship between two variables

2. The direction of the relationship

3. The strength of the relationship

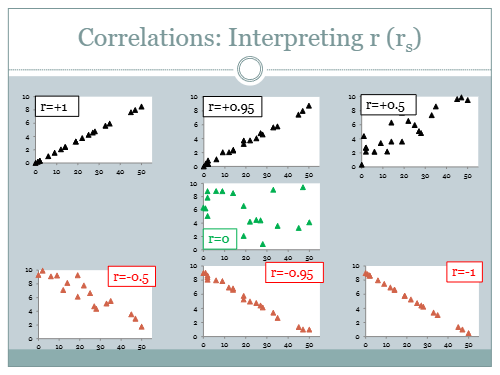
What is the pearson correlation coefficient

r

Value between -1 and 1

Positive value = positive correlation

Negative value = negative correlation

The stronger the relationship, the closer the r is to ± 1

measures how close the data is to the line of best fit

What is the spearman correlation coefficient

rs (s is subscript)

What makes correlational analysis distinct from other analyses?

Correlation makes no distinction between the dependent and independent variable

Correlation coefficients DO NOT change if we change the units of measurement

No manipulation occurring

How do we approach linear and non-linear relationships?

Linear: measuring correlations ok

Non-linear: measuring correlation does not make sense, might need to transform data

r value of 0 = no linear relationship between 2 variables, not necessarily no relationship at all

Outline the pearson r value and its pros and cons

Calculated directly from raw scores

Suitable for data on an interval or ratio scale

Highly affected by outliers

Not suitable for skewed data

More powerful than the spearman r

Outline the Spearman rs value and its pros and cons

Calculated from the ranking of the raw scores

Suitable for data on an ordinal scale

Marginally affected by outliers

Suitable for skewed data

If it looks a bit weird, go for Spearman

Outline the chi-square test for goodness of fit

x²

Use on unrelated data- every participant yields data for only one category

Used to answer questions about the proportions of a population distribution

Used to compare different levels of ONE variable
Compares the sample proportions to population proportions as specified by the null hypothesis

Non-parametric, can use with data of lower levels but not ratio or interval

Outline parametric tests

Both types of tests are available to test for significant differences between data sets

Make assumptions about population parameters (are distribution dependent)

Require interval or ratio scale data

Violation of test assumptions lead to erroneous interpretations of the data

Outline non-parametric tests

Make no assumptions about population parameters (are distribution free)

Use data at nominal level

Not as powerful, can fail to detect differences

More robust, can utilise a greater range of data

outline the chi squared test of independence

are two separate variables independent or associated?

still mutually exclusive

H0 = the two variables are completely independent from each other

H1 = there is a relationship between x and y, or, the proportion of x to y is different in these categories