hat notation and parallel vectors

coursera. Introduction to Linear Algebra Module 1 Hat notation and parallel vectors

how we denote the lenght (or magnitude) of a vector?

we said the vectors are characterized by 3 things: magnitude (or lenght), direction and sense

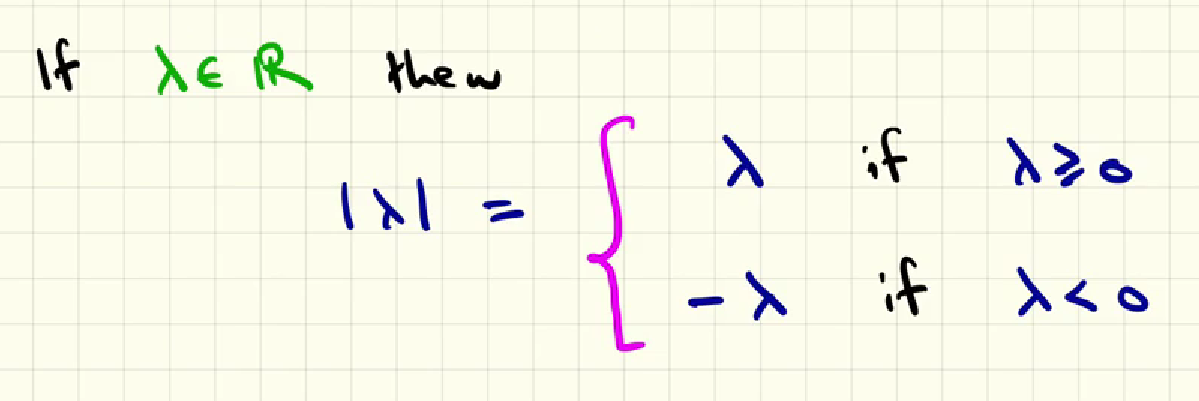
The lenght (in italiano il modulo) is denoted by |v| where v is the vector and the two vertical line denote the “magnitude” (in italiano il modulo o valore assoluto).

recalling the idea of “module” for real numbers, what are the possible value of |lambda|?

as we can se this was the very simple and first things we were tought when we learnt the module of a real number.

For example if lambda is -3, the module would be 3 since it’s less than 0

|v|*|2| is equal to |2v|?

yes since this in the image is the rule of scalars multilplication when we use module vectors

|-lambda*v | is equal to |lambda*v|

yes, since the module return the lenght of vector with no consideration for the sign

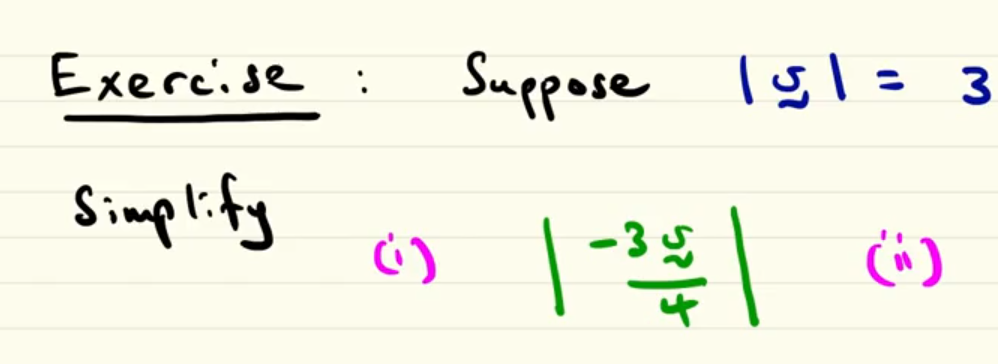
how to resolve this exercise?

here the solution

how to solve this simple problem?

here the solution

what is a unit vector?

A unit vector is a vector with a magnitude (or length) of exactly 1. It essentially represents a direction without any scaling factor. Unit vectors are often used to define directions in space and are sometimes called normalized vectors. 

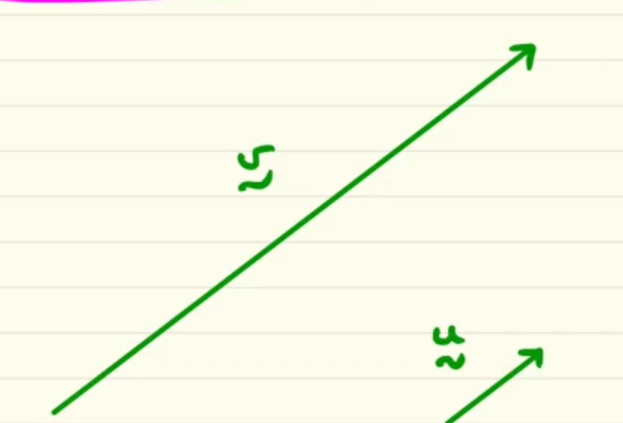
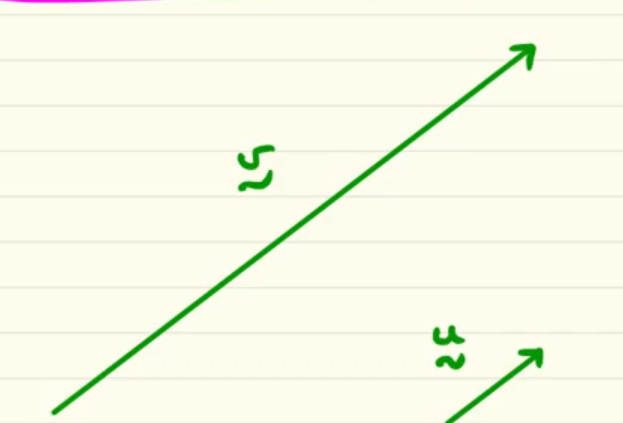
in this case which is the unit vector?

since the unit vector is often denoted by u, this is the unit vector of the vector v… we can see that v is kind of 4 times the lenght of u and both have the same direction and sense

how we define a unit vector starting from a non zero vector v?

To define a unit vector from any non-zero vector v, you simply divide the vector by its own magnitude (or module). This process is called “normalization”… remember that a unit vector i often called “normalized vector”.

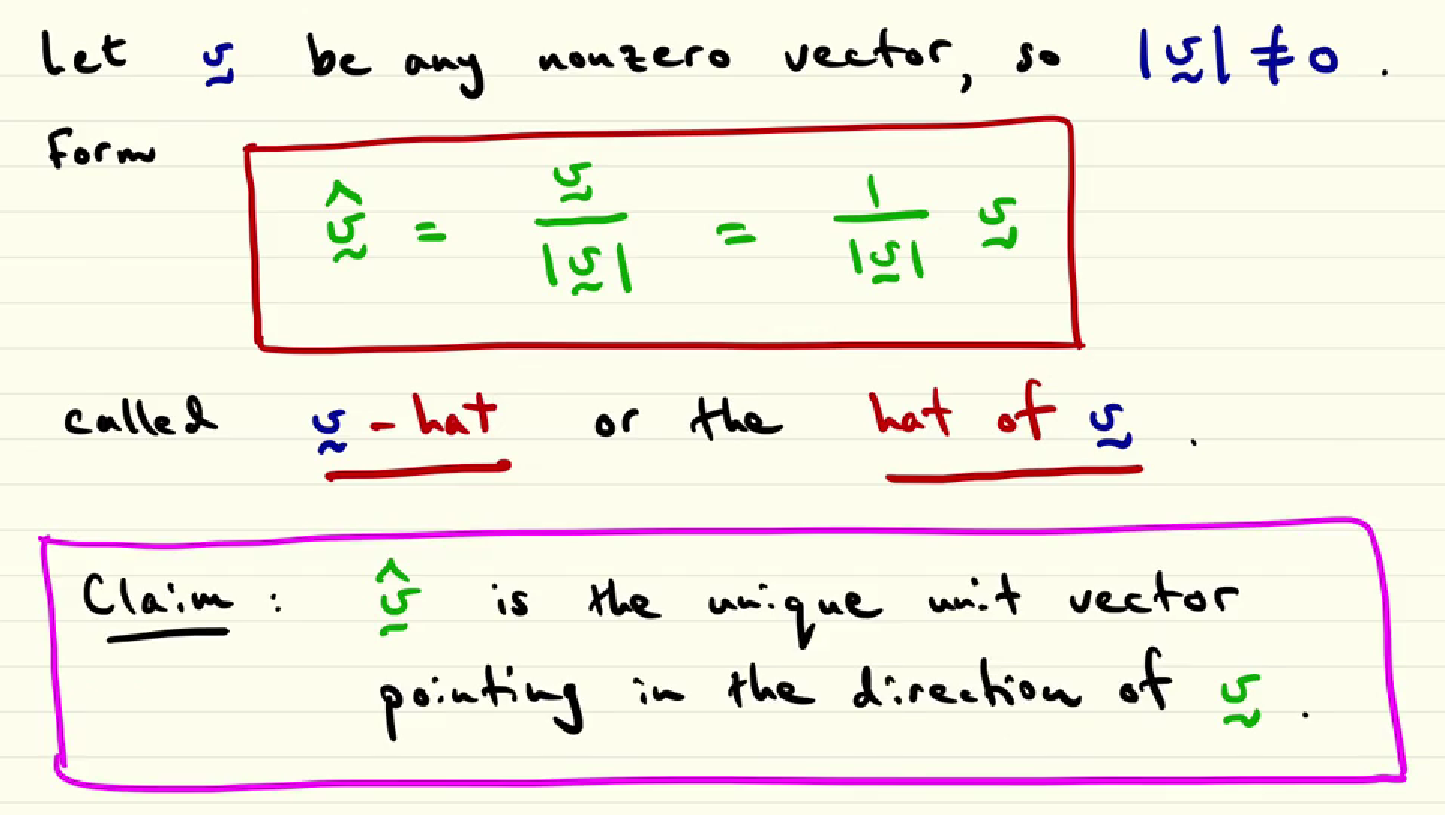
an exmple of how to define a unit vector of a vector

when are two vectors parallel?

when they point in the same or opposite directions

the 0 vector is parallel to which vector/s?

Since the 0 vector point in every direction, it is parallel to all vectors. It’s quite obvious but non that obvious graphically speaking, in fact a 0 vector is something like a dot, it doesn’t have direction but exist.

explain the terms in this equation

here we have a vector “v” and on the second term the same vector but decomposed into magnitude |v| and direction (v hat).

So as we know |v| identify just the lenght of the v vector without considering its direction, while “v-hat” denote the unit vector or normalized vector of v, which represent its direction but not considering its lengh.

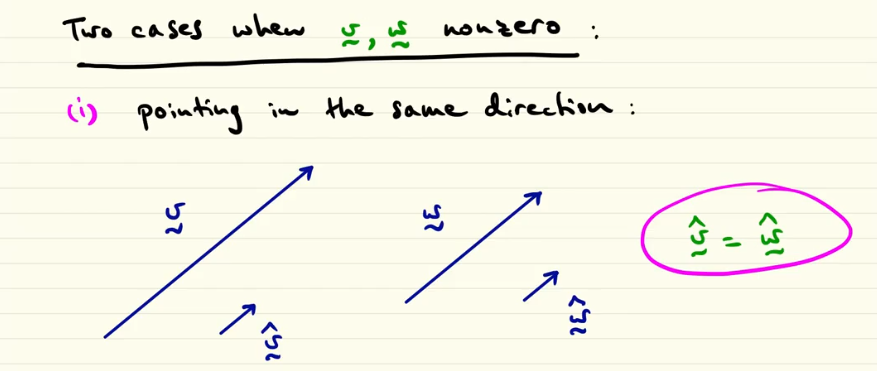
if v and w are two vector that point in the same direction (are parallel) how we can define the both of them using the extensive notation that use |module| and unit vector?

Since they are parallel they have the same “unit vector” (direction) but different lenght (module)… here labda define the ration between their lenght.

how to write the equation of two vectors that have opposite direction?

since they have opposite direction v hat is equals to minus w hat