Sample Size - PPT

Outcomes: understand the relationship between statistical power and sample size; know the importance of sample size in research; know the basic factors that should be considered in a sample size calculation; be able to carry out a simple size calculation; know some strategies for reducing required sample size

What is sample size estimation?

the problem of determining the number of subjects required to give sufficient probability of detecting an effect, where there is an effect; to give sufficient statistical power of detecting an effect

When should sample size be decided upon?

at the beginning of a study

Downsides of insufficient sample size (too small or too big)

• too few many patients has insufficient power to detect a clinically relevant treatment effect

• won’t advance science

• waste of money

• waste of patient’s time

• exposes patients to unnecessary risk and discomfort

• exposes more patients to risk and/or discomfort than necessary

• will take longer to complete than necessary

• uses more resources than necessary

In a clinical trial, sample size is determined to what?

determined to give sufficient statistical power to detect an intervention effect of a given size as measured on the primary endpoint

Alternative hypothesis usually states what?

that there is a treatment effect or a difference between treatments

If the alternative hypothesis is true…

• the test statistic does not follow the assumed distribution under the null hypothesis

• test statistic distribution differs from that assumed under null hypothesis

What is statistical power?

• probability of rejecting the null hypothesis when the alternative hypothesis is true

• probability of obtaining a test statistic in the ‘rejection region,’ when the true effect is of a given magnitude and direction

What might affect statistical power?

• bigger effect size —> increase statistical power

• small difference between distribution —> smaller statistical power

• sample size increases —> statistical power increases

• sample size decreases —> statistical power decreases

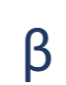
This symbol is what?

the probability of a type II error (false negative - failing to reject the null hypothesis when the research hypothesis is true)

What happens to type II errors when sample size increases?

Type II error rate decreases

What does 80% power for detecting an effect of size E mean?

It means there is an 80% probability of correctly rejecting the null hypothesis when the effect size E is present.

if the alternative hypothesis is true, with a specified effect size E, there is an 80% probability our study will reject the null hypothesis (true positive)

Factors that affect sample size?

• analysis method

• anticipated dropout

• allocation ratio

• statistical power

• effect size

• variability in endpoint/ event rate

• alpha —> type I error rate

type I error (false positive) rate = ??

= significance level (alpha)

When planning sample size, you need to decide on what?

the size of effect you would like the study to have power to detect

What is MCID?

• minimal clinically important difference

• the size of effect that would be clinically meaningful to a patient

What will happen to statistical power of a study when the true effect size increases?

null and alternative sampling distributions move further apart

What’s Cohen’s d?

a measure of effect size that indicates the standardized difference between two means (cohen’s d = difference in means/ standard deviation

factors that increase sampling variability increase what?

increase required sample size

for a numeric endpoint, what happens with sampling variability and sample size?

• higher standard deviation of the primary endpoint increases sampling variability

• a larger sample size is required to achieve a desired level of statistical power

• need to estimate variability for each treatment arm when planning a study

For a categorical endpoint, what happens with sampling variability and sample size?

• the closer the anticipated event rates (proportions) are to 0.5 or 50%, the higher the sampling variability

• a larger sample size is required to achieve desired level of statistical power

Cohen recommends what statistical power?

at least 0.8 or 80%

What is allocation ratio?

• relative size of study groups

• statistical power is usually maximized for an allocation ratio of 1

what is the formula for sample size adjusted for dropout?

n/ (1-D)

• n=original estimated sample size required

• D=proportion of patients that will be lost to follow-up

strategies for reducing sample size

• choose a numeric outcome

• use a paired design

• don’t choose an unnecessarily small effect size

• improve precision in outcome variables

• use a direction (one-sided) hypothesis test

• use balanced group sizes (equal allocation to all treatment arms)

steps for sample size calculation (8)

• decide on type of hypothesis test

• decide on significance level

• estimate outcome variability/ event rate

• decide on appropriate effect size

• set allocation ratio

• choose desired level of statistical power

• calculate sample size required to achieve desired level of power, given other choices

• adjust for anticipated dropout rate