Physics AQA A-Level Section 2 Waves and Optics: Chapter 4: Waves

What are electromagnetic waves?

Oscillating electric and magnetic fields that propagate through space without need for a medium (Vibrating electric field → Vibrating magnetic field → Vibrating electric field etc.)

What are longitudinal waves?

Waves in which the direction of vibration of the particles is parallel to the direction of the propagation of the waves

What are some examples of longitudinal waves?

• Sound waves

• Primary Seismic waves

• Compression waves on a slinky

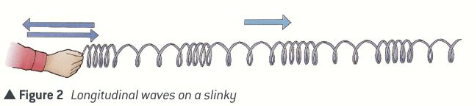
What are the particle-dense areas of longitudinal waves called?

Compressions

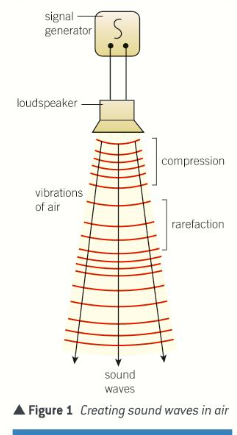
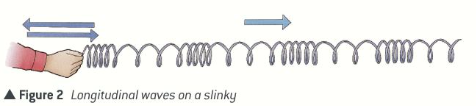
What are the non-particle-dense areas of longitudinal waves called?

Rarefactions

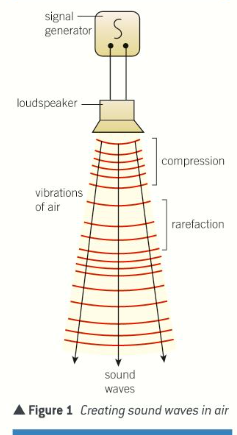
What are transverse waves?

Waves in which the direction of vibration of particles is perpendicular to the propagation of the waves

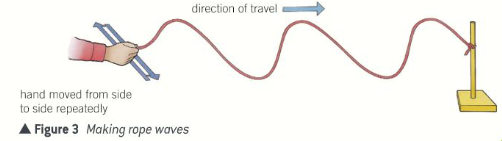
What are some examples of transverse waves?

• Electromagnetic waves

• Secondary seismic waves

• Waves on a string or wire

When is a transverse wave said to be plane-polarised?

When the direction of vibrations and the propagation is limited to one plane only

What waves cannot be polarised?

Longitudinal

What happens when unpolarised light is passed through a polaroid filter?

The transmitted light is polarised, as the filter only allows through light which vibrates in a certain direction according to the alignment of its molecules

What happens when unpolarised light is passed through two polaroid filters?

The transmitted light intensity changes if one polaroid is turned relative to the other one

When transmitted light intensity is at a minimum, what are polaroid filters said to be?

‘crossed’

Why is light intensity at a minimum when the filters are crossed?

The polarised from the first filter cannot pass through the second filter as the alignment of molecules in the second filter is at 90° to the alignment of molecules in the first filter

What is the plane polarisation of electromagnetic waves defined as?

It is defined as the plane in which the electric field oscillates in

How do polaroid sunglasses reduce the glare of light reflected by water or glass?

The reflected light is polarised and the intensity is reduced when it passes through the polaroid sunglasses

What is meant by the displacement?

Distance and direction of a vibrating particle from equilibrium position

What is the definition of equilibrium?

A position of zero displacement

What is the definition of amplitude?

The maximum displacement of a vibrating particle

What is the definition of wavelength?

The least distance between two adjacent vibrating particles with the same displacement and velocity at the same time

What is the definition of one complete cycle of a wave?

From an area of Maximum displacement to the next maximum displacement (peak to peak, trough to trough)

What is the definition of a period of a wave?

The time for one complete wave to pass a fixed point

What is the definition of the frequency of a wave?

The number of cycles of vibration of a particle per second, or the number of complete waves passing a point per second measured in Hz

How does frequency affect wavelength?

The higher the frequency, the shorter the wavelength

What is the equation between frequency and time period?

f=1/T

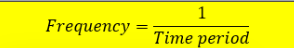
If waves travel at a constant speed, how far does the peak of a wave travel in one second?

One wavelength

What’s the equation to link distance, speed and time?

Distance = speed/time

What’s the equation to calculate wave speed using wavelength and time period?

c=λ/T

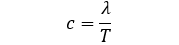
What’s the wave equation?

c=fλ

What is the phase of a vibrating particle at a certain time?

The fraction of a cycle it has completed since the start of the cycle

What is the definition of phase difference between two vibrating particles at the same frequency?

The fraction of a cycle between the two vibrating particles measured in degrees or radians

How many degrees and radians is one wave cycle?

360 degrees (2π radians)

What’s the equation for phase difference in radians?

2πd/λ

What are wavefronts?

Lines of constant phase (e.g crests)

How does the direction of a wave compare with the wavefront?

The direction of a wave is perpendicular to the wavefront

What is the definition of reflection?

The return of waves from a surface

What is the angle of incidence equal to when an incident ray is reflected by a plane mirror?

Angle of incidence = Angle of reflection

Where is a normal line drawn?

Perpendicular to the surface

What is the definition of refraction?

The change of direction of a wave when it crosses a boundary where its speed changes

What happens when a wave travels across a boundary where its speed changes?

It’s wavelength also changes

What happens when wavefronts are incident to the boundary at a non-zero angle?

They change direction as well as speed

What is the definition of diffraction?

The spreading out of waves on passing through a gap or near an edge

How does the size of a satellite dish affect the strength of its signal and its ability

What is a wavelet?

A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times.

Why are the waves diffracted on passing through the gap?

• Consider each point on the wavefront as a secondary emitter of wavelets

• The wavelets from the points along the wavefront only travel in the direction the wave is travelling and not the reverse direction

• They combine to form new wavefronts, spreading beyond the gap

How does the size of the satellite dish affect the strength of the signal and the focus of the signal?

• As the dish gets bigger, The stronger the signal it can receive because more radio waves are reflected off the dish onto the aerial.

• A bigger dish reflects the radio waves to a smaller focus because it diffracts the waves less. So the dish needs to be aligned more carefully than a smaller dish

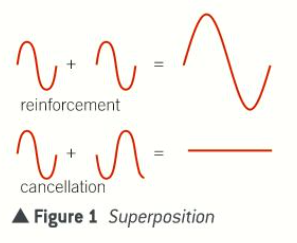
What is the definition of superposition?

At the point where waves meet, they combine for an instant before moving apart

What is the principle of superposition?

When two waves meet, the total displacement at a point is equal to the sum of the individual displacement at that point

What happens when a crest meets a crest and a trough meets a trough?

• When a crest meets a crest, a super crest is created - the two waves reinforce each other

• When a trough meets a trough, a super trough is created - the two waves reinforce each other

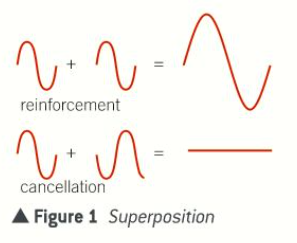
What happens when a trough meets a peak?

• If they are the same amplitude, then the resultant displacement is zero

• If they are different amplitudes, the resultant is called a minimum

When are stationary waves formed on a rope?

If two people send waves continuously along a rope from either end.

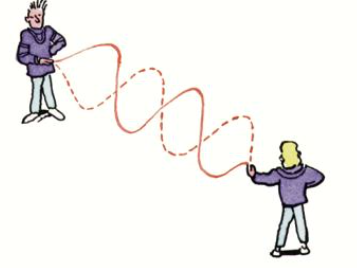
What are the two sets of waves on either side of a stationary wave called?

They are called progressive waves to differentiate them from stationary waves

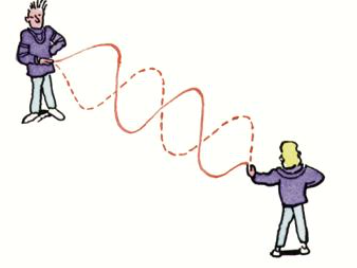
What do progressive waves combine to form at fixed points along the rope?

• Nodes points of zero/no displacement

At each node how many degrees out of phase are the two sets of progressive waves?

180° out of phase so they cancel each other out so there is zero displacement (node)

How would you determine where there are points of cancellation in the wavefronts from a ripple tank?

A gap in the wavefronts shows there has been cancellation (crest meets trough or vice versa)

How are points of reinforcement created in a ripple tank?

A trough created from a vibrating dipper meets a trough from another dipper or crest meets crest

What causes the effect known as interference?

• Waves are continuously passing through each other at constant frequency and constant phase difference

• Therefore cancellation and reinforcement occur at fixed positions

• The effect is known as interference

What do Coherent sources of waves do?

• They produce an interference pattern where they overlap

• This is because they vibrate at the same frequency with constant phase difference

What would happen if the phase difference of the progressive waves changed at random?

The points of cancellation and reinforcement would move about at random and no interference pattern would be seen

What can a microwave transmitter and receiver be used to demonstrate in waves?

• Reflection

• Refraction

• Diffraction

• Interference

• Polarisation

How would you show that microwaves become weaker as they travel away from the transmitter?

• Place the receiver in the path of the microwave transmitter

• Move it gradually away from the transmitter and note how the intensity drops as distance increases

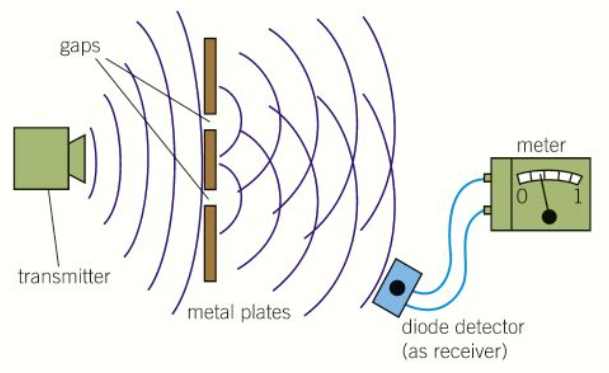
How would you show that microwaves cannot pass through metal?

• Place metal plates between the transmitter and receiver

• The reading on the receiver should be 0

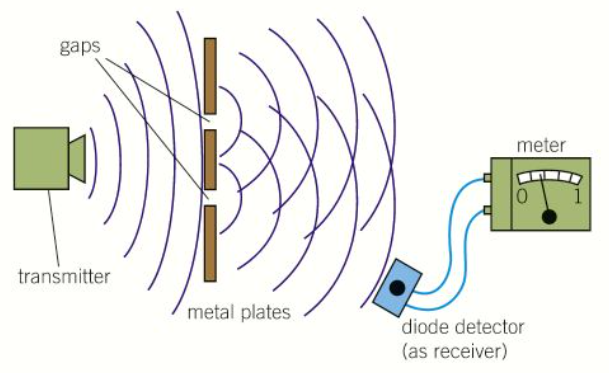
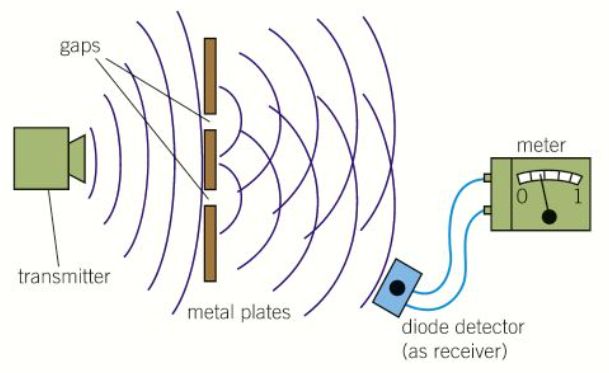
How would you show that microwaves diffract as they pass through a slit?

• Use two metal plates to make a narrow slit and show that the receiver detects microwaves that have been diffracted as they pass through the slit

• Show that if the slit is made wider, less diffraction occurs or vice versa

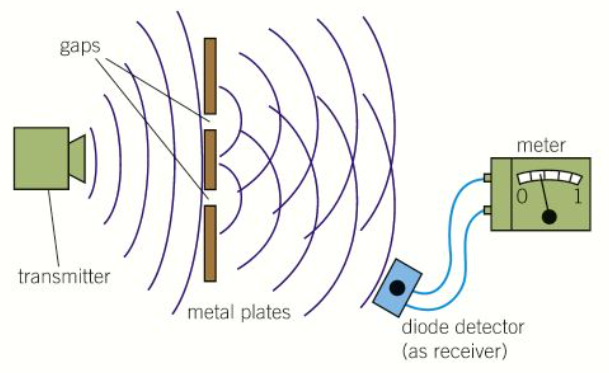
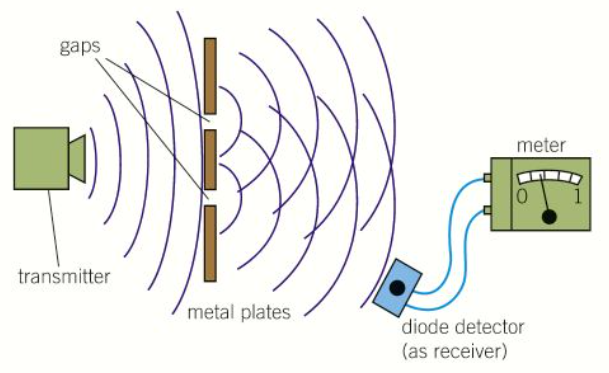
How would you show points of cancellation and reinforcement using microwaves?

• Use a narrow metal plate with two plates above to make a pair of slits

• Direct the transmitter at the slits and use the receiver to find points of cancellation and reinforcement where the microwaves from the two slits overlap

When are stationary waves formed?

When two progressive waves pass through each other

How can a stationary wave be formed on a string in tension?

• By fixing both ends and making the middle part vibrate,

• Progressive waves travel towards each end, reflect at the ends and then pass through each other

What is the simplest stationary wave pattern on a string called

The first harmonic (or the fundamental mode of vibration)

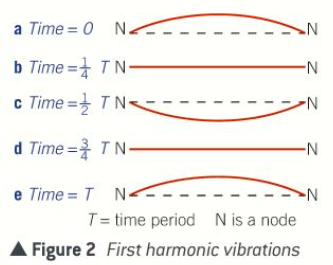
What does the first harmonic consist of?

• A single loop that has a point of zero displacement at each end (node)

• String vibrates with maximum amplitude between the nodes (antinode)

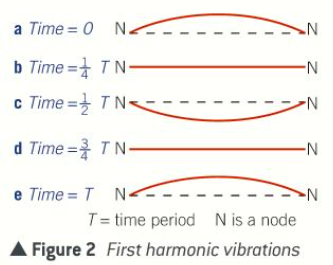
What is needed for the string to vibrate from side to side repeatedly in order to create the pattern of the first harmonic?

• Distance between nodes at either end (i.e. length of string) must be equal to one half-wavelength of the waves on the string

• Distance between adjacent nodes = 1/2λ

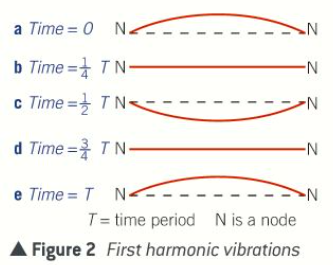
What happens if the frequency of the waves sent along the rope from either end is raised steadily from the first harmonic?

• The pattern from the first harmonic disappears and a new pattern is observed with two equal loops along the rope

• It has a node at the centre as well as either end

• It is formed when the frequency is twice as high as in figure 2, corresponding to half the previous wavelength

• Because distance between adjacent nodes = 1/2λ

• Length of the rope is one full wavelength

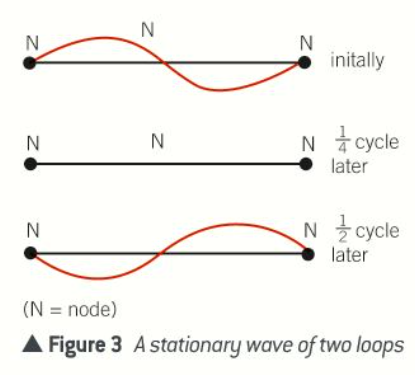
What is special about stationary waves that vibrate freely?

• They do not transfer any energy to their surroundings, unlike progressive waves

• This is because the amplitude of the vibration at their nodes is zero so there is no energy at the nodes

• Amplitude of vibration at the antinodes is at a maximum so there is maximum energy at the antinodes

• However, the nodes & antinodes are at fixed positions so no energy is transferred

When they are in phase, what do progressive waves do?

They reinforce each other to produce a larger wave

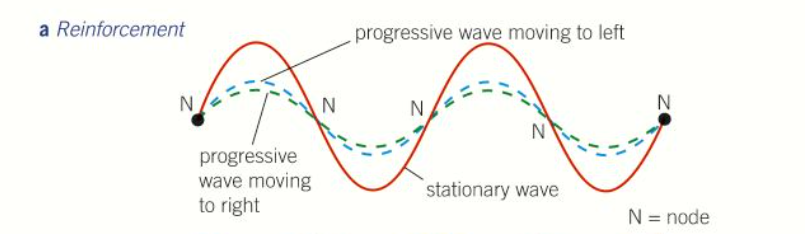
What happens to progressive waves ¼ of a cycle later after they were in phase?

• They have moved one quarter of a wavelength in opposite directions

• They are in antiphase so have cancelled each other out

What happens to the progressive waves ½ of a cycle later after they were in phase?

• They are back in phase

• The resultant is a large wave except in reverse direction

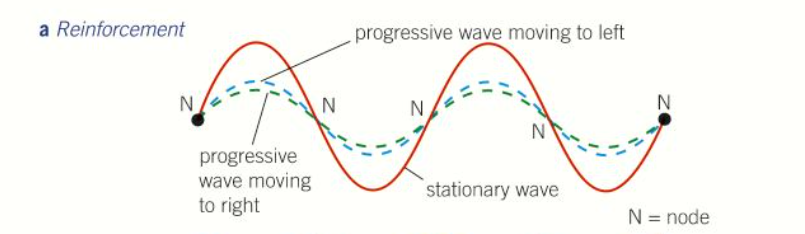
What happens at the nodes (point of zero displacement) that are fixed in position throughout

The stationary wave oscillates between the nodes. In general in any stationary wave pattern

How does the amplitude of a vibrating particle vary with position in a standing wave?

• zero amplitude at node

• maximum amplitude at antinode

How does the phase difference of vibrating particles vary between nodes?

• Zero if the particles are between adjacent nodes or separated by an even number of nodes

• 180° (2π radians) if the particles are separated by an odd number of nodes

How does frequency of particles vary between Stationary and Progressive waves?

• Stationary waves - All particles except those at nodes vibrate at the same frequency

• Progressive waves - All particles vibrate at the same frequency

How does the amplitude of particles vary between Stationary and Progressive waves?

• Stationary waves - Amplitude varies from zero at nodes to maximum at antinodes

• Progressive waves - Amplitude is the same for all particles

How does the phase difference between two particles vary between Stationary and Progressive waves?

• Stationary - equal to mπ where m is the number of nodes between the particles

• Progressive - equal to 2πd/λ where d = distance apart and λ is the wavelength

How is sound in a pipe an example of a stationary wave?

• Sound resonates at certain frequencies in an air-filled tube or pipe

• In a pipe closed at one end, these resonant frequencies occur when there is an antinode at the open end and a node at the other end

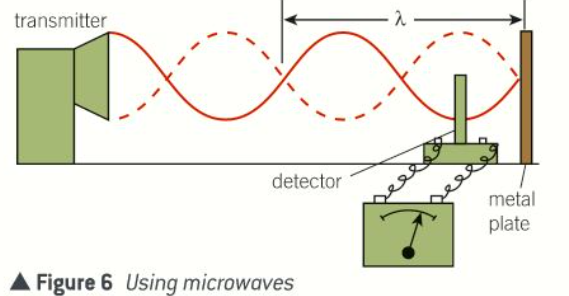
How can you use microwaves to demonstrate stationary waves?

• Microwaves from a transmitter are directed normally (90°) at a metal plate

• The plate reflects the microwaves back towards the transmitter

• When a detector is moved along the line between the transmitter and metal plate, the signal is found to be zero or minimum at equally spaced positions along the line

• The reflected waves and waves from the transmitter create a stationary wave pattern

• The positions where no signal (or minimum) is detected are where nodes occur

• Nodes are spaced at intervals of half a wavelength (λ)

Describe a controlled arrangement for producing stationary waves [PROCESS]

• String or wire tied at one end to a mechanical vibrator connected to a frequency generator

• The other end of the string passes over a pulley and supports a weight which keeps tension in the string constant

• As the frequency of the generator is increased from a very low value, different stationary wave patterns can be observed on the string

• In every case, the length of the string between the pulley and the vibrator has a node at either end

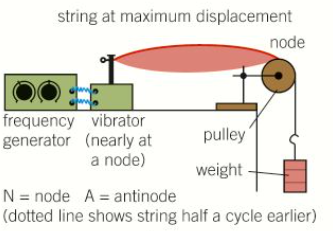
Where is the first harmonic pattern of vibration seen in the controlled arrangement for producing stationary waves?

• Seen at lowest possible frequency that gives a pattern

• Antinode in middle and node at each end

• Since length, L of the vibrating section of the string is between adjacent nodes and distance between them is ½λ₁

What is the wavelength of the waves that form the first harmonic pattern of vibration?

• λ₁ = 2L since distance between adjacent nodes is half a wavelength and Length of the string stays constant

• λ/2 = L so 2L = λ

What is the equation for the frequency of the first harmonic?

• f = c/λ₁= c/2L, where c is the speed of the progressive waves on the wire

• Also written as f₁ for the frequency of the fundamental mode of vibration

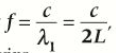
Describe the second harmonic stationary wave pattern

• There is a node in the middle so the string is in two loops

• The wavelength of the waves that form this pattern is λ₂ = L because each loop as a length of half a wavelength and there are two loops which, together, are equivalent to L

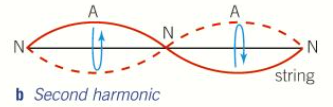
What’s the equation for the frequency of the 2nd Harmonic vibrations?

f₂ = c/λ₂ = c/L = 2f₁ (twice frequency of first harmonic)

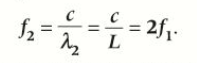
Describe the third harmonic stationary wave pattern

• Nodes are at a distance of 1/3L from either end and an antinode in the middle

• The wavelength of the waves that form this pattern is: λ₃ = 2/3L because each loop has length of half a wave-length and there are 3 loops

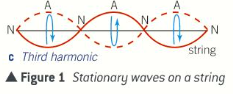
What is the equation to find frequency of the third harmonic?

f₃ = c/λ₃ = 3c/2L = 3f₁ (thrice the frequency of the fundamental mode of vibration)

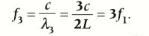
How do stationary wave patterns form on a vibrating string? [PROCESS]

• A progressive wave is sent out by the vibrator

• Crest reverses its phase when it reflects at the fixed end and travels back along the string as a trough

• When it reaches the vibrator, it reflects and reverses phase again so it travels away from the vibrator as a crest

• If this crest is reinforced by a crest made by the vibrator, the amplitude of the wave is increased

• This is how a stationary wave is produced

What is the key condition for a stationary wave to form?

The time taken for a wave to travel along the string and back should be equal to the time taken for a whole number of cycles of the vibrator

What’s the equation for the time taken for a wave to travel along the string and back?

t = 2L/c (where c is the speed of the waves on the string)

What’s the equation for the time taken for a vibrator to pass through a whole number of cycles?

t = m/f (where f is the frequency of the vibrator and m is a whole number)

How is the key condition for a stationary wave expressed?

• 2L/c = m/f (time taken for a wave to travel along a string and back is equal to the time taken for a vibrator to pass through a whole number of cycles)

• Rearranging gives formula f= mc/2L and λ = c/f = 2L/m

What frequencies are stationary waves formed at?

f, 2f, 3f etc.

What is the length of the vibrating section of the string which produces stationary waves?

L = mλ/2 (a whole number of half wavelengths)

What does a pitch of a note correspond to?

Its frequency

How can a pitch of a note from a stretched spring be altered?

• Changing the tension of the string

• Altering its length

How can a vibrating string or wire be tuned to the same pitch as a tuning fork?

• By changing length

• By altering tension

How is the sound from a vibrating string different than the sound from a tuning fork?

• Sound from a vibrating string includes all harmonic frequencies

• Tuning fork vibrates at a single frequency