2a - Atomic Structure

Early Attempts to Classify Elements

☆ Döbereiner’s Triads (1817): Groups of 3 elements with similar properties (e.g., Cl, Br, I).

☆ Newlands’ Law of Octaves (1865): Properties repeat every 8 elements when ordered by atomic mass.

☆ Mendeleev’s Periodic Table (1869): Arranged elements by atomic mass, predicted missing elements.

The modern periodic table

✧ Organized by atomic number (Z) rather than atomic mass.

✧ Elements in the same group have similar chemical properties.

✧ Elements in the same period show trends in physical and chemical properties.

Atomic structure

Nucleus:

✧ Protons

✧ Neutrons

Orbitals:

✧ Electrons

Atomic number v.s. mass number

✦ Atomic number (Z) = number of protons.

✦ Mass number (A) = protons + neutrons.

Bohr Model of the atom

• Electrons occupy quantized energy levels (n).

• Energy is absorbed when an electron moves to a higher level.

• Energy is released as a photon when an electron drops to a lower level.

Only works well for H, doesn’t explain multi-electron systems

Bohr formulas

✦ Energy of a photon emitted/absorbed: ∆E =|E_final - E_initial| = Rhc |1/ n²_final - 1/n²_initial|

✦ Using De Broglie (E=hv) and c=λv: 1/λ = R |1/ n²_final - 1/n²_initial|

✦ Radius and energy of a certain orbital

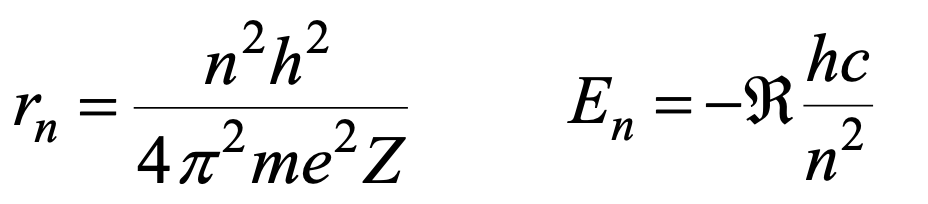
Wavelengths of particles

Using De Broglie’s equation:

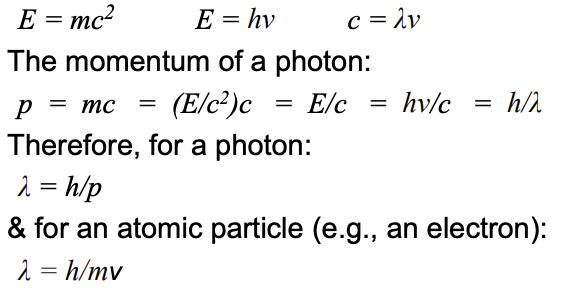
(c = speed of light @ 2.998 x 10⁸ m/s; p = particle momentum; h = Plank’s cte)

Wave mechanics

Electrons behave as standing waves fixed on the nucleus, not particles in circular orbits.

Wave-function Ψ= sin(nπx/l) describes the probability distribution of finding an electron (length of sine wave limited to ½, 1,…, n/2 wavelengths)

Node

Position/lines/planes/surfaces where the wave’s function has a zero value.

They are found where the mathematical sign of the function changes (inflection point)

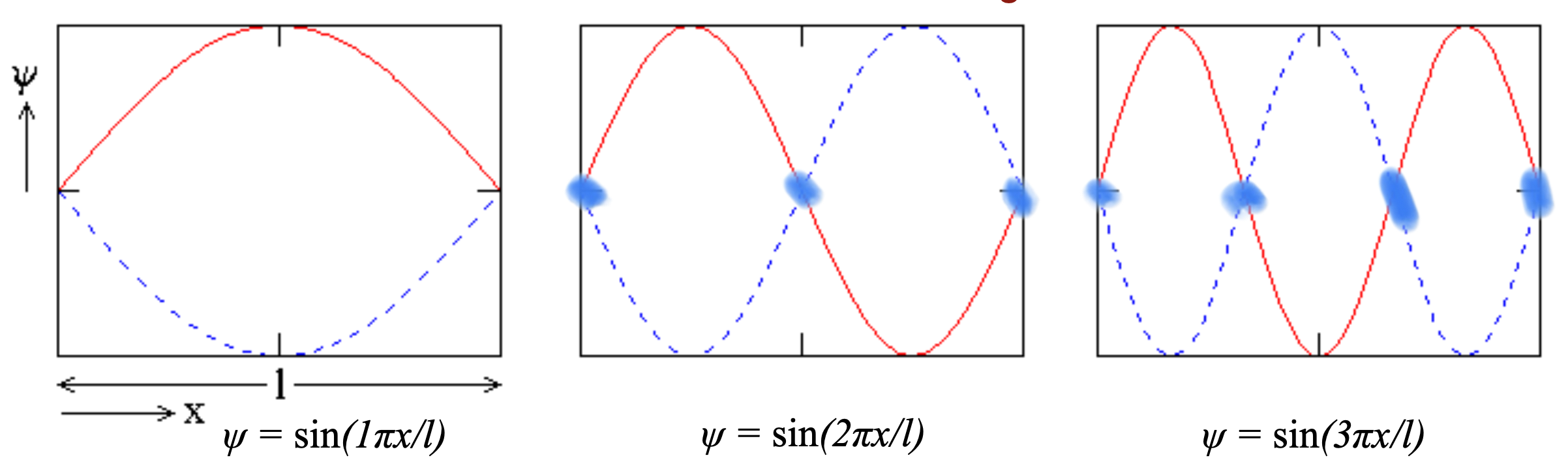
How can you find the number of nodes?

Using quantum numbers.

For planar nodes, this is determined by l (l=0, s; l=1, p;..). A p orbital electron has 1 planar node

For spherical/radial nodes, the formula n-l-1.

i.e. if n=3, l=1 there is 3-1-1 = 1 spherical node and 1 planar node

Orbitals

Regions of high probability of finding an electron.

✧ 𝛹² is proportional to the probability of finding an electron at a given point in space

The Schrödinger Equation

Allows us to describe the wave properties of an electron in terms of position, mass, total energy, potential energy: HΨ = EΨ

What does potential energy result from?

V results from electrostatic attraction between the electron and the nucleus (2 electrons simultaneously attracted by their respective nuclei whilst repulsing each other)

Described in the 2nd part of the Hamiltonian Operator

✦ Attractive forces = - potential energy

✦ An electron close to the nucleus has a large -V.

✦ Electron @ infinite distance: V=0

Quantum numbers

• Principal quantum number (n): Energy level, n = 1, 2, 3, ...

• Angular momentum quantum number (ℓ): Orbital shape (s, p, d, f), n-1,…, 0

• Magnetic quantum number (m_ℓ): Orientation of orbital, from -ℓ to +ℓ

• Spin quantum number (m_s): Electron spin (+½, −½).

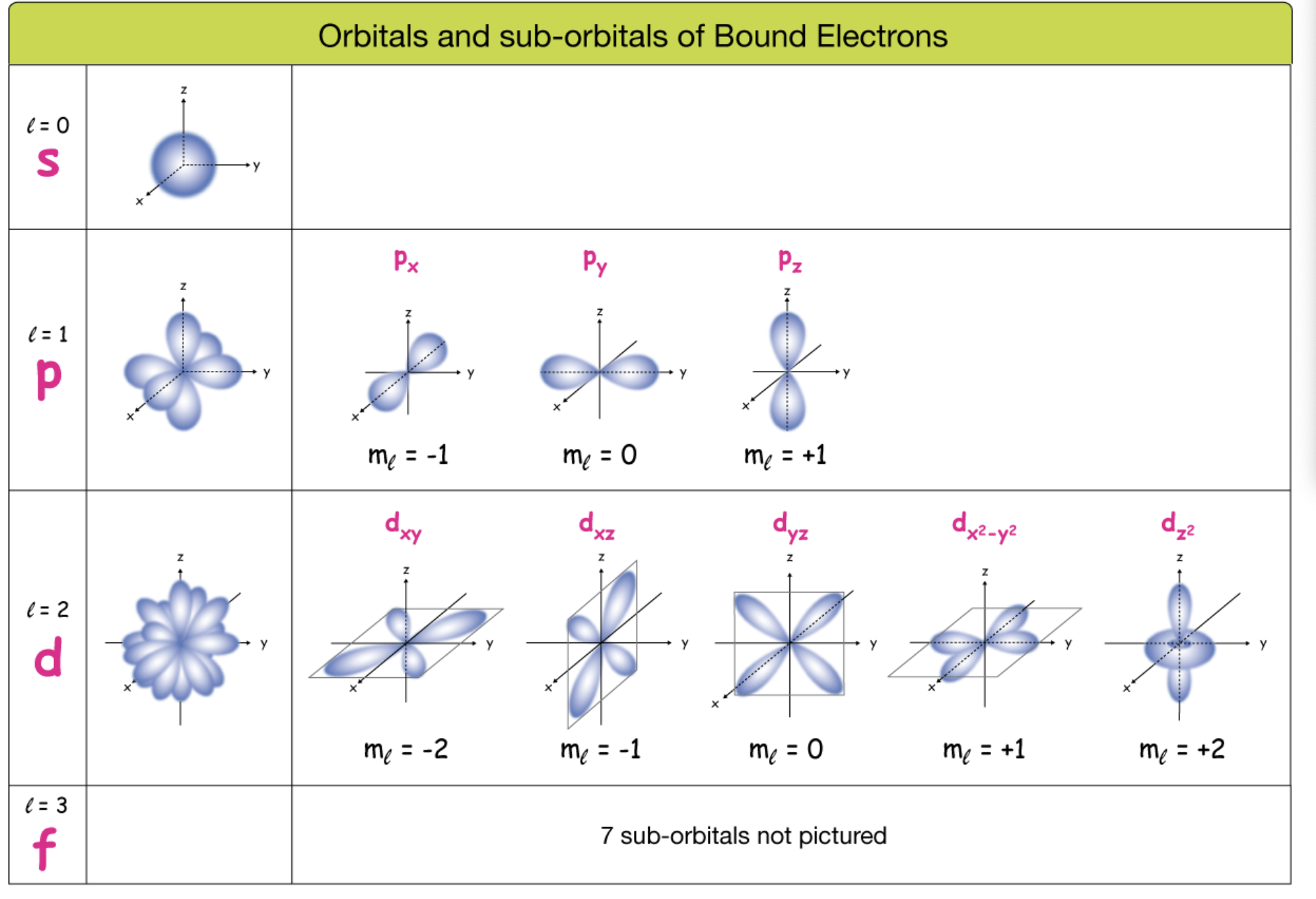
Atomic orbitals & their shapes

• s-orbitals: Spherical.

• p-orbitals: Dumbbell-shaped.

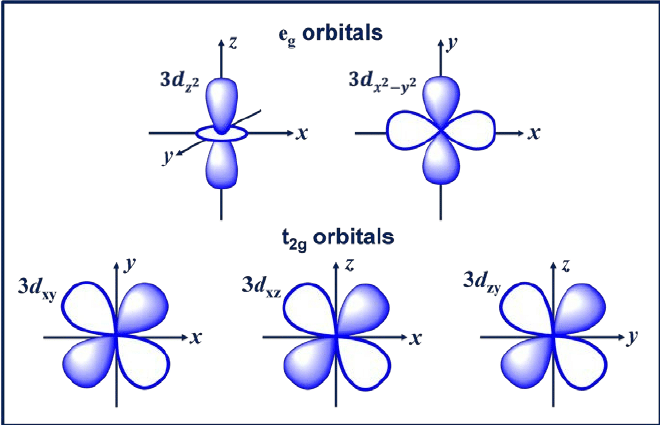
• d-orbitals: Cloverleaf-shaped (except dz², toroidal).

• f-orbitals: Complex multi-lobed shapes.

Allowed energy formula

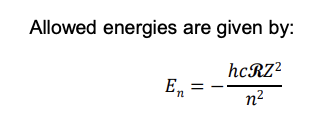
More negative E_n value → e⁻ is closer to nucleus

Electron configuration rules

✧ Electrons fill lower energy levels first (1s, 2s, 2p, 3s, 3p, etc.).

✧ Hund’s Rule: Electrons fill degenerate orbitals singly before pairing.

✧ Pauli Exclusion Principle: No two electrons can have the same set of quantum numbers.

✧ Afbau Principle: lower energy orbitals must be filled first

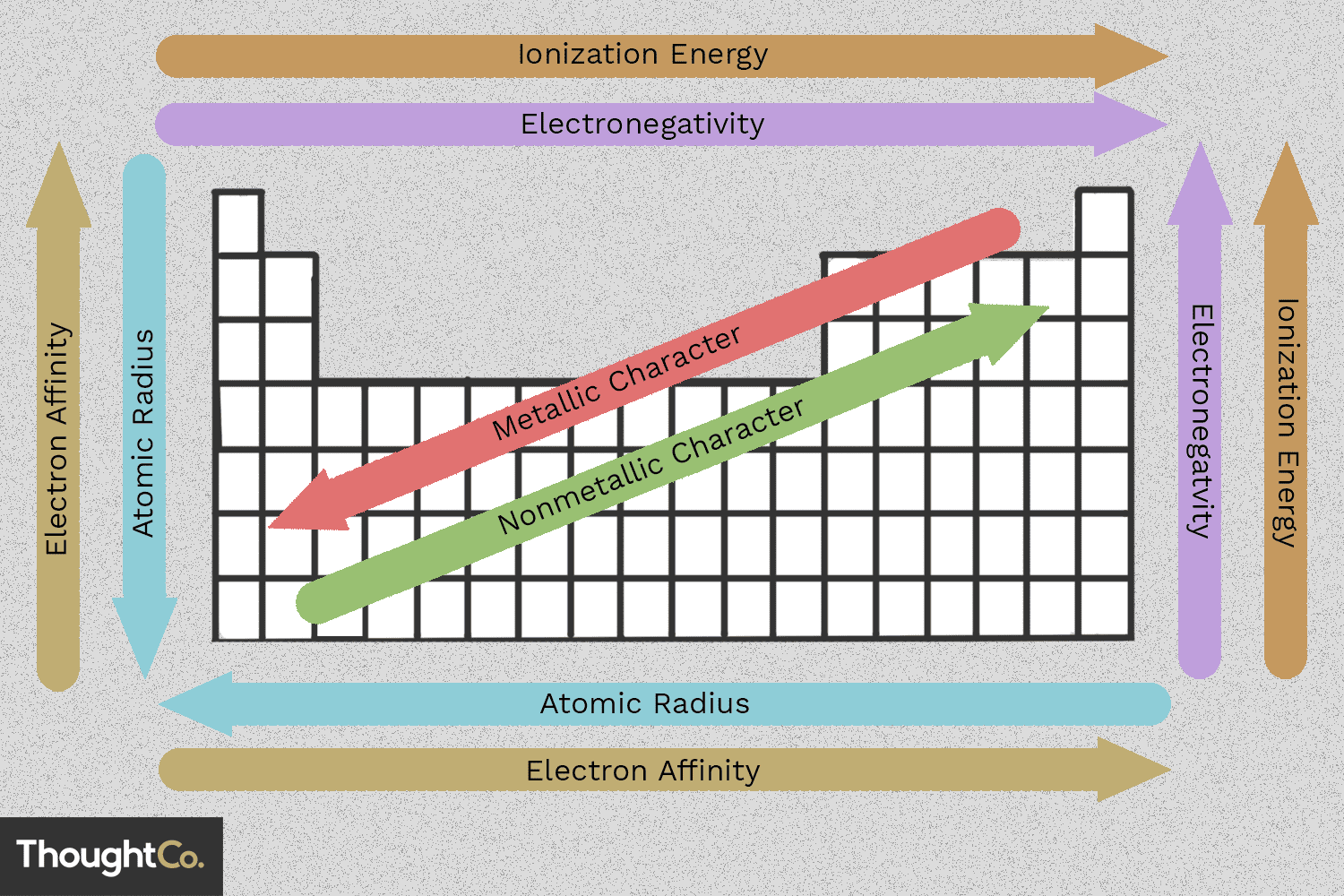
Periodic trends

✦ Atomic Radius: Decreases across a period, increases down a group (more shells).

✦ Ionization Energy: Increases across a period, decreases down a group (easier to remove an electron).

✦ Electron Affinity: Becomes more negative across a period (stronger attraction for electrons).

✦ Electronegativity: Increases across a period, decreases down a group.

Heisenberg Uncertainty Principle

✧ Cannot precisely know both position and momentum of an electron.

✧ The more accurately an electron’s energy is known, the less accurately its position is known.

✦ ∆x. ∆p > h/4π where ∆x is the uncertainty in position and ∆p the uncertainty in momentum

Radial probability density

The likelihood of finding an electron at a given distance from the nucleus.

The points where the probability of finding an electron is zero are radial nodes

Electron probability

• s-Orbitals: Have a high probability near the nucleus but decrease with distance.

• p, d, f Orbitals: Show more complex radial distributions, with multiple nodes.

Radial Distribution Function (RDF)

Gives a measure of the probability of finding the electron at a specific distance from the nucleus, i.e., somewhere in a thin sphere of specified radius

3d orbital shapes

✧ 4/5 3d orbitals have 2 transverse planar nodes and no radial nodes

✧ the 3d_z² orbital has a conical node