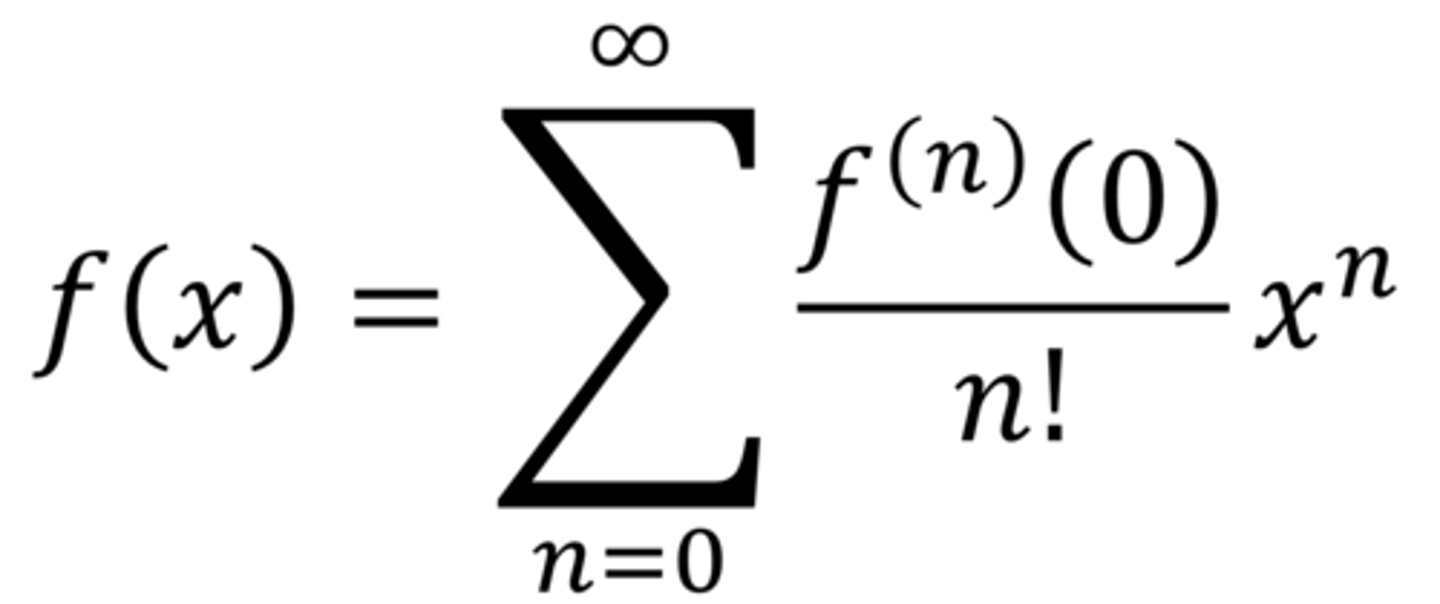Pitt Calculus 2 - Series

Geometric series

*convergent when |r| < 1

*divergent when |r| ≥ 1

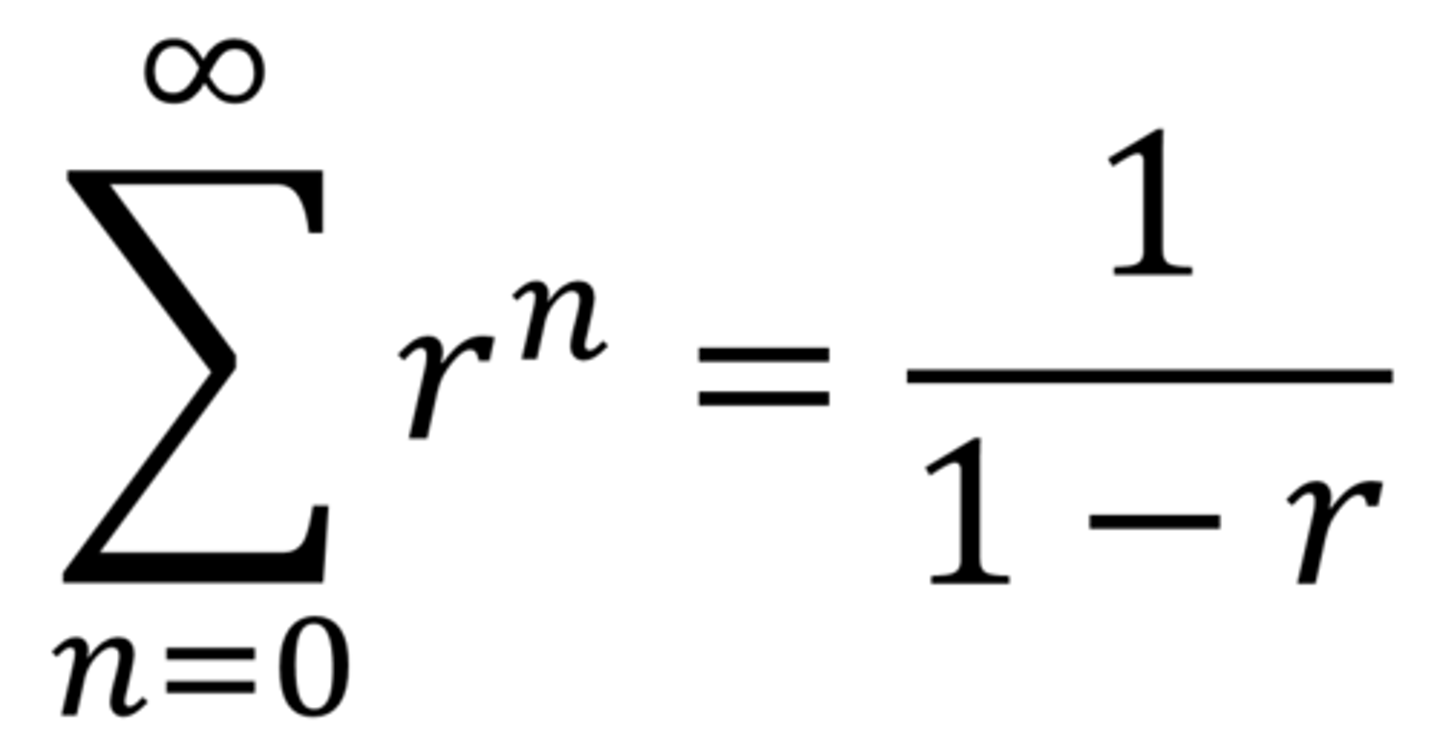
P-series

*convergent when p > 1

*divergent when p ≤ 1

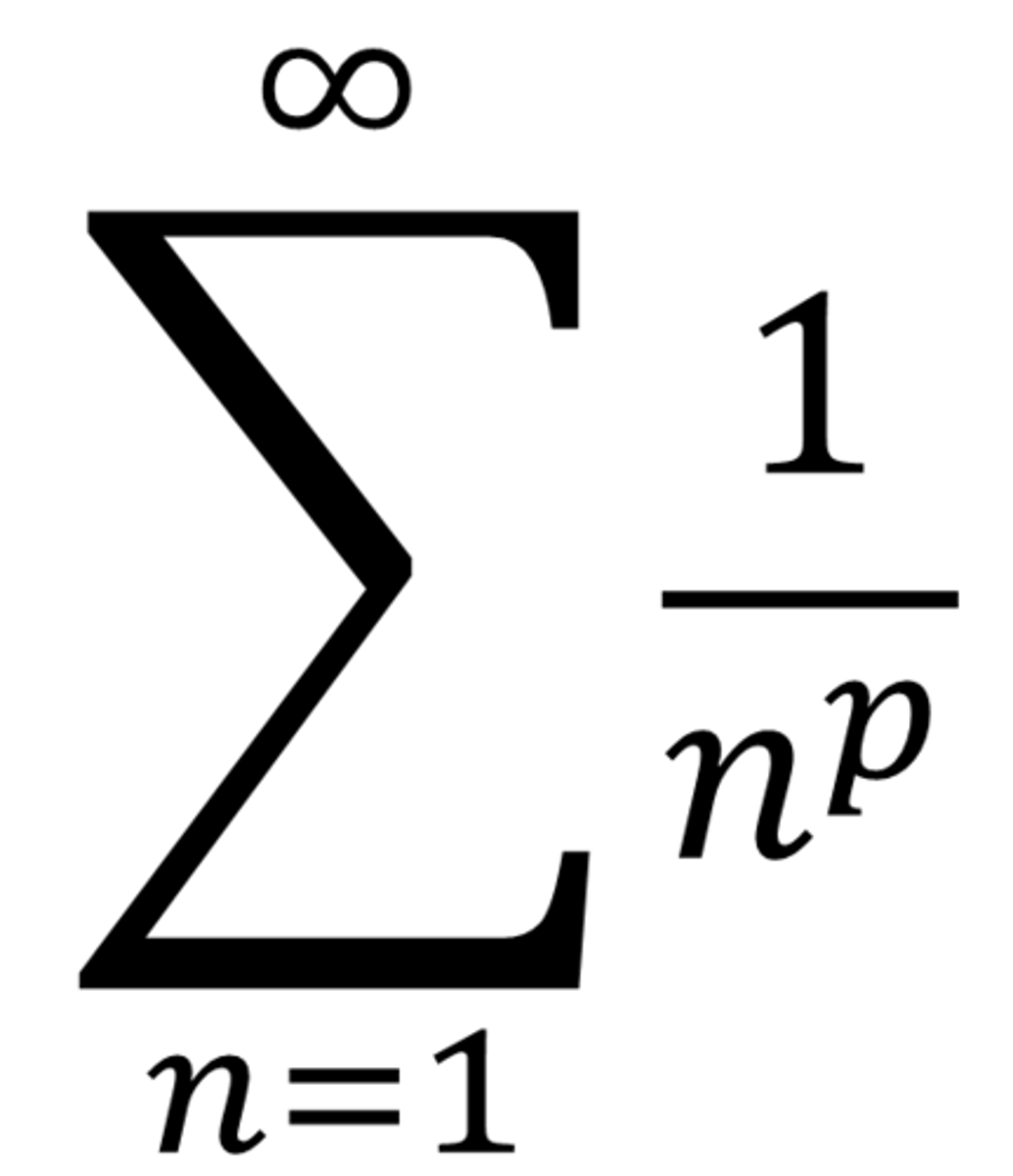
Limit theorem

If the infinite series Σa_n is convergent, then lim_n→∞ a_n = 0

If lim_n→∞ a_n ≠ 0 or DNE, then the infinite series is divergent

Integral test

*F must be continuous, positive, and decreasing on [1,∞)

Let a_n = f(n)

The infinite series Σa_n is convergent iff if the improper integral ⌡1 to ∞ f(x)dx is convergent

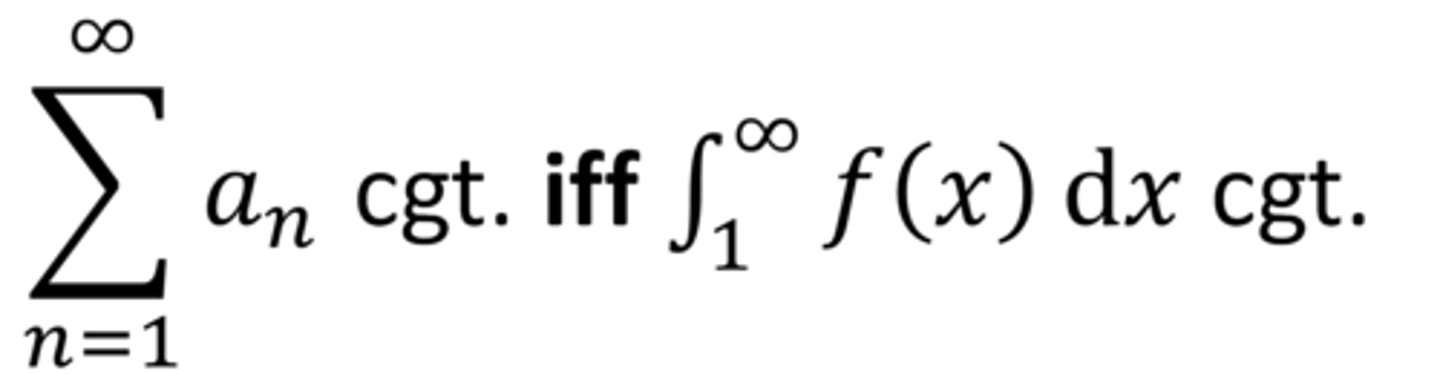
Comparison test

*Σa_n and Σb_n are series with positive terms

If Σb_n is convergent and a_n ≤ b_n for all n, then Σa_n is also convergent

If Σb_n is divergent and a_n ≥ b_n for all n, then Σa_n is also divergent

Limit comparison test

*Σa_n and Σb_n are series with positive terms

If If lim_n→∞ (a_n/b_n) = c, where c is a finite number and c>0, then either BOTH series converge or diverge

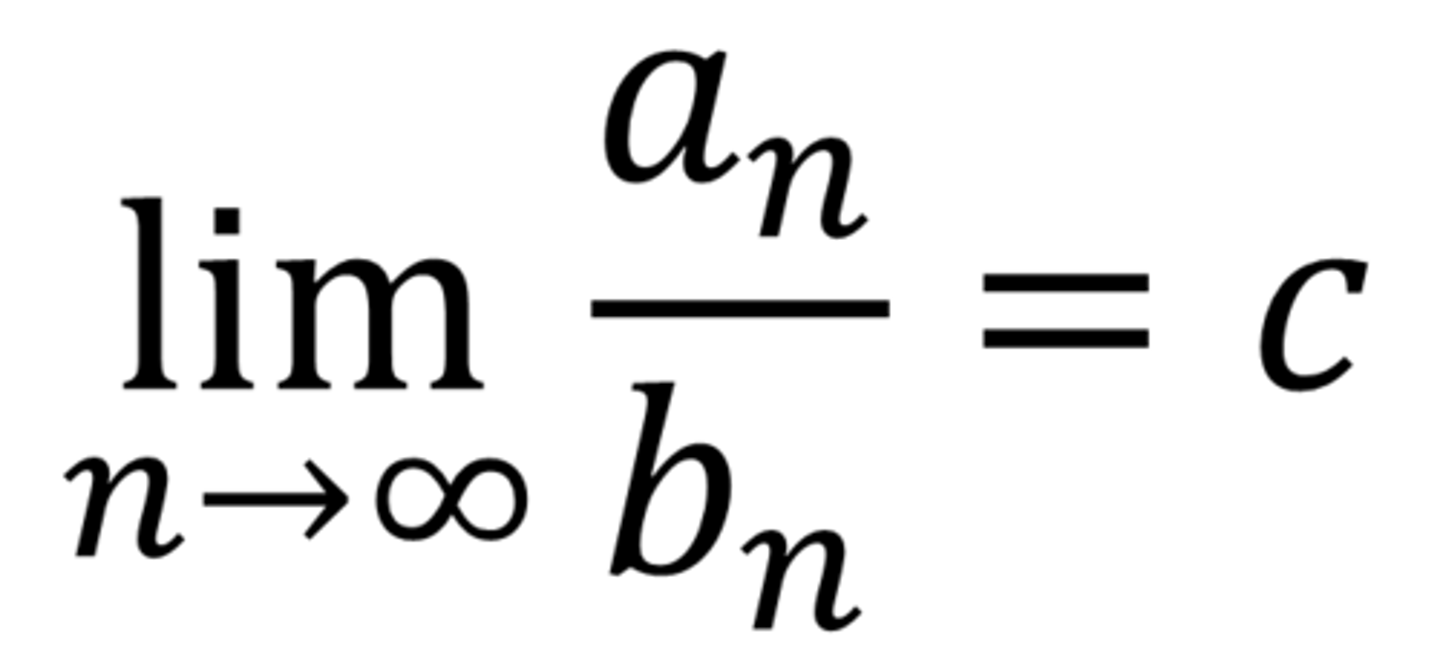
Alternating series test

Ratio Test

Root test

Taylor series general form

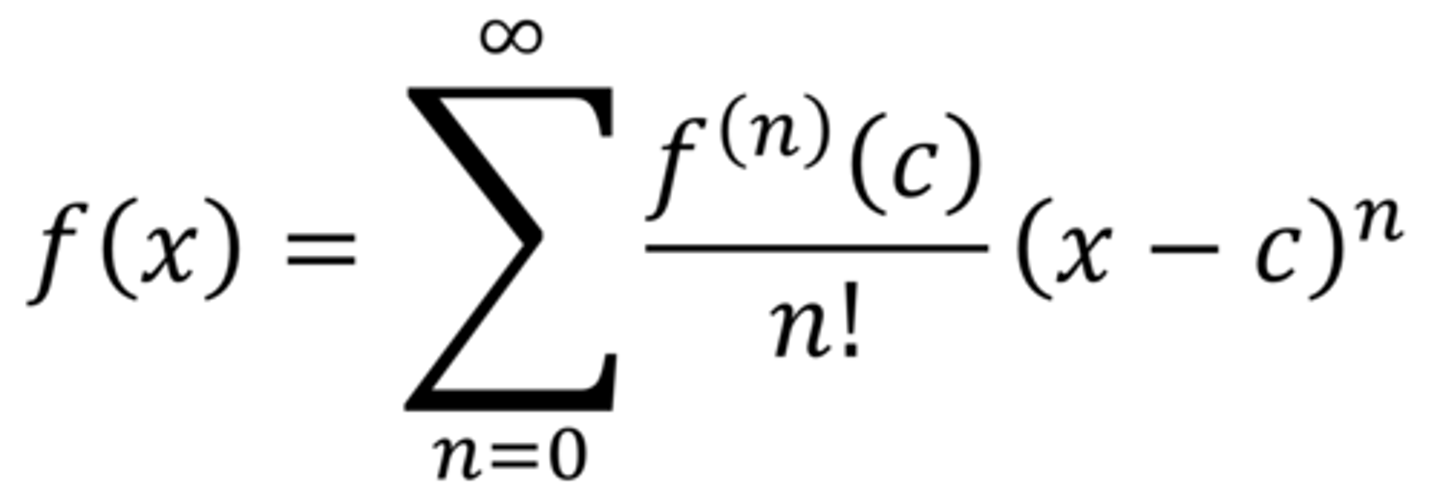
Maclaurin series general form