CS141

Takes a function that has pair as input and single value as output, and converts it to a function that takes two parameters and produces a single output.

Implemented as shown in the picture

How does curry work, and how do you implement it?

Takes a function that takes two parameters as input and single value as output, and converts it to a function that takes a pair as input and produces single output

How does uncurry work, and how do you implement it?

Takes a function as its first argument (representing some operation), a starting value, or accumulator as the second argument, and then list of values.

Foldr is a combination of the binary operations for all the values, with the accumulator at the end.

How does foldr work?

How to implement foldr from scratch?

This means we evaluate things to the left of the function first. Functions in Haskell by default are left-associative.

What does left-associative mean?

infix[l/r] → left or right associative

[precedence] → between 0 to 9

operator - value of operator

What is fixity declaration, and how is it used for operators? How can we then define operators?

foldr is right associative, meaning we unfold our expression towards the right

foldl is left associative, meaning we unfold our expression towards the left

Difference between foldl and foldr?

Function application operator. Equivalent to (). Right associative.

Purpose of $?

Function composition operator. Right associative.

g . f = g (f(x))

Purpose of .?

This is the number of values a data type has.

What is the cardinality of a data type?

Type that has one or more constructors. Find cardinality by adding cardinalities of its input types.

What is a sum type? How do we calculate its cardinality?

This is a type that is parameterized by some values. Find out cardinality by getting product of cardinalities of its parameter types.

What is a product type? How do we calculate its cardinality?

Pair (a, b). Determine it by multiplying cardinality of a by b.

What is the classic polymorphic product type? And how do we determine its cardinality?

Either a b. Determine by adding cardinality of a and b

Classic polymorphic sum type? And how do we determine its cardinality?

We can use newtype when dealing with wrapper types (data type with one constructor, and the constructor has only one parameter). It tells compiler to treat the given data type as the type of the parameter, being slightly more optimised than using data.

Can also allow you to have multiple instances for a given type. For example, show already has instance for string. If we wanted to have our own implementation, can use newtype as shown in the picture:

When can we use newtype, what is it, and what benefits does it provide?

Allows us to provide an alias, particularly useful for longer types.

Purpose of type keyword?

Type class used to abstract over things that can be folded over. Allows us to use folding functions on the type, such as foldr.

Can make an abstract class foldable using the syntax provided in the diagram

Purpose of Foldable? How to make an ADT Foldable?

Type class used to abstract over data types that can be mapped over, using fmap.

Can make an ADT a functor using the syntax provided in the diagram.

Purpose of Functor? How to make an ADT a Functor?

Functors must b structure preserving - outputs need to be same shape as inpiut - only underlying values can change

Functors must obey the identity law: fmap id x === x

fmap distributes over function composition: fmap (f.g) x === (fmap f . fmap g) x

What are the three functor laws?

How to implement functor for maybe type?

*

What is the kind of a type taking zero parameters, like Bool or String?

For maybe: * → *

What is the kind of a type constructor, like Maybe, and why?

Use unconstrained type variables to write function which are fully generic with respect to values they operate over.

What is parametric polymorphism?

Writing functions constrained by type classes and make use of type class interface when defining the function.

What is ad-hoc polymorphism?

Used to enforce that every instance of a type class is already an instance of some other type class, making the precondition a global requirement.

What is subtype polymorphism?

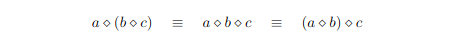
This is an algebraic structure admitting notion of combining two values with a binary operation. Represented using <>. Associative as seen in the diagram.

What is a semigroup? How is represented in Haskell?

This is a semigroup equipped with an identity, also known as mempty. As such, typeclass for monoid is subtyped by semigroup.

What is a monoid?

Value does not change when combined with identity, either to the left or the right

Identity laws for mempty?

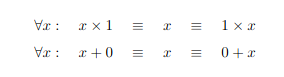
Because there are two semigroups for numbers, as indicated in the picture on the side.

Can import from Data.Monoid. Use Sum and Product.

Why can’t we directly define semigroup for numbers? What can we use instead?

Takes as first param number of times to repeat, second param the semigroup value, uses the semigroup to combine the semigroup value the provided number of times.

Purpose of stimes?

Takes list of monoidal values, combines them together

Purpose of mconcat?

Every type that can contain values.

What is an inhabited type?

Functions are values representing computations. They can be manipulated to form new computations.

What are functions in the context of Haskell?

*, as functions are inhabited types and thus are values.

Kind of a function?

c* → c* → *

This is because →

takes two types of kind * ( a and b)

and produces a new type

a → b, which we know has a type of c* as type of a function is c*.

Type of →? And why?

← As shown in the picture

Since we are combining outputs of both functions together to form the output of the semigroup operation, the outputs of both functions (b) need to be semigroups as well.

How can we implement functions as semigroups, and how does this work?

← As shown in the picture

Need to ensure b is Monoid for Monoid instance, as this provides us a mempty value that we can use.

How to implement functions as monoids, and how does this work?

← As shown in the picture

Functor instance for (->) e means: mapping a function f over another function g means composing f and g.

fmap = (.) is elegant because it’s just function composition.

This idea treats functions as “containers” of values indexed by e.

It’s foundational for thinking about computations in functional programmin

How to implement functions as functors?

Lifted - when a value lives inside a functor

Unlifted - value that does not live inside a functor

E.g Maybe Int → Value of type int has been lifted into Maybe (Which is a functor)

fmap thus takes a function and applies it to a lifted value to give a new lifted value.

What does lifted and unlifted mean? How can we thus define fmap?

Stores zero or more pieces of data, that can be manipulated by mapping over the data, or retrieving using functions like toList.

What is a data functor?

Used to dictate ways in which data can flow through code.

What is a control functor?

This is a function used to apply a lifted function into a lifted value.

How does <*> work for Applicative Functors?

Applying lifted identity id to lifted value shouldn’t change the value

Function application in functor faithful to function application outside functor

Applying lift function still faithful when we swap the arguments.

Laws for an applicative functor?

Apply to Just 5, giving JUst 5, partially applied function. then apply partially applied lifted function to JUst 6, giving JUst 30

How does this work?

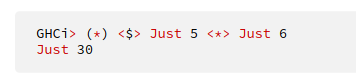
Used to lift a value into an applicative context.

e.g pure (+3) <*> Just 4

pure (+3) in this context leads to 3 being lifted as Just 3.

Just 3 <*> Just 4 → Just <7>

Purpose of pure?

Apply a list of functions to a list?

This is used when we want to pass a lifted value into a function that returns a lifted value.

What is the meaning of »= and write a monad instance for maybe

Working with values inside a monadic data type. Each data typ with monad instance has its own meaning for the computational context.

What is a computational context?

Lifting a value and then binding it through a function should give the

same output as just running it through the function directly.

Binding a value through pure should be the same as doing nothing.

Binding through f then through g should give the same result regardless of which order the binds are applied in

What are the three monad laws?

Applicative is subclass of Functor

Monad is a subclass of applicative (and by extension Functor)

Relationship between Functor, Applicative and Monad?

COmputations which can fail instead of returning a value.

COmputational context for maybe?

All possible outcomes of computation

COmputatial context for []?

COmputatios with failure values and happy path

COmputational context for Either?

COmputations that share an environment, e.g an input parameter.

COmputation context for ((→) e)

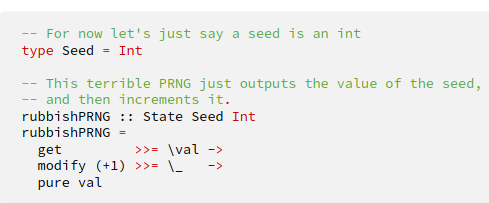
State datatype stores a function, returning a tuple containing a value, and another value of type s. Passing the value through and modifying it is s being a stateful parameter which can be interacted with.

How does State work?

Retrieves and returns value of state.

Purpose of get?

Takes a replacement value, sets state to that.

Purpose of put?

Applies a modification function to a stateful component, can be defined using get and put.

Purpose of modify?

• gets the value from the stateful component and passes it through as an argument

called val;

• modifies the stateful component to increase it by 1;

• returns the value of the stateful component by lifting it into State

Explain what is going on here:

This is the unit type.

Purpose of () type?

This is a computation that exists in the IO monad, and can make interactions with the real world (e.g getting line from standard input, writing line of text to standard output), and returns unit ().

What is the meaning of IO ()?

COmputations that can interact with some additional stateful component which is threaded through functions.

Computation context for state?

Word do followed by series of expressions, one per line. Each is sequenced automatically with »=.

What is a do block?

It means that I/O doesnt have a meaningful runtime representation w can work with. No way to unpack the real world we thread and modify, so there is no way to work with it outside primitive operations and control flow combinators

There is no way to escape I/O - no function to go from value of type IO to value of typ a.

What does it mean that I/O is opaque?

Do notation is useful when we want to run a lot of operations relying on a monadic effect such as State or IO.

When do we not use do notation?