Kin 483-Ch.11: Factorial Analysis of Variance

Review

• Chapter 9 (ANOVA): the effect of different exercise programs

  • IV

  • Levels:

• Chapter 10 (ANOVA RM): the effects of riding a stationary bike on fatigue at various time intervals over a 60-minute period

Each of these has one independent variable!

Identify the Independent and Dependent Variable(s) in the following scenario:

What is the effect of 3 different protein amounts, consumed post workout, on body composition in both men and women?

• Dependent: body composition

• Independent:

  • Amount of protein (3 levels)

  • Gender (2 levels; female/male)

Factorial Analysis of Variance: 3 × 2 ANOVA

Scenario: What is the effect of differing protein amounts, consumed post workout, on body composition in both men and women?

• Analyzes differences of the dependent variable (body composition) on 2 factors - protein (different amounts) & gender (male and female)

• This is called a 3 x 2 ANOVA

  • (protein x gender)

  • 3 levels of protein, 2 levels of gender

Factorial Analysis of Variance: 3 × 2 × 3 ANOVA

Scenario: What is the effect of differing protein amounts, consumed post workout, on body composition in both men and women?

• What would it be if we added 3 age groups?

  • 3x2x3 ANOVA

  • (protein x gender x age group)

• How can we make this a repeated measures design?

  • -not gender

  • -longitudinal study

F-Values and P-Values

• Just like the previous ANOVA’s we studied, Factorial ANOVA’s also produce F-values and p-values.

• We get an F-value for each factor (using our previous example)

  • We get an F-value for: Protein, Gender, Age

  • We also get an F-value for the interaction of factors

Interaction

• the combined effect of the factors on the dependent variable

  • Example: give both men and women protein

    • Protein strongly affects men but not women

    • significant interaction

  • Example: give both men and women protein

    • protein affects both men and women in the same way

    • nonsignificant interaction

Analysis

When you get your results you will look for 3 things in the following order:

1. Main Effects

2. Interaction

If you have no main effects or interaction the analysis stops here

3. Simple Effects for each factor

4. Post Hoc comparisons (if 3 or more IVs)

SPSS: 2×2 Factorial Example

1. Import Data (specify you only want to put in 2×2 data)

2. Variable View (make sure variables are classified correctly)

3. Analyze —> General Linear Model —> Univariate

4. Dependent Variable (ROM) ; Independent Variables (Stretching, Sex)

5. Options —> Descriptive Statistics—> Continue

6. EM Means* —> Display Means for : (Independent variables : stretching, sex) —> Compare Main Effects —> Adjustment: LSD —> Continue

*For 2×2, you need to do EM means instead of Post Hoc because SPSS won’t do post Hocs

SPSS: 2×2 Factorial Analysis

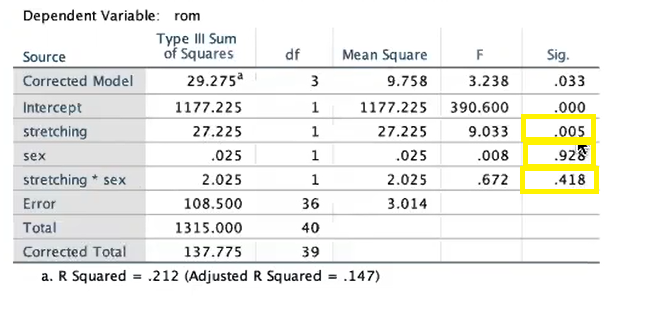
Tests of Between-Subjects Effects

• Check significance of independent variables

  • stretching (0.05)

  • sex (0.928)

  • stretching * sex (0.418)

    • If none are significant—> accept null hypothesis

Pairwise Comparisons

• Sex: no significance

• Stretching: Significance between stretching 1 and stretching 2

  • find out where differences are

Estimates

• Check mean value; which has greater ROM ?

  • stretching 2 (6.250 vs. 4.600)

• Make conclusionary statements

SPSS: 3×3 Factorial ANOVA Example

1. Import Data (specify you only want to put in 3×3 data)

2. Variable View (make sure variables are classified correctly)

3. Analyze —> General Linear Model —> Univariate

4. Dependent Variable ; Independent Variables

5. Options —> Descriptive Statistics—> Continue

6. Post Hoc —>Factors (stretching, age group); Post Hoc Tests for (stretching, age group) —> Tukey —> Continue

SPSS: 3×3 Factorial ANOVA Analysis

Tests of Between-Subjects Effects

• Check significance of independent variables

  • If none are significant—> accept null hypothesis

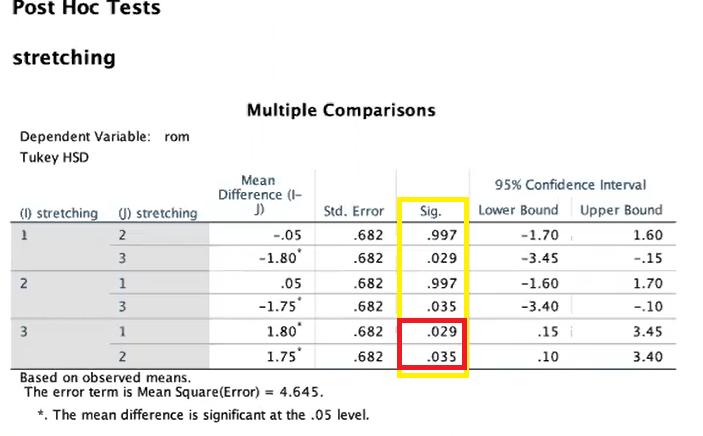
Post Hoc Tests: Multiple Comparisons

• Only look if one of IV is significant OR if the interaction between them is significant

  • do NOT look at post hocs if IVs are significant AND the interactions

• Difference between 3 and 1 and 3 and 2

Estimates

• Check mean value; which has greater ROM ?

• Make conclusionary statements