L02 - Basics of Modeling and Evaluation

1. Modeling techniques 2. Linear Regression 3. Choosing the right model 4. K-Nearest-Neighbor Classification 5. Model evaluation

What are the categories of Machine Learning?

1. Supervised Learning: Training data includes desired outputs

2. Unsupervised Learning: Training data does not include desired outputs

3. Reinforcement Learning: Reward from sequence of actions

Supervised Learning

Typical data structure types

A feature (attribute) is a data item that represents a characteristic or a property of a data entity.

The label is the desired output of the machine learning algorithm, e.g. the attribute that we want to predict

What is the given and goal for the supervised learning?

Given: examples of input data(features) X and output(label) Y

Goal: predict function Y=F(X) for new, unknown examples X

Supervised Learning

Regression and Classification

• If the target F(X) is continuous, the task is called Regression.

  • Sayılarla ifade edilen, ölçülebilen, kesintisiz değerler.

• If the target F(X) is discrete, the task is called Classification.

  • Sayılı, sınırlı ve genellikle kategori şeklinde veriler.

How do machine learning algorithms work?

Every machine learning algorithm has three components:

• Representation

  • Choosing the modeling type and thus defining the space of allowed models

• Evaluation

  • Scoring function or cost-function to judge the models and distinguish good models from bad models

• Optimization

  • Process of finding the best model in hypothesis space based on the given scoring function

Linear regression
Representation

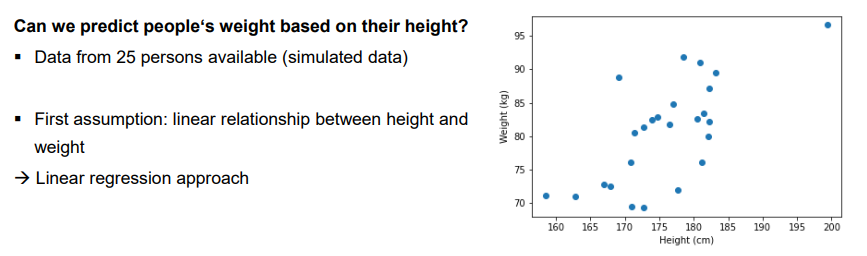
• Linear regression is one of the simplest machine learning models

Linear regression
Evaluation

• The linear models need to be evaluated using a scoring function

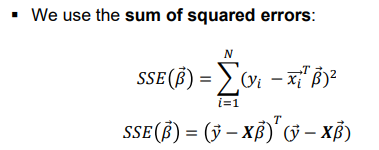
Linear Regression

Optimization

• To find the optimal parameters \overrightarrow{\beta}, the SSE needs to be minimized

• To find the minimum of the SSE, the derivative is set to 0 and solving for \overrightarrow{\beta}

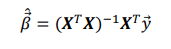
What if there is no analytical solution?
Different definition of optimization?

Optimization in machine learning means finding the minimum of a cost function. In most cases, iterative approaches have to be implemented to find the minimum.

Gerçekte, bu minimum değeri tek adımda bulmak çok zor.

Terim	Basit Anlamı
Optimization	En iyi çözümü bulma
Cost Function	Modelin hata miktarını ölçer
Iterative Approach	Deneye deneye daha iyi sonuç bulma

Gradient descent

A simple optimization algorithm steps

1. Choose a starting point x

2. Calculate the gradient ∇𝑓(𝑥) of the cost function at the starting point

3. Step in the direction of the negative gradient (steepest descent)

   • x^{^{\prime}}=x-\gamma\nabla f\left(x\right)

4. New iteration

What are the hyperparameters?

In machine learning, hyperparameters \gamma are parameters that control the learning process. They are not part of the resulting model.

The learning rate \gamma is a hyperparameter and defines the size of the iteration steps.

What is a good model?

1. Has a low error

   Predictions should be close to the actual values.

2. Generalizes well to unknown data

   Model predictions should work just as well for new, unknown data points.

The error is made up by three terms

Bias

• The bias of an estimator for a random variable y is the difference between an estimator expected value and the true value of the parameter being estimated.

• The bias is independent of the training set considered and 0 for a perfect learner

• It can be thought of as a systematic error due to incorrect assumptions in the model.

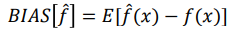
Variance

The variance of an estimator measures how much the estimator spreads out from its average value.

The variance is independent of the true value y and 0 for a learner that always predicts the same for all training sets.

It denotes changes in the model when using different training data

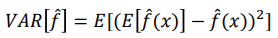
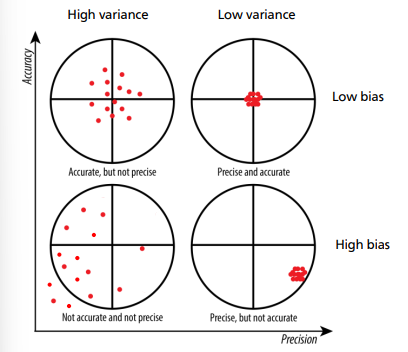
Accuracy, precision

Draw the diagram also

Accuracy assesses how close the results are to the actual value (bias of the results).

Precision assesses how close the results are with each other(variance) and therefore, how well the output is reproducible.

Bias-Variance-Trade-off

Goal: minimze both bias and variance

Very often, reducing variance leads to a higher bias and vice versa

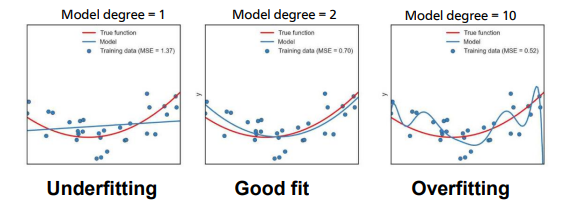
Overfitting and Underfitting

Underfitting: A model that suffers from underfitting is too general for a problem solution so that it is no even able to repeat the data it was trained with. The model has high bias and low variance.

Overfitting: A model that suffers from overfitting is too much adjusted to its training data so that it is not able to generalize the problem but repeat exactly what it has learned. The model has low bias and high variance.

	Underfitting	Overfitting
Model	Too general	Too specific
Problem	Can't learn training data	Learns only training data
Generalize?	Already bad on training	Can't generalize to new data
Bias	High	Low
Variance	Low	High

How to improve a model?

General recommendations for underfitting and overfitting models?

Underfitting model	Overfitting model
Increase model complexity (helps to reduce bias)	Add more training data (helps to reduce variance)
Modify model structure (additional features might help)	Feature subset selection (reduce the number of input features)
Modify input features Adding more training data is usually not helpful	Decrease model complexity Reduces computational time Helps to reduce variance, but also increases bias

What are the problems for the underfitting and overfitting models?

What are the solutions?

Underfitting

• Problem: assumption of linear model not correct

• Choose a non-linear model

  • Polynomial regression

  • Regression splines

Overfitting

• Problem: Model too much adjusted to training data

  • High number of (irrelevant) input features

  • Number of data points not large enough

• Regularization: Can be useful for high-dimensional feature spaces

Regularization types

Ridge Regression

Lasso Regression

Ridge Regression

• Penalty term proportional to square of the coefficients

• Find best parameters to minimize the cost function

  • Tuning parameter controls the relative impact of the penalty term

  • Penalty term shrinks the estimated coefficients towards zero

• Effect of regularization as λ increases:

  • Variance is reduced

  • Bias can increase significantly

Lasso Regression

• Penalty term proportional to absolute value of coefficients

• Some of the parameters are set to exactly 0 with increasing tuning parameter

  • Selection of most important features

  • Increased model interpretability

Classification algorithm

k-Nearest-Neighbor

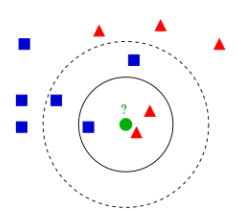
How to assign a class label to a new data point given some training data?

The k-Nearest-Neighbor algorithm is a very intuitive approach for classification.

• No learning of a model is necessary

• Assigning of class labels for unknown data is solely based on the training data

How to assign a class label to a new data point given some training data?

1. Choose the number k of neighbors

2. Calculate the distance (e.g Euclidean distance) from the data point to the training data points

3. Take the k nearest neighbors

4. Majority voting to determine the class assigned to the data point

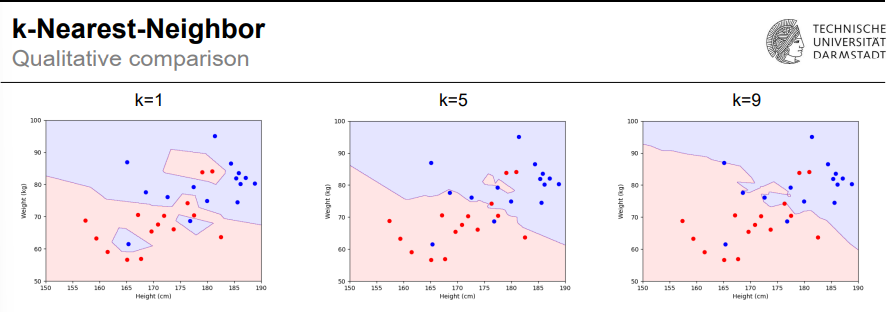
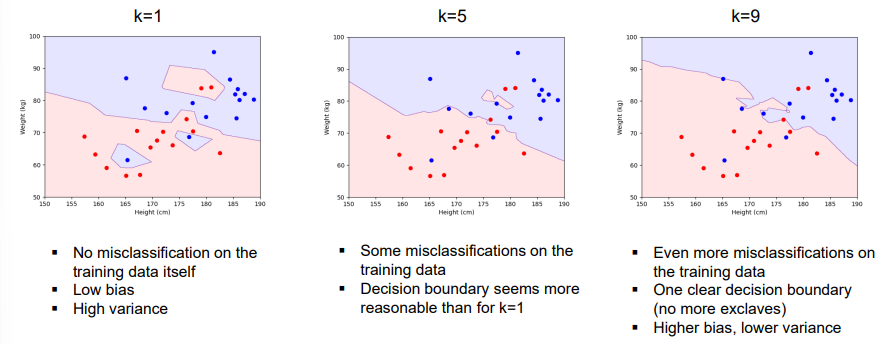
What are the Evaluation of Learned Models?

• Validation through experts

  • a domain expert evaluates the plausibility of a learned model

  • + often the only option (e.g., clustering)

  • - subjective, time-intensive, costly

• Validation on data

  • evaluate the performance of the model on a separate dataset drawn from the same distribution as the training data

  • + fast and simple, no domain knowledge needed, methods for re-using training data exist (e.g., cross-validation)

  • - labeled data are scarce, could be better used for training

• On-line Validation

  • test the learned model in a fielded application

  • + gives the best estimate for the overall utility

  • - bad models may be costly

Binary classification

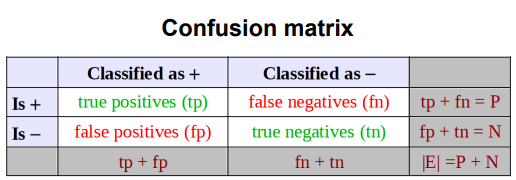
What is confusion matrix?

• It is for validation on data

• Define one class as positive class (+)

• Define the other class as negative class (-)

• Most common evaluation metric for binary classification:

  • Accuracy: acc= (tp+tn) / (tp+fn+fp+tn)

Validation on Data

Typically, the dataset is split into three parts:

1. Training data: data that is used to train the algorithm

2. Validation data: data that is used to optimize the hyperparameters of the model

3. Test data: data that is used to test the final model – never seen by the algorithm before

Validation on Data

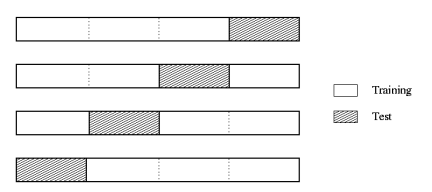
k-fold-Cross-Validation

1. Partition your dataset into 𝑘 equal subsets (e.g. with 𝑘 = 10)

2. For every partition:

   • Keep the partition as test set and use the other k-1 partitions as training data

   • Train the model and evaluate its performance on the test set

3. Average the results

   1. + Makes best use of the data • No influence of random sampling

   2. - Computationally expensive