Advanced Mathematics (Year 11 Syllabus)

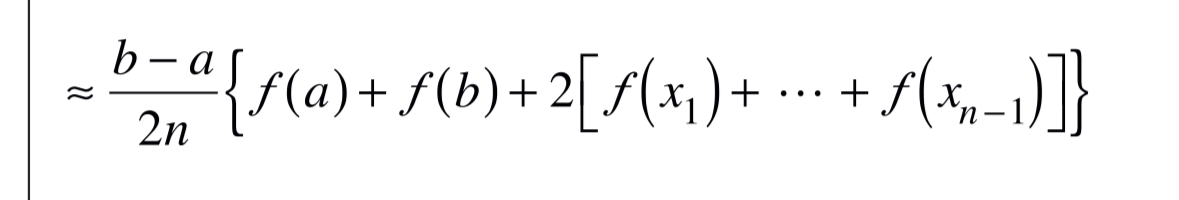
Trapezoidal Rule

Concepts Of Understanding:

b = x value of second end point.

a = x value of first end point.

n = number of sub intervals (remember that five points means four sub intervals).

f(…) = y values of points, thus why in the tables you get x and f(x) as it is like a graph. So if you have the shape, it is values of vertical lengths.

h = width of the individual sub interval. Formula on sheet already accounts for h/2 as h = 0.5 hrs b - a / n

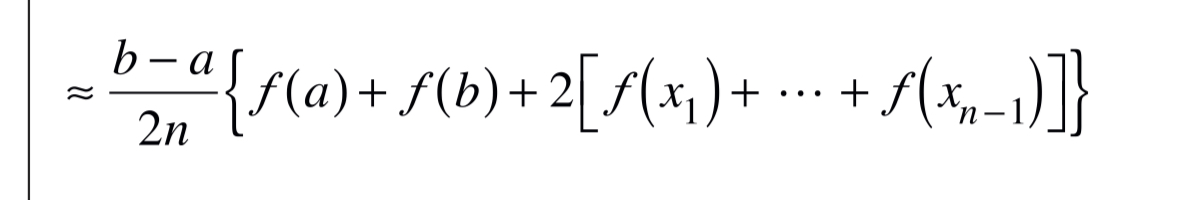
Completing The Square

Concepts Of Understanding:

Purpose: Convert quadratic to vertex form

Remember:

• Add (b/2)² to both sides. This will allow you to complete the square with one (b/2)² and determine vertical shift with the other.

• Ensure coefficient of x² is one.

Trig Identities

cotθ = cosθ/sinθ

sin²θ + cos²θ = 1

tan²θ + 1 = sec²θ

1 + cot²θ = cosec²θ

Log Laws

Product Law (1)

log_bMN = log_bM + log_nN

log₁₀12 = log₁₀6 + log₁₀2

Quotient Law (2)

log_bM/N = log_bM - log_bN

log₁₀8/2 = log₁₀8 - log₁₀2

Power Law (3)

log_bMⁿ = n x log_bM

log₂4³ = 3log₂4

Log Of 1 (4)

log_b1 = 0

log₇1 = 0

Categorical and Numerical Data

Categorical: Data that cannot be measured.

Numerical: Data that can be measured or counted. Discrete (exact number value and can be counted) and Continuous (usually rounded off).

Mathematical Mappings

Functions: One to One and Many to One (pass vertical line test).

Not Functions: One to Many and Many To Many (do not pass vertical line test).

Probability

P(A and B): P(A) x P(B)

P(A or B): P(A) + P(B) - P(A and B)

P(A given B) : P(A and B) / P(B)

Probability Tree Diagram

Probability Of An Outcome (Single Branch):

P(Outcome) = Multiply along the branch

Total Probability Of An Event (Multiple Branches):

P(Outcome) = Add probabilities of single branches

Conditional Probability:

You know the formula. Fill it in using branches.

Complement Rule

P(Not A) = 1 - P(A)

Probability Distribution

The Expected Value, E(X), of a probability distribution calculated the centre or mean μ. It is the sum of each possible value multiplied by its probability.

E(X) = μ = Σ x p(x)

Variance

Σ[x(squared)p(x)] - [E(X)](squared)

Standard Deviation

σ = square root of variance

Arc Length, Sectors and Segments

Arc Length Formula: l = θ/360 × 2πr

Area Of Sector: θ/360 x πrsquared

Perimeter Of Sector: 2r + Arc Length

Area Of Triangle: ½ x r squared x Sinθ

Area Of Segment:

½ x r squared x (θ - Sinθ)

Remember…

θ must be in radians.

Converting Between Degrees and Radians

Radians = π/180 x Degrees

Degrees = 180/π x Radians

Just remember that π radians = 180°

Bearings

True Bearings

• Always measured clockwise from North.

• Always given as a 3 digit number. For example, 60 degrees is 060 degrees.

Compass Bearings

• Use compass directions. For example N30degreesE

Remember it is not all SOH CAH TOA.

Use Sin and Cosine Rule. Usually with the occasional right angle triangle.

Congruence

SSS = Side Side Side

SAS = Side Angle Side

AAS = Angle Angle Side

RHS = Right Angle Hypotenuse Side

Similar Triangles

Sketching Derivatives

Trigonometric Equations

Lists and Venn Diagrams

Odd, Even and Composite Functions