5- Linear inhomogeneous differential equations

What is the general form of a second-order linear inhomogeneous ODE with constant coefficients?

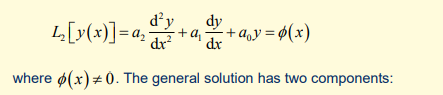
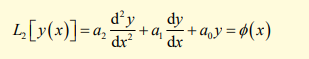
What are the two components of the general solution to a second-order inhomogeneous ODE?

• Complementary function y_c(x): Satisfies the homogeneous equation L₂[y_c(x)] =0

• Particular integral y_p(x): A specific solution that satisfies L₂[y_p(x)]=ϕ(x)

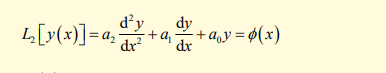
How is the general solution to the inhomogeneous ODE formed?

The general solution is the sum of the complementary function and the particular integral:

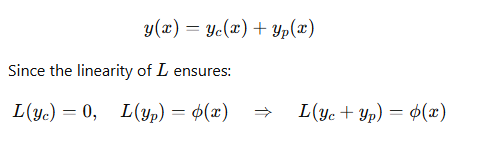
How is the complementary function y_c(x) determined?

What is the purpose of the particular integral y_p(x)?

• Its a specific solution that accounts for the inhomogeneous term ϕ(x)

• It ensures that the full equation L(y)=ϕ(x) is satisfied.

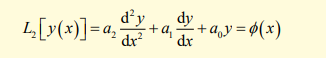
What is the method used to find the particular integral?

The method of undetermined coefficients

• This nvolves guessing a trial solution with unknown constants and determining their values by substitution.

What is the basic idea behind the method of undetermined coefficients?

1. Assume a trial solution y_p(x) with unknown constants.

2. Substitute y_p(x) into the differential equation.

3. Solve for the unknown coefficients to satisfy the equation.

What is the key requirement for using the method of undetermined coefficients?

This method only works if ϕ(x) is a polynomial, exponential, sine, or cosine function (or a combination of these).

Table used for the method of undertermined coefficients

What should you do if a term in the trial solution y_p(x) is already present in the complementary function y_c(x)?

Multiply the trial solution by x^m, where m is the lowest power that ensures no term in y_p(x) duplicates y_c(x).