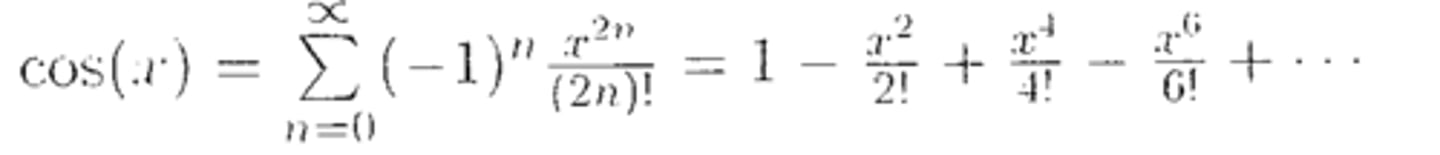Calculus 2: Series Tests
1/12
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
13 Terms
Test for Divergence
Series Type: ALL
When to try: First
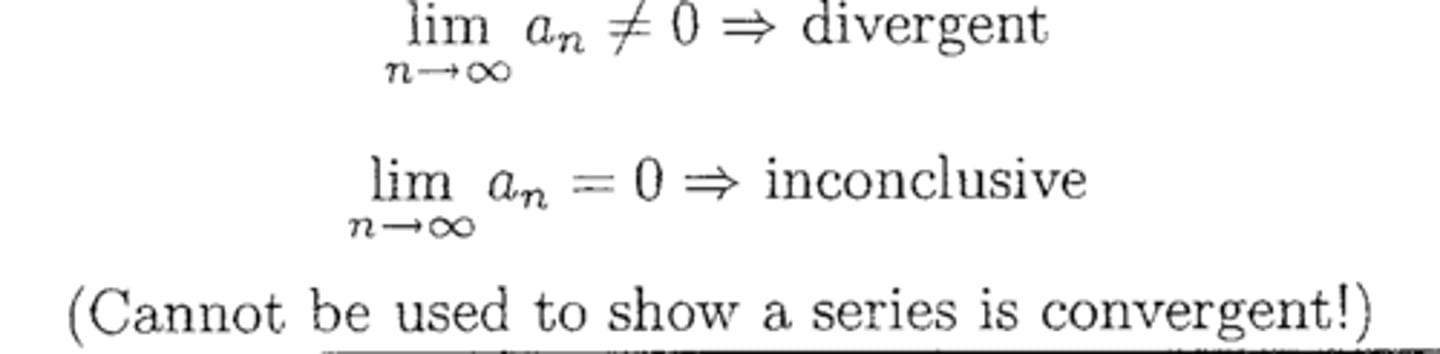
Geometric Series
Series Type: Sum(1..Inf) a*r^(n-1)
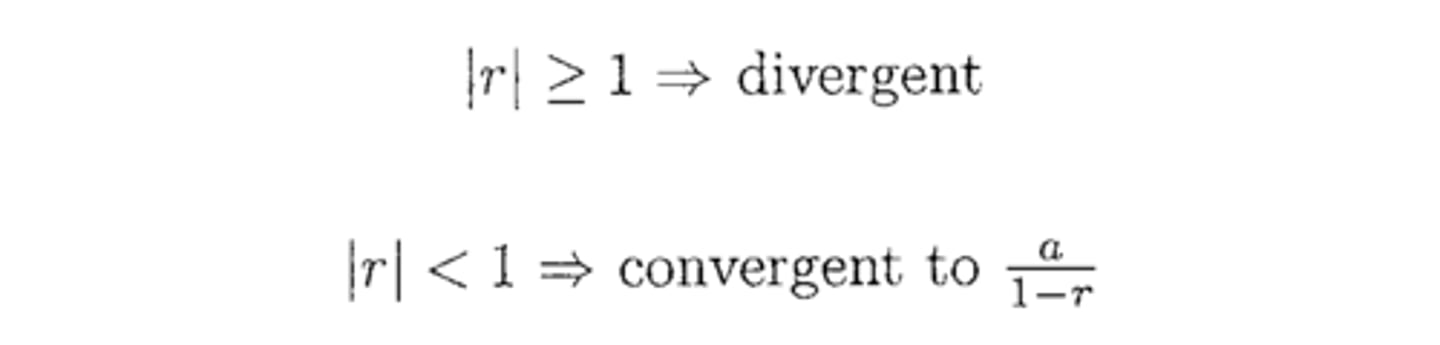
Integral
Series type: f(n) is positive, continuous, decreasing
When to try: f(n) must be integrable
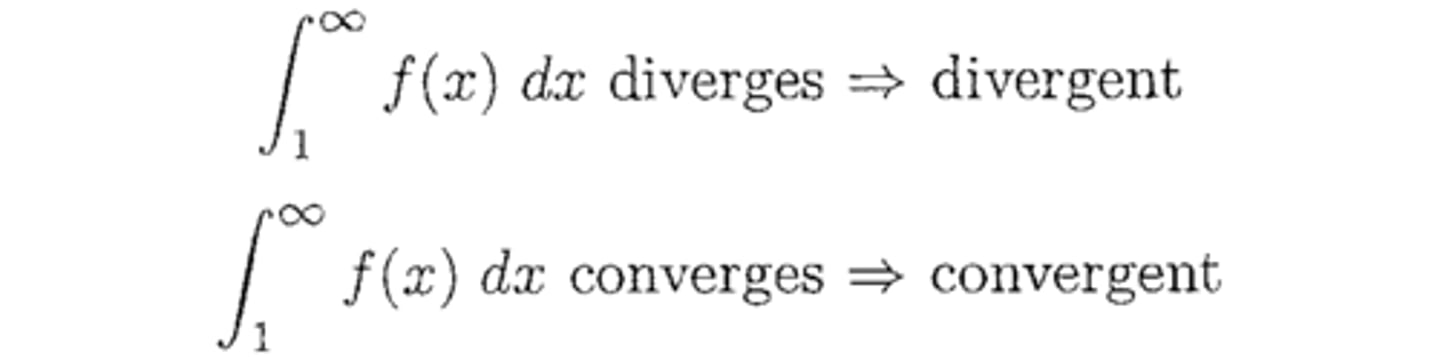
P-Series
Series type: Sum(1..Inf) 1/(n^p)
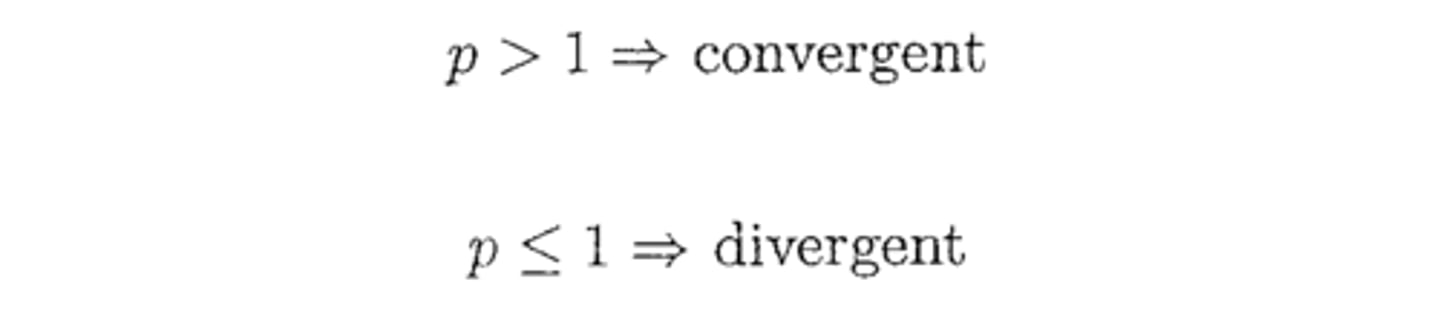
Direct Comparison
Series type: An and Bn are positive
When to try: If it looks close to a p-series or geometric
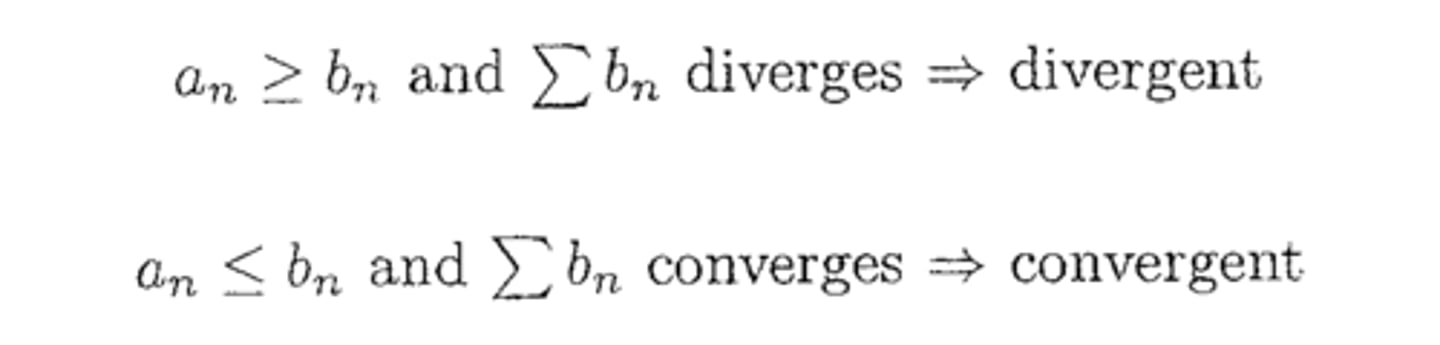
Limit Comparison
Series type: An and Bn are positive
When to try: if a Direct Comparison Test does not work
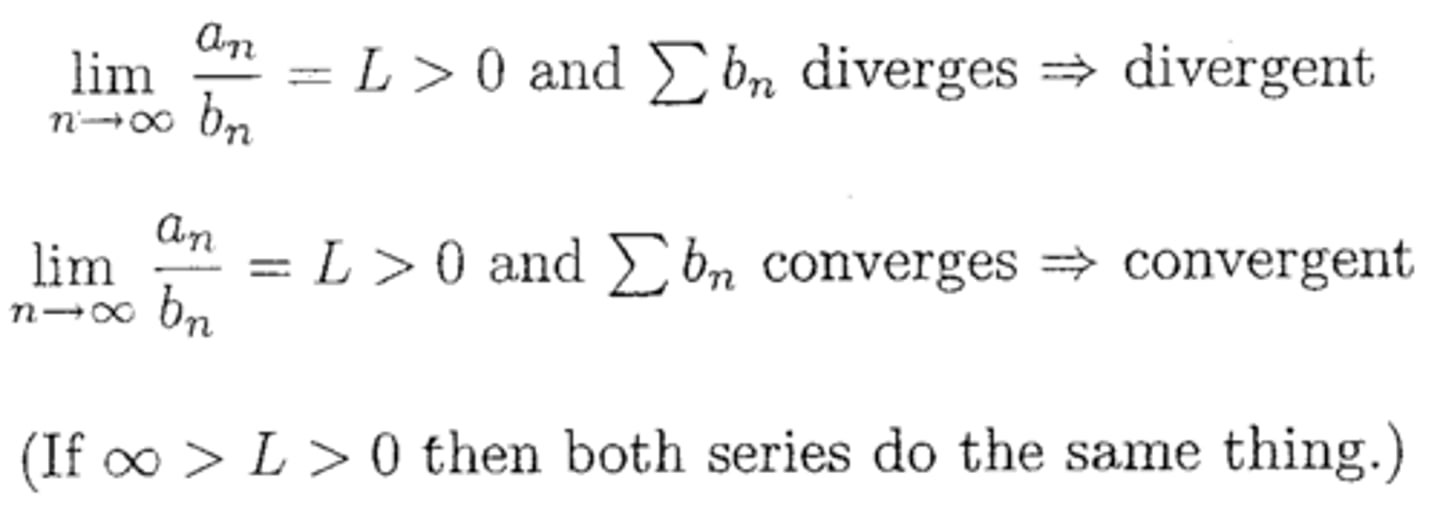
Alternating Series
Series type: Sum(1..Inf)(-1^(n-k))*Bn
* Use test for divergence if limit does not equal 0

Absolute convergence
Series type: ALL
When to try: With trig. series or some alternating series
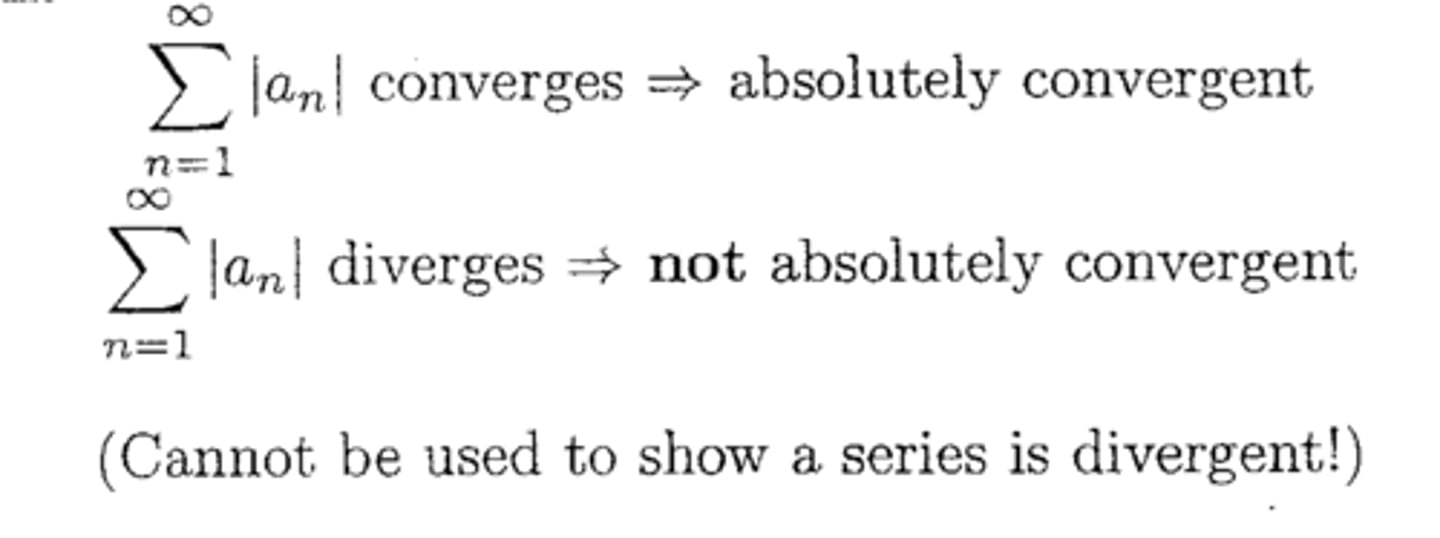
Ratio Test
Series Type: All
When to try: With factorials or exponentials
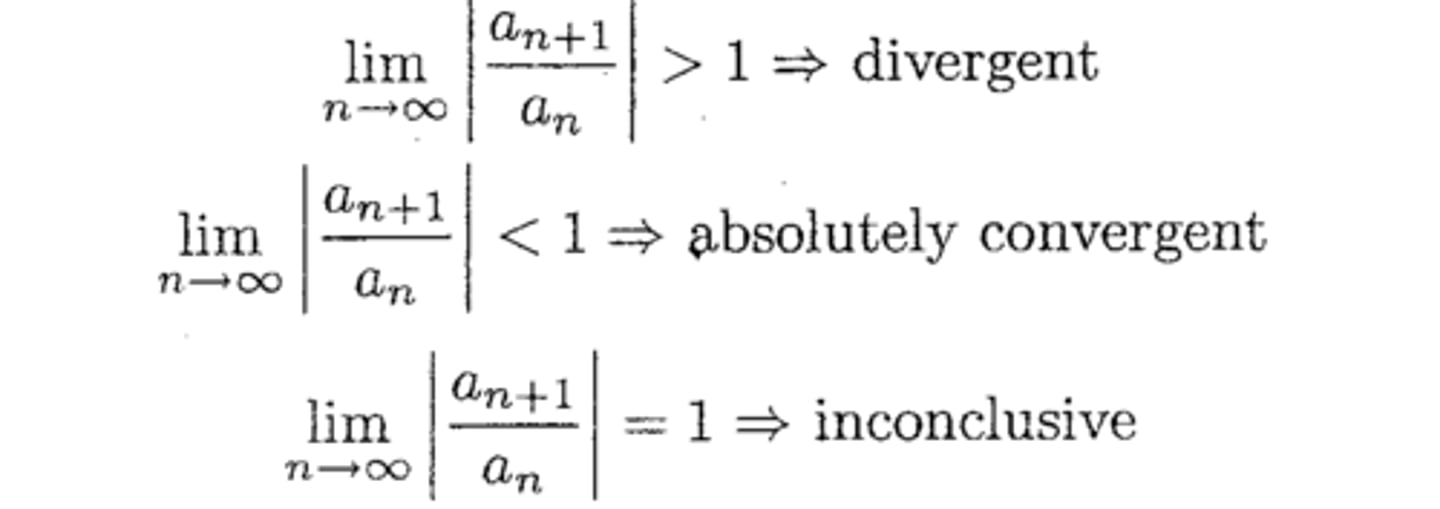
Series Expansion: 1/(1-x)
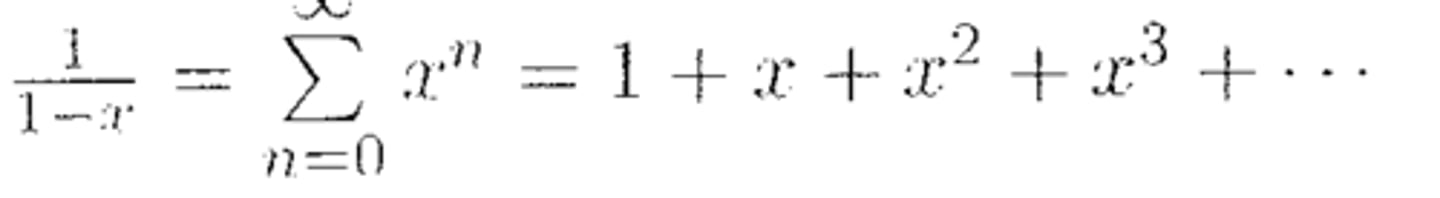
Series Expansion: e^x
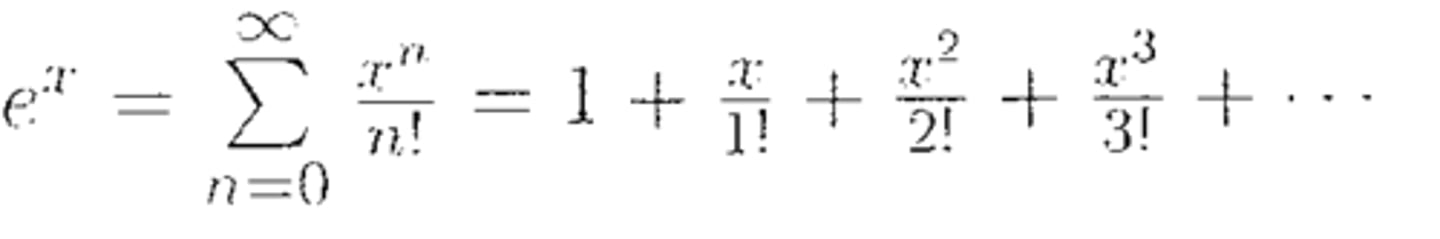
Series Expansion: Sin(x)
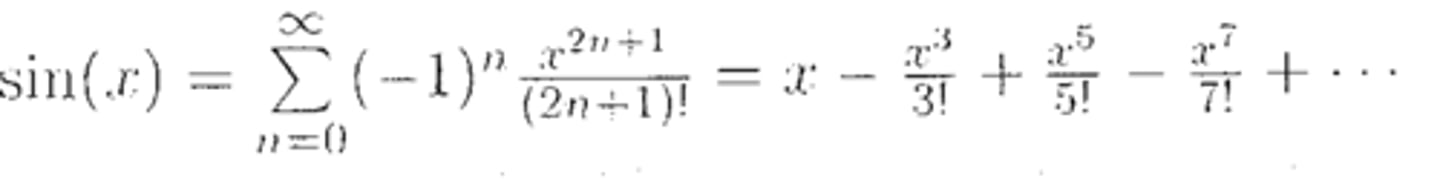
Series Expansion: Cos(x)