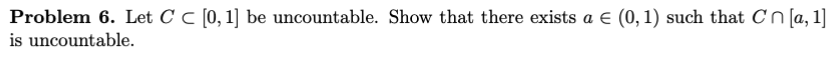Foundations of Analysis Exam #1

Supremum

Axiom of Completeness

Bounded

Lemma 1.3.8 (Supremum Lemma)

Surjective

Injective

Squeeze Theorem

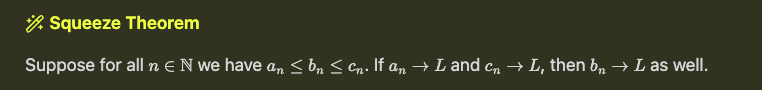
Theorem 1.4.1 (Nested Interval Property)

Sequence

Subsequence

Theorem 2.5.2 (Convergence of Subsequences)

Trianle Inequality

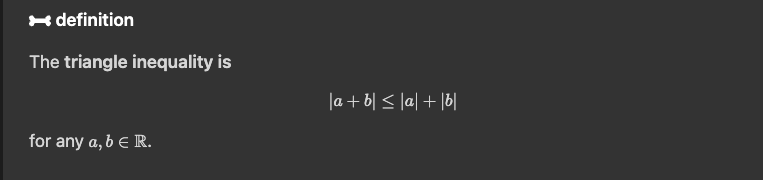
Reverse Triangle Inequality

Cardinality

Theorem 1.5.6 (Countability of R)

R is uncountable lol

Theorem 1.5.7 (Countability of subsets)

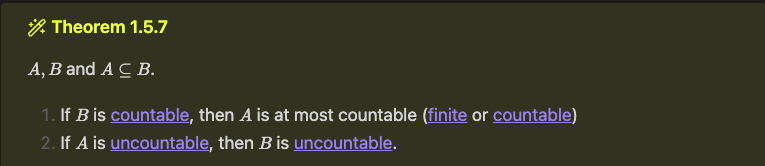
Archimedean Property #1

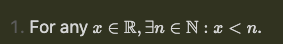
Archimedean Property #2

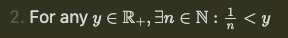
Countable

uncountable

Theorem 1.5.8 (Unions of countable sets)

Monotone

A sequence is monotone if it is strictly non-decreasing or non-increasing

Limit Superior

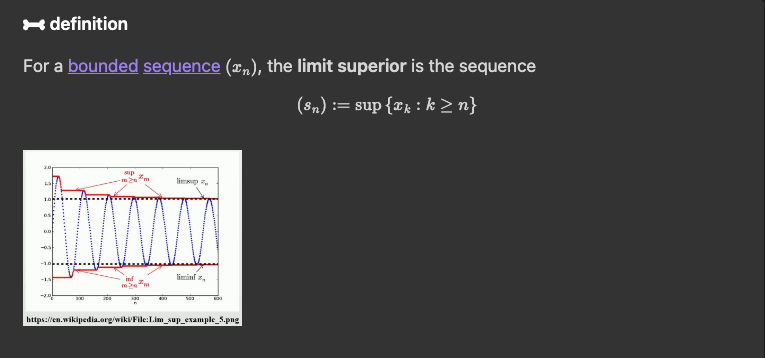
Limit inferior

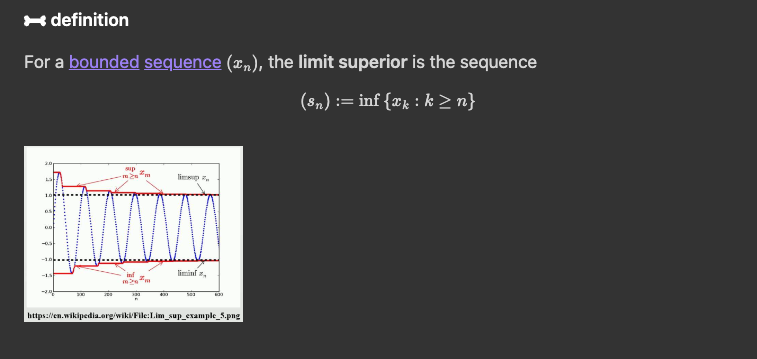
Finite

Cauchy

Theorem 2.6.2 (Cauchy sequences’ convergence)

Lemma 2.6.3 (Boundedness of Cauchy Sequences)

Theorem 2.6.4 (Convergent sequences’ Cauchy-ness)

the 4 Algebraic Limit Theorems (2.3.3)

Theorem 1.5.6.1 (Countability of Q)

Q is countable

Theorem 2.5.3 (Bolzano Weierstrauss Theorem)

Theorem 2.3.2 (Boundedness of convergent sequences)

Every convergent sequence is bounded. The converse is not true.

Theorem 2.3.4 (Order Limit Theorem)

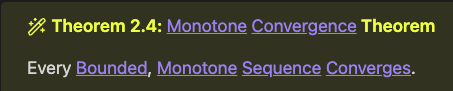
Theorem 2.4 (Monotone Convergence Theorem)

Upper Bound

Equivalence Relation

Two sets are equivalent if they have the same cardinality.

Convergent

Theorem 2.2.7 (Sequences have one limit)

Integer Spacing Lemma

Corollary 1.4.4 (existence of irrationals)

HW#1 Problem #6 (Supremum in the set)

If a is an upper bound for A, and a in A, then a = sup A.

HW#1 Problem #5 (Supremum of a superset)

For nonempty, bounded above, A,B in R with B subseteq A. Then, supB <= supA

HW#2 problem #2

HW#2 Problem #6 (Supremum of sets of integers)

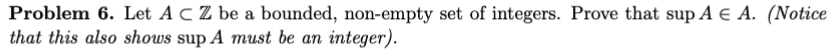
HW#3 Problem #1 (supremum of nonempty, finite sets)

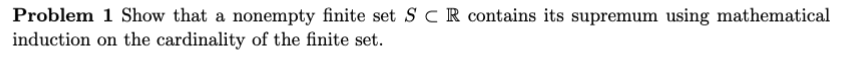
HW #3 #2 (ARchimedean infimum)

HW#6 Problem #6 (intersections of uncountable sets)