physics - motion & forces (2.1 - 2.33)

2.1 scalar quantities

magnitude (size)

no specific direction

2.2 vector quantities

magnitude (size)

specific direction

2.3 scalar vs vector quantities

scalar: only magnitude

vector: magnitude & direction

2.4 examples of scalar quantities

distance

speed

mass

energy

2.4 examples of vector quantities

displacement

velocity

acceleration

force

weight

momentum

2.5 velocity definition

speed in stated direction

2.6 speed equation

speed (m/s) = distance (m)/time (s)

s = d/t

2.7 distance/time graphs

horizontal line: object stationary

straight, sloping line: object travelling at constant speed

steeper line = object travelling faster

speed = gradient of line

• gradient = Δy/Δx = d/t = s

2.8 acceleration equation

acceleration (m/s^s) = change in velocity (m/s)/time (s)

a = (v-u)/t

2.9 (final velocity)² - (initial velocity)² equation

(final velocity)² (m/s)² - (initial velocity)² (m/s)² = 2 x acceleration (m/s²) x distance (m)

v² - u² = 2ax

2.10 velocity/time graphs

horizontal line: object travelling at constant velocity

negative velocity (below x axis): object moving in opposite direction

2.10 velocity/time graphs - compare acceleration from gradients

sloping line: object accelerating

steeper line = greater acceleration

line sloping down to right: object decelerating

2.10 velocity/time graphs - calculate acceleration from gradient

acceleration = gradient of line

• gradient = Δy/Δx = (v-u)/t = a

2.10 velocity/time graphs - find distance travelled

distance travelled = area under graph

• s x t = d

2.11 determining speed of objects using light gates

to measure speed - need distance & time

light gates measure time (more accurate than stopwatch)

2.12 typical everyday speeds

walking: 1.4 m/s

cycling: 6 m/s

speed limit in towns: 6 m/s

ferry: 18 m/s

motorway speed limit: 31 m/s

commuter train: 55 m/s

high speed train: 90 m/s

airliner: 250 m/s

2.13 acceleration in free fall

10 m/s²

2.14 Newton’s 1st law

moving object will continue to move at same speed & direction unless external force acts on it

stationary object will remain at rest unless external force acts on it

2.14 Newton’s 1st law - resultant force = 0

balanced forces = 0 resultant force

won’t change velocity of object

2.14 Newton’s 1st law - resultant force ≠ 0

unbalanced forces = non-0 resultant force

will change speed and/or direction of object

2.15 Newton’s 2nd law

acceleration of object directly proportional to force acting on it & inversely proportional to its mass

acceleration in direction of resultant force depends on:

• size of force (same mass: bigger force = bigger acceleration)

• mass of object (same force: bigger mass = smaller acceleration

2.15 force equation (Newton’s 2nd law)

force (N)= mass (kg) x acceleration (m/s²)

F = ma

2.16 weight definition

measure of pull of gravity on object

2.16 weight equation

weight (N) = mass (kg) x gravitational field strength (N/kg)

W = mg

2.17 how is weight measured?

using force meter - has scale in newtons

2.18 relationship between weight of body & grav. field strength

earth’s grav. field strength = 10 N/kg

each kg experiences force of 10N

2.19 core practical: relationship between force, mass & acceleration - how mass affects acceleration (masses on trolley)

1. prop up one end of ramp; place trolley on ramp

2. set up light gates & pulley & string

3. stick card to top of trolley; measure length of card

4. release trolley from top of ramp; record speed of trolley & time taken to go from 1st → 2nd light gate

5. put mass on trolley & repeat step 4

6. add mass to trolley; repeat step 5

2.19 core practical: relationship between force, mass & acceleration - how force affects acceleration (masses on trolley)

1. prop up one end of ramp; place trolley on ramp

2. set up light gates & pulley & string

3. stick card to top of trolley; measure length of card

4. add masses to trolley

5. release trolley from top of ramp; record speed of trolley & time taken to go from 1st → 2nd light gate

6. take 1 mass off trolley & put on end of string; repeat step 5

7. continue until all masses on trolley on end of string

2.20 object moving in circular orbit at constant speed

constant speed, changing velocity

moving at same speed, constantly changing direction

so accelerating (changing direction)

2.21 centripetal force

resultant force that acts towards centre of circle & causes change in direction (for object moving in circle)

2.22 inertial mass

measure of how difficult it is to change velocity of object

more massive object = need more force to change its velocity

inertial mass of object = force on it/acceleration force produces

2.23 Newton’s 3rd law

forces on 2 different objects when they interact with each other

objects can be touching (person & chair)/at distance (earth & moon)

for every action there is an equal & opposite reaction

2.23 Newton’s 3rd law - equilibrium situations

pair of forces on 2 interactive objects (action-reaction forces)

2 forces: same size, opposite directions

2.23 Newton’s 3rd law - collision interactions

action & reaction forces during collision:

• same size

• don’t necessarily have same effect - objects are diff. masses

2.23 Newton’s 3rd law - conservation of momentum

total momentum of both objects before collision = total momentum of both objects after collision

momentum lost by object 1 = momentum gained by object 2

momentum is conserved

2 objects moving opposite directions - 1 has positive & 1 has negative momentum

action-reaction forces vs balanced forces

action-reaction forces: act on different objects

balanced forces: act on same object

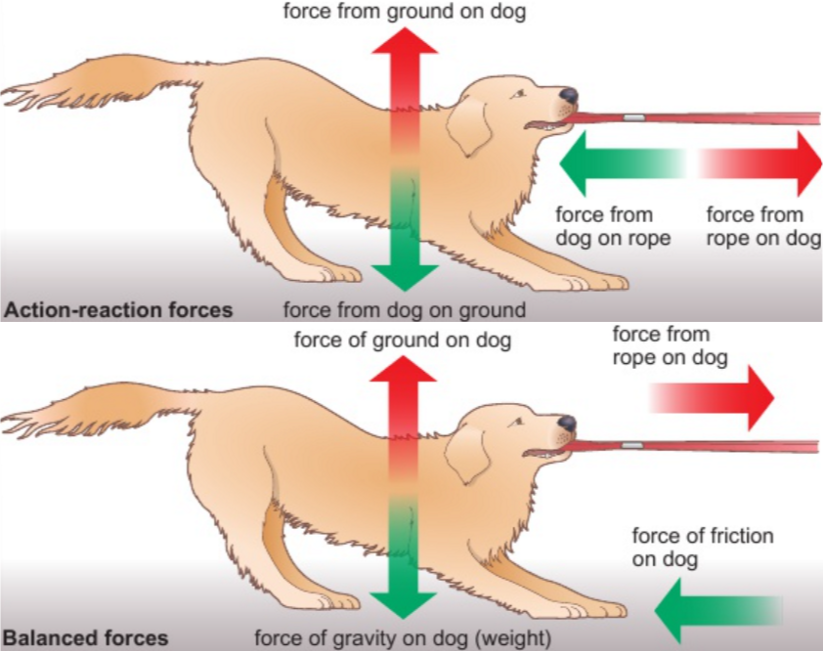
2.24 momentum definition

measure of tendency of object to keep moving/how hard it is to stop it moving

2.24 momentum equation

momentum (kg m/s) = mass (kg) x velocity (m/s)

p = mv

2.25 examples of momentum in collisions

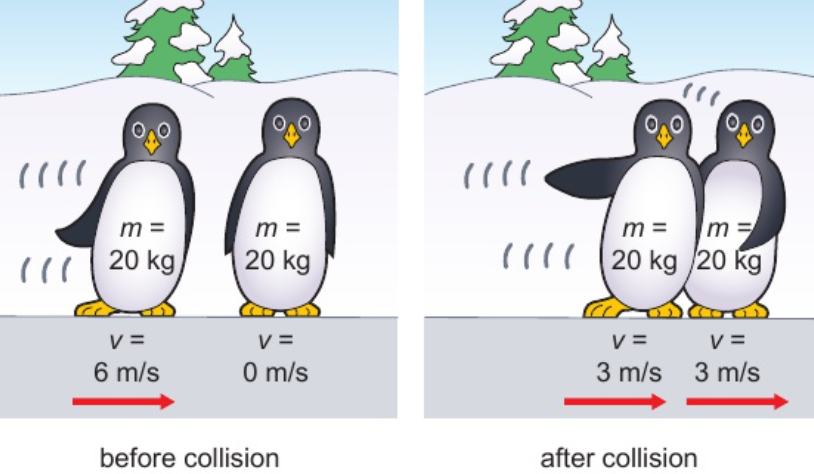
2.26 force equation (Newton’s 2nd law)

force (N) = change in momentum (kg m/s)/time (s)

F = (mv - mu)/t

reaction time

time between person detecting stimulus & their response

2.27 methods of measuring human reaction times

computers, electric circuits - measure time between stimulus & response

2.27 typical results of human reaction times

visual stimulus - 0.25s

2.28 vehicle’s stopping distance

thinking distance + braking distance

2.29 factors affecting vehicle’s stopping distance

vehicle’s mass: more mass = more force to decelerate = greater s.d.

vehicle’s speed: greater speed = greater s.d.

driver’s reaction time: greater reaction time = greater s.d.

state of vehicle’s brakes: worn brakes = less friction = greater s.d.

state of road/amount of friction between tyre & road: wet road/loose gravel = less friction = greater s.d.

2.30 factors affecting driver’s reaction time

drugs/alcohol

tiredness

illness

distractions (e.g. phone)

2.31 dangers caused by large decelerations

large deceleration requires large force (on vehicle)

F = ma: a increases → f increases

2.31 forces in typical situations on public road

e.g. 1500kg car crashes at 15 m/s, stops in 1s

F = (mv - mu)/t

((1500 × 0) - (1500 × 15))/1

= -22500/1

= -22500N

2.32 stopping distances over range of speeds

20mph = 12m

30mph = 23m

40mph = 36m

50mph = 53m

60mph = 73m

70mph = 96m

work done definition

energy transferred by force acting over a distance

work done equation

work done (J) = force (N) x distance moved in direction of force (m)

E = Fd

kinetic energy definition

energy stored in moving object

kinetic energy equation

kinetic energy (J) = ½ x mass (kg) x speed² (m/s)²

KE = ½mv²

2.33 braking distance, work done, kinetic energy

work done to stop vehicle = initial kinetic energy

braking distance depends on kinetic energy so depends on (initial velocity)²

e.g. velocity doubles → braking distance x 2² = 4