geometric vectors - parts 2

coursera course about linear algebra week1

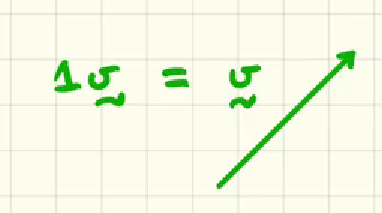
if v (1v) is the vector in the image, this means that his “scalar coefficient is 1”… what graphically would be a vector like 2v?

the 2v vector would have twice the magnitude of v and point in the same direction. Graphically, it would be represented as a line segment that is twice the length of vector v, maintaining the same orientation.

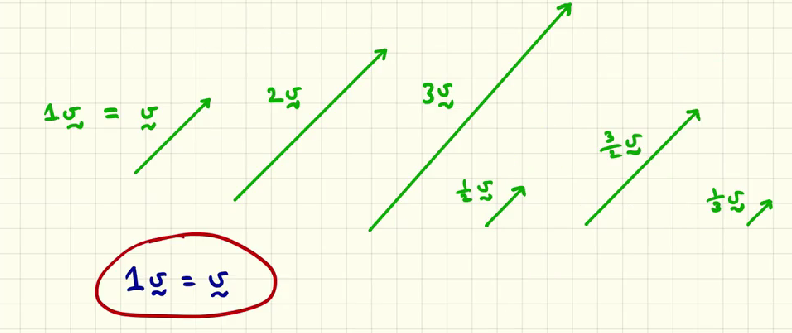
when we talk about vector multiply by a scalar, what happen if the scalar is negative? what if multiplied by -1, what if by -3?

if the scalar is negative, the resulting vector points in the opposite direction of the original vector while having the same magnitude.

if we multiply a vector by a negative scalar (-1) what happend?

The resulting vector points in the opposite direction while maintaining the same magnitude as the original vector. (if the negative scalar is -1), if the scalar was -3 as the case of -1 the direction would be as well the opposite of the original vector and the magnitude should be 3 times the ones of the vector

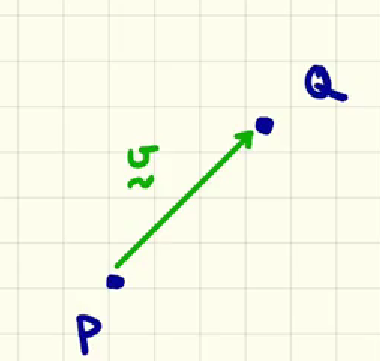
if v is the vector PQ in point notation, what would be the vector -v?

the -v vector in point notation would be QP, meaning that it would start now in Q and terminates at point P. And it would have the same magnitude as vector v but in the opposite direction.

This would mean that if we do “v + (-v)” we are saying that we are adding a vector to its negative counterpart, which results in the zero vector or in other words in PP which is a vector that starts in P and terminate in P which is a zero-length vector.

what happened if we add a vector to its negative?

The sum of a vector and its negative results in the zero vector, which is a vector that point in every direction but has zero length.

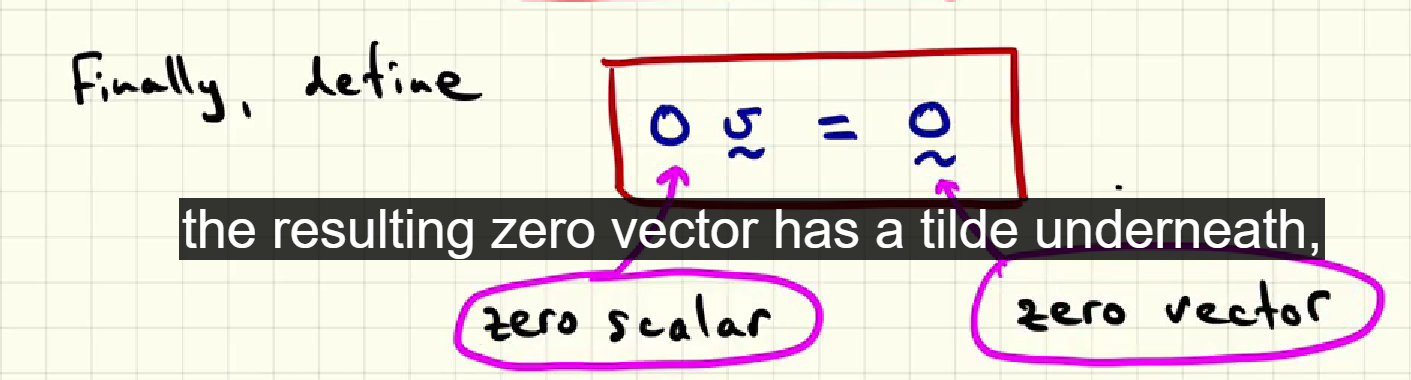
how we indicate a zero vector which is equal to 0v (in this case v was a vector)?

we indicate a zero vector using a notation that typically is 0 with a tilde underneath

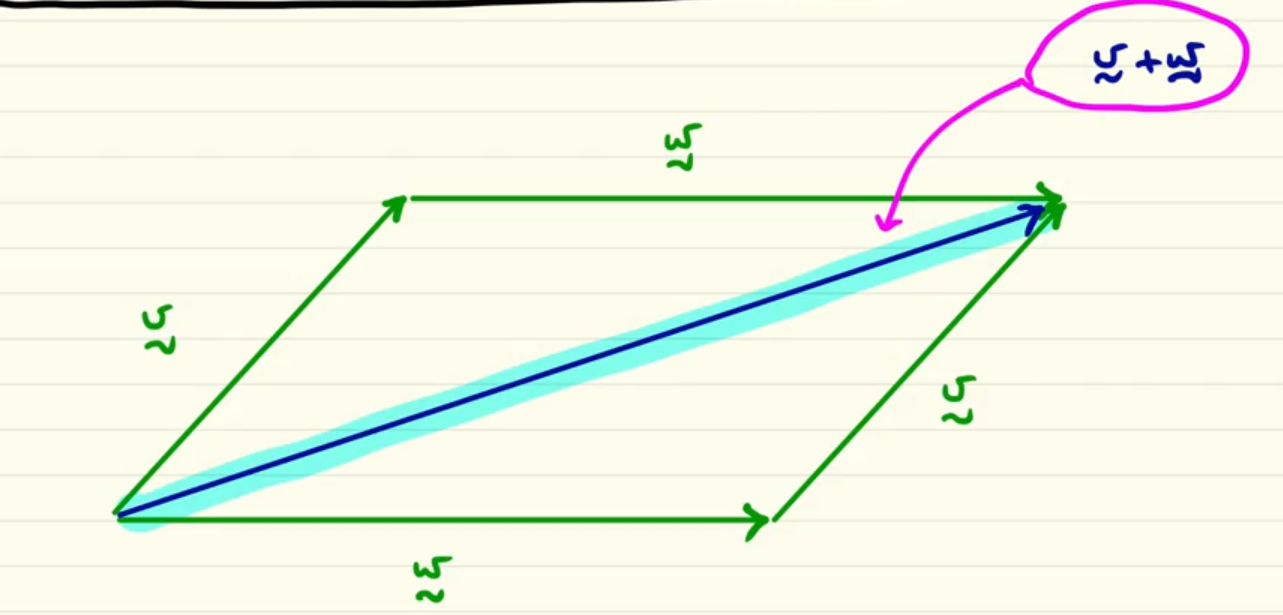
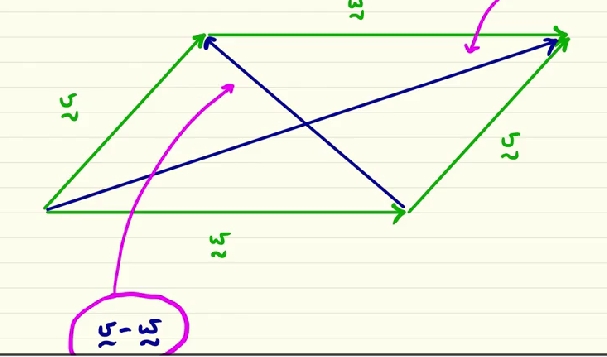
This image show the diagonal highlighted in lighblue as the v+w sum using the parallelogram law… what would be the v-w (which is the difference between the vector v and the vector w)?

This diagonal show the difference between v and w… as we can se is the path that indicate the resulting vector from v to w, starting at the tip of v and ending at the tip of w. since we do the difference, or in other words we add (-w) the path differ from the sum of v+w!