Week 2: Quantum Model of Atom (7.4-7.7 -excluding particle in box)

Atomic spectroscopy :

is the study of the light absorbed and emitted by atoms when an electron makes a transition from one energy level to another.

The wavelengths absorbed or emitted depend :

on the energy differences between the levels involved in the transition; large energy differences result in short wavelengths and small energy differences result in long wavelengths.

Atomic spectroscopy :

is the study of the light absorbed and emitted by atoms when an electron makes a transition from one energy level to another.

The wavelengths absorbed or emitted depend :

on the energy differences between the levels involved in the transition; large energy differences result in short wavelengths and small energy differences result in long wavelengths.

Electrons have a wave nature with an associated

wavelength, as quantified by the de Broglie relation.

The wave nature and particle nature of matter are complementary—

the more you know of one, the less you can know of the other.

The wave–particle duality of electrons is :

quantified in Heisenberg’s uncertainty principle

Heisenberg Uncertainty Principle:

• which states that there is a limit to how well we can know both the position of an electron (associated with the electron’s particle nature) and the velocity times the mass of an electron (associated with the electron’s wave nature)

• the more accurately one is measured, the greater the uncertainty in measurement of the other.

The inability to simultaneously know :

both the position and the velocity of an electron results in the inability to predict a trajectory for an electron.

electron behaviour is described :

• differently than the behaviour of everyday-sized particles.

• The trajectory we normally associate with macroscopic objects is replaced, for electrons, with statistical descriptions that show, not the electron’s path, but the region where it is most likely to be found.

The particle in a one-dimensional box:

• is one of the simplest quantum-mechanical systems we can think of.

• In contrast, an electron or electrons in atoms are far more complicated mathematically.

Applying the Schrödinger equation treatment to a particle

• in a one-dimensional box is instructive to understanding quantization of the atom.

• The confinement of a particle in a box (or an electron to an atom) results in quantization of the energy levels in the quantum-mechanical system.

The most common way to describe electrons in atoms according to quantum mechanics is :

• to solve the Schrödinger equation for the energy states of the electrons within the atom.

• When the electron is in these states, its energy is well defined but its position is not.

• The position of an electron is described by a probability distribution map called an orbital.

The solutions to the Schrödinger equation for a hydrogen atom (including the energies and orbitals) are characterized by three quantum numbers

n, l, and ml

The principal quantum number (n) determines:

the energy of the electron and the size of the orbital

the angular momentum quantum number (l) determines

the shape of the orbital

the magnetic quantum number (ml) :

determines the orientation of the orbital.

An electron configuration for an atom simply shows

• which atomic orbitals are occupied by the atom's electrons.

• For example, the electron configuration of helium (1s^2) shows that helium's two electrons exist within the 1s orbital.

The order of filling atomic orbitals in multielectron atoms is as follows:

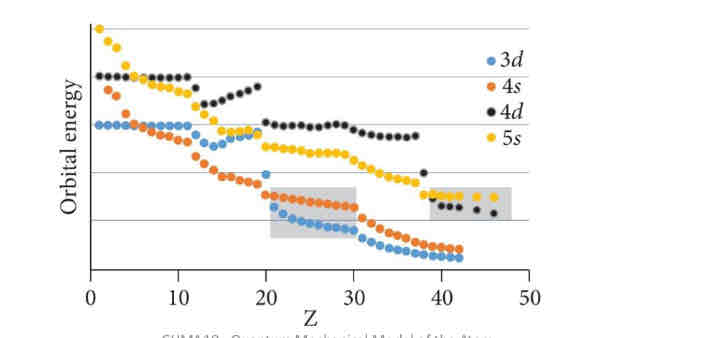
1s 2s 2p 3s 3p [4s 3d] 4p [5s 4d] 5p 6s.

Beginning in period 4, the ns orbitals are

• lower in energy than the (n - 1)d orbitals; however, the (n - 1)d orbitals are lower in energy than the ns orbitals.

• However, because they are so close in energy, for most transition elements the ns orbitals are populated even though the (n - 1)d orbitals are not full.

• For example, all the first-row transition metals have 4s-3d^x except Cr and Cu, which only have one 4s electron

The reason the higher energy 4s orbitals are populated in the transition elements is because

by putting one or more electrons in the ns orbitals, electron-electron repulsion is relieved in the (n - 1)d orbitals.

According to the Pauli exclusion principle:

each orbital can hold a maximum of two electrons with opposing spins.

According to Hund's rule

orbitals of the same energy first fill singly with electrons with parallel spins, before pairing.

The electron configuration of an ion can be determined by :

adding or subtracting the corresponding number of electrons to or from the electron configuration of the neutral atom.

The electrons always come out of the:

• highest energy orbitals.

• The highest energy orbitals are those with the highest value of n.

Given the choice of electrons with the same value of n to remove the orbital with the highest / value is

depleted

The Bohr Atomic Model

• Niels Bohr (1885-1962) took Plank’s idea of quantization and applied it to atomic spectra

• It was known that molecules and atoms have very specific atomic spectra (colours)

• Bohr aimed to link spectral data (colours it displayed) to the underlying structure of a particular compound or atom by applying quantization to electrons

• In 1912, he developed a mathematical model of the atom with discrete energy levels or shells

  • Electrons release or emit light while moving between shells • Predicted hydrogen spectrum exactly!

formulas in ch 7

𝐄𝐧 = −𝐑𝐇 (𝟏/𝐧^𝟐)

• n = 1,2,3

• (rydberg constant ) RH = 2.18 x 10-18 J

Atoms have definite and discrete:

energy levels (orbital) in which an electron may exist without emitting or absorbing electromagnetic radiation

electron moves in:

circular orbit about nucleus and its motion is governed by ordinary laws of mechanics and electrostatics

RESTRICTION to electrons movement :

angular momentum of the electron is quantized i.e. it can only have certain discrete values

As the orbital radius increases,:

so does the energy i.e. the larger the orbital, the higher the energy level

Electron may move from:

• one discrete energy level (orbit) to another with energy difference expressed as

  • 𝛥𝐸 = −𝑅𝐻(1/𝑛𝑓^2 −1/𝑛𝑖^2 )

monochromatic radiation

is emitted or absorbed when an electron moves energy levels and the energy of light photons is given by ΔE = ℎ𝜈

ΔE = ℎ𝜈 (light absorbed vs emitted )

• ΔE > 0 when light is absorbed

• ΔE < 0 when light is emitted

Ground State:

• Atoms that have not absorbed any energy

• Where electrons are most stable

When electrons are excited to higher energy states,

• they release the energy absorbed to get back to the ground state

  • Energy released in the form of light

What was wrong with Bohr’s model:

it relied on electrons being particles and only re-produced the line spectra for 1 electron systems

What did louis de Broglie wonder

• “If light energy has particle-like properties, does matter have wave-like properties?”

• His suggestion was based on Einstein’s proof that light existed as discrete particles and he derived a relationship between momentum (the product of speed and mass) and wavelength for electrons 𝛌 =𝐡/𝐦𝐯

de Broglie hypothesized particles and waves:

• have the same traits E=mc^2 = hv

• substitute v for c -think real particles travel at lower speeds

• through the equation λ , de Broglie substituted v/λ for v and arrived at the final expression that relates wavelengths and particles with speed

  • λ =hv/mv^2 =h/mv

The problem was that de Broglie’s ideas

• were “ad hoc”, meaning that they were purely theoretical!

  • This is a bit discouraging for de Broglie but the scientific community has taken notice of his work

  • But in 1927, experimental evidence showed electrons diffract and produce an interference pattern in a double slit experiment just like light…electrons act like waves…what is happening?

    • De Broglie was right!

The more massive an object is:

the less the wave nature becomes

redo double slit experiment with electrons but use a laser detector to figure out which slit the electrons go through what is the result:

• no more diffraction: the wave nature of the electrons is gone!

• laser removes wavelength properties…they behave as a particle beam • How can we explain this?

  • Heisenberg Uncertainty Principle

What did Heisenburg ponder on:

• he was wrestling with how to explain wave-particle duality and why electrons seemed to change their nature depending on the experiment

• Evidence of dual particle/wave nature of the electron led Heisenberg to the Heisenberg Uncertainty Principle

Heisenberg Uncertainty Principle

• The act of measurement changes the properties of the electron (i.e. you can’t measure it without disturbing it

• impossible to determine simultaneously both position and velocity of an electron (or any other small particle)

• In other words, we cannot precisely specify where an electron of known energy is at any moment is time

Heisenburg Formula :

• ∆𝒙 ∙ 𝒎 ∙ ∆𝐯 ≥ 𝒉 / 𝟒𝝅 = 𝒄𝒐𝒏𝒔𝒕𝒂𝒏𝒕

• here Δx and Δv are the uncertainties in the position and velocity

• This equation tells us that the uncertainty in the speed or position of an object is inversely proportional to the mass

Even with his equation, Heisenburg still could not answer :

what does an atom look like

Erwin Schrondinger :

• latched onto the idea of electrons as waves and in 1925 came up a differential equation, now known as the Schrödinger equation, to describe an electron in an atom as a wave

• 𝐇𝛙 = 𝐄𝛙

• The solution to this equation is another equation that describes a wave: a wave function, 𝛙

• Describes both the particle and wave nature of the electron in a hydrogen atom

• Solutions give energy states and their corresponding wave functions

• Can be solved exactly for 1 electron systems but anything more than 1 electron solution must be estimated!

Max Born (1882-1970)

• was Heisenberg’s supervisor

  • Born had worked closely with Heisenberg to develop his ideas

  • Born realized that the wavefunction 𝜓 is not ideally suited to visualize the atom but based on his work with Heisenberg he realized that one can calculate a probability density for the electron by looking at the function 𝜓2

  • 𝜓2 gives a three-dimensional probability density plot for an electron’s position in space called an orbital

  • That is, we can calculate “shapes” that represent boundaries within which an electron should be found

  • This doesn’t violate the Heisenberg Uncertainty Principle

  • Born now had the tools to create a visual representation of electrons in an atom!

Each electron is described by 3 quantum numbers

n for energy, ℓ for angular momentum and m for spatial orientation

Ψ2 =

Ψ2 = probability density = probability/unit volume

Radial Probability equation

Radial Probability = (Probability / unit volume) times volume of shell

Radial Distribution Function:

• We divide up the space around nucleus into shells..sort of like an onion

• Now, the radial probability is defined as the probability of finding an electron in a given shell

  • Not within a certain radius!

Since we define the shell volume as zero at the nucleus

the probability of finding the electron also goes to zero

Atomic Orbital

• a three-dimensional description of the probability density for a given wave function.

  • NOTE: Orbital ≠ Orbit

  • Characterized by a set of quantum numbers which determine orbital size, energy, shape and orientation

The four quantum numbers for each wave function,𝜓 = 𝑛, ℓ, 𝑚ℓ, 𝑚𝑠 are:

1. n = principal quantum number

2. ℓ = angular quantum number

3. 𝑚ℓ = magnetic quantum number

4. ms = spin quantum number (does not come from Schrondinger )

The Principal Quantum Number:

• Describes average size of the orbital and indicates the energy level

• n can take on values of 1,2,3,4,5… (only be positive integers and can’t be 0)

• Same n initially defined by Bohr!

• The numbers also correspond to letters where 1 = K, 2 = L, 3 = M, 4 = N, etc.

• In a hydrogen atom, the energy of an electron with principal quantum number n is 𝐄𝐧= −𝟐. 𝟏𝟖 × 𝟏𝟎−𝟏𝟖 𝐉 (𝟏/𝐧^𝟐)

ψ2 gives probability of finding an electron in a given location:

“n” determines the size of this 90% boundary

The Angular Momentum Quantum Number, ℓ

• The shape of the boundary described by n is determine by angular momentum quantum number, ℓ (i.e the shape of the orbital)

• may take Integer values of ℓ = 0, 1, 2, 3,…n-1

• Note that n limits ℓ: l = n-1

• For example, if n = 1, ℓ can only be equal to 0

The value of ℓ also corresponds to a letter

• ℓ = 0 → s - corresponds to an s orbital (sphere/sharp)

• ℓ = 1 → p – corresponds to a p orbital(peanut/principle)

• ℓ = 2 → d – corresponds to a d orbital(double peanut/ diffuse)

• ℓ = 3 → f - corresponds to an f orbital( fancy/fundemental)

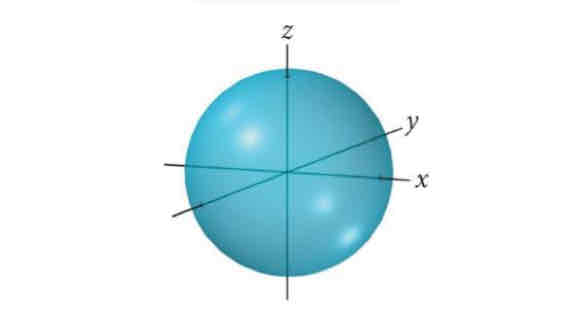
S-type l orbital

Spherical

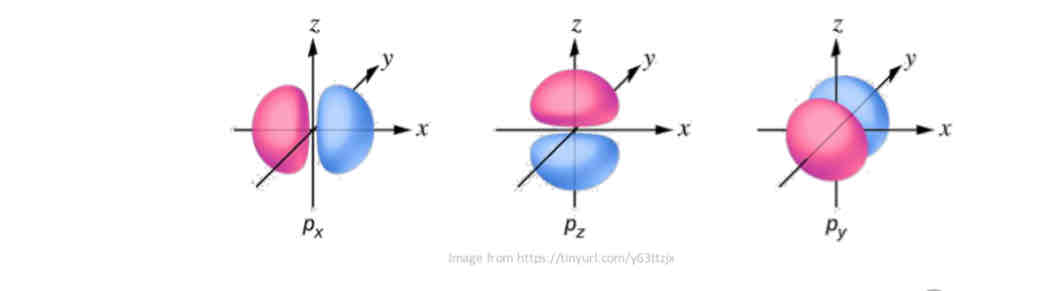
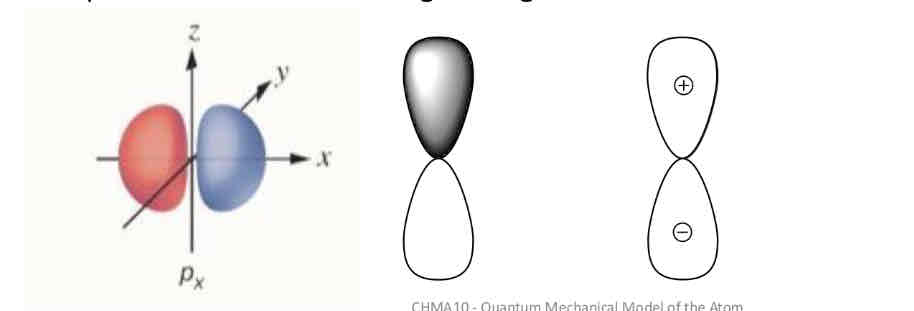
P-type l orbital :

• has a barbell shaped electron cloud and is centered at the nucleus.

• Why are p-orbitals represented with different colours?

  • The lobes of orbitals other than s orbitals are shaded differently to indicate the different phases of the wave function (more details to come…)

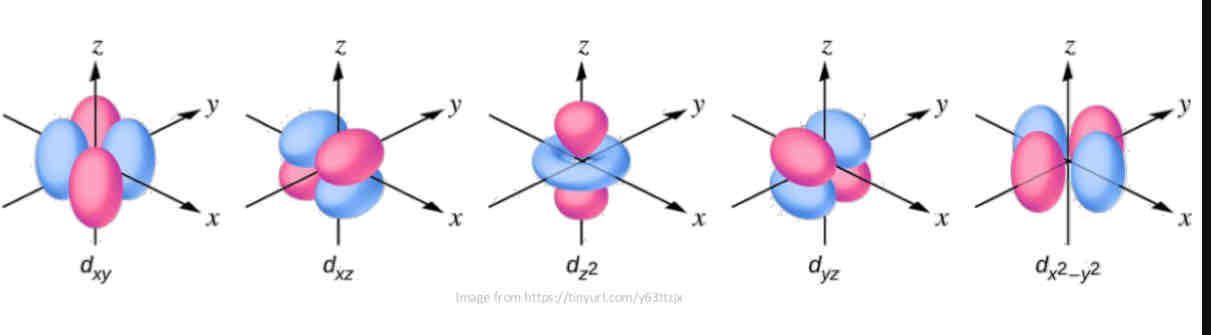
D-type l orbital

has a multi lobed shape and can have several lobes in a plane centered at nucleus

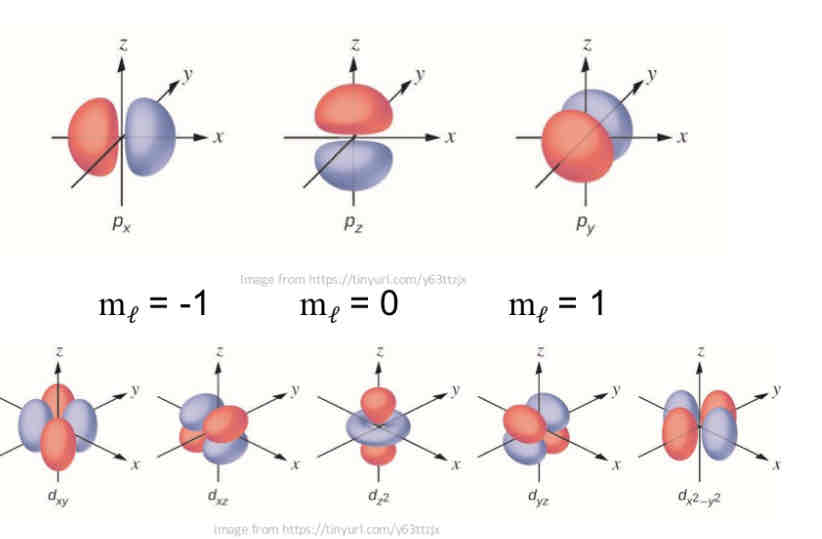
mℓ – The Magnetic Quantum Number

• The magnetic quantum number, mℓ , defines the spatial orientation of a single atomic orbital in space around the nucleus

• mℓ takes all integral values from –ℓ through 0 up to and including +ℓ

• mℓ = ( - ℓ…,0, …+ℓ)

• Note that ℓ limits mℓ: that is, angular momentum quantum number puts a limit on the magnetic quantum number

• For example, when ℓ = 1, that designates the p sublevel and there are only 3 allowable values of mℓ: - 1, 0 and + 1

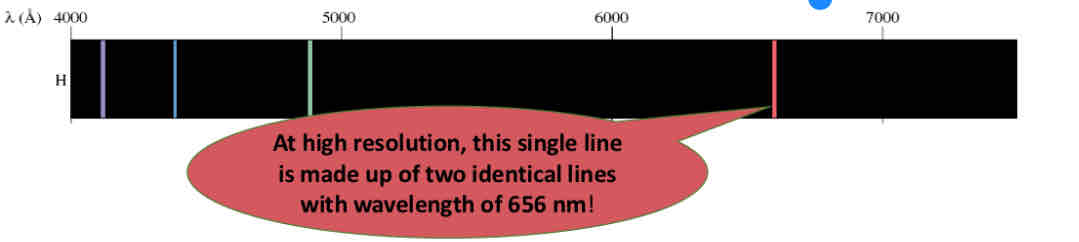
Atomic Spectra: Splitting of the lines

• atomic emission spectra appear as single lines, but this is not always the case!

• Using high resolution instruments reveals the lines can be made of multiple “split lines”of the same wavelength

• quantum mechanics had no explanation for this until, in 1925, Samuel Goudsmit and George Uhlenbeck suggested electrons have spin, and can be either “spin up” or “spin down”

• They proposed a fourth quantum number, ms, spin of the electron, that can take values of ½ or -½ to represent the two spin states of the electron

ml orbitals according to l number

• 1 s orbital

• 3p orbitals

• 5 d orbitals

• 7 f orbitals

Pauli

• It would take yet another student of Max Born named Wolfgang Pauli to add one of the final key tenets of modern quantum mechanics

• In 1925, using the ideas of Goudsmit and Ulenbeck, Pauli proposed that for a multielectron system (atoms other than hydrogen) there must be restrictions on the electrons in the orbitals

The Pauli Exclusion Principle states :

• that no two electrons in a poly-electron atom can be described by the same 4 quantum numbers

  • Two cats could not share same room, 2 humans can’t have same SIN number

  • No two electrons can have same address

ms - The Spin Quantum Number

• Every electron in an atom needs 4 quantum numbers to fully describe it

• Fourth quantum number

• Each orbital (s, p, d or f) can contain a maximum of 2 electrons so how can you tell the electrons in an orbital apart?

• We say electrons have a spin that can take values of ms = ± ½

• the value of ms also refers to the orientation of the magnetic field produced by the spin of that electron

• The concept of electron spin is a direct result of the Pauli Exclusion Principle

Orbital Nodes:

• region in space with zero probability of finding an electron

  • Result of destructive interference

2 types of Orbital Nodes:

• Angular

• Radial

Angular (planar or conical ) orbitals :

• Based off of l number

• never occurs in s orbitals becasue the s means the l=0

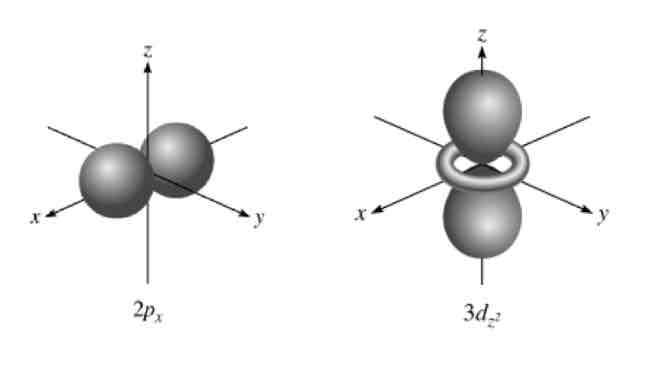
Radial (spherical) orbitals :

• Seen in radial distribution diagram

• Number of radial nodes = n-l-1

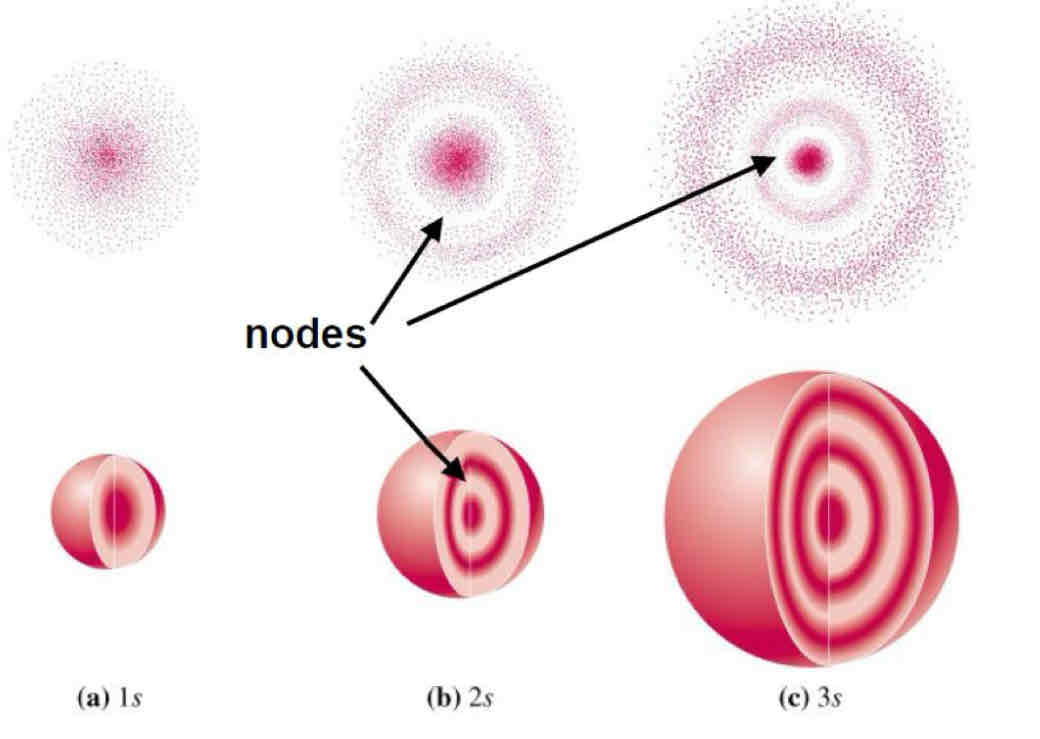
total number of nodes for any given orbital equals:

n-1

Orbital Phases

Wave functions (and therefore orbitals) have a phase

Orbitals change phase when:

• they cross a node

  • Represent with colour or sign change

Putting it all together

Quantum Field Theory: Paul Dirac

• By the end of 1925, both Heisenberg and Schrödinger’s mathematic models of quantum mechanics were published and on the way to being accepted by the scientific community

• At the same time, working alone, Paul M. Dirac (1902-

1984. developed his own version of quantum mechanics that brought together the idea of wave mechanics and matrix mechanics in one unified formulation now known as Quantum Field Theory

• Allowed light or electrons to be treated as a wave or a particle and gave results consisted with experimental data!

By 1927, all of these great scientists met to discuss and validate the new understanding of the subatomic:

• quantum mechanics

• at no other point in history have we seen so many great minds gathered in one place to usher in a new era of scientific understanding

Orbital Energies in a Hydrogen Atom

• Energy depends only on principal quantum number

  • Only one electron

Multi-Electron Systems

• Schrodinger’s equation can only be solved exactly for a one-electron system.

• Multi-electron systems are complicated by electron-electron repulsion.

• Can approximate a solution for many-electron systems by assuming “hydrogen-like” orbit

• Orbital energies depends on n and l

Why Do Orbital Energies Split?

We can look to Coulomb’s Law to help explain why orbitals lose degeneracy! 𝐸𝑝𝑜𝑡 =(1/4𝜋𝜀𝑜)(𝑞1𝑞2/𝑟)

Attraction and repulsion of two charged particles influenced by:

1. Charge on particles • energy is positive for same charge leading to repulsion i.e less stable • energy is negative for opposite charges leading to attraction i.e. more stable

2. The distance between the particles • Closer together, the greater the energy • These ideas are the basis for explaining periodic trends of the elements

Electron Shielding

• Atom composed of protons and electrons (neutrons too…but they have no charge!)

• with more than one electron present, have both attractive (electron-proton) and repulsive (electron-electron) interactions

• Electrons screen or shield each other from the full force of the nuclear charge (where the protons live)

• Electrons closer to the nucleus (in lower energy levels) are more effective at shielding than electrons farther from the nucleus (Coulomb’s Law)

• Leads to some orbitals being more stable than others

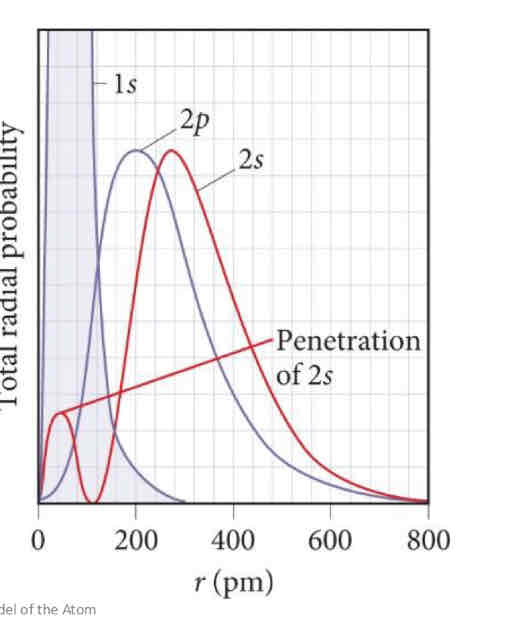
Electron Penetration

• From radial distribution function, we see that the s and p functions overlap

• What does this overlap mean?

  • Compare the 1s and 2s functions…we see there is a local maximum from the 2s within the 1s function

  • This indicates that there is a high probability of finding the 2s electron close to the nucleus i.e. the 2s electrons penetrate the 1s orbital

  • 2p orbital does not have a local maximum and hence 2p electrons do not penetrate to the nucleus as effectively as 2s electrons!

Electron configuration

is distribution of an atom’s electrons among its atomic orbitals

orbital diagrams:

H ↑

spdf notation:

1s^ 1

Multi electron atoms require rules

Aufbau Principle and Hund’s Rule

The Aufbau principle

• tells us the order we need to use to fill in electrons

  • Important to note that this order applies only to atoms and ions not bonded to anything else!

  • Electrons will occupy the lowest energy orbitals first

  • They will enter higher orbitals only when the lower energy orbitals are filled.

  • order: 1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s

Aufbau Chart

Hund’s Rule: Energy Levels of Orbitals

• When we are writing electron configurations for atoms, it is important to remember that not all orbitals have the same energy

• In fact, orbital energy increases with increasing value of n

• when orbitals have equal energy, we call them degenerate

• If there are degenerate orbitals, the electron configuration of lowest energy has the maximum number of unpaired electrons with parallel spins

• For example, when filling degenerate orbitals, electrons fill them singly first, with parallel spins

• When 2 electrons occupy separate orbitals of equal energy, the repulsive interaction between them is lower

• Hence repulsive forces are minimized because the electrons are spread out over a larger region of space • This leads to a more stable configuration

Hunds Rule Example

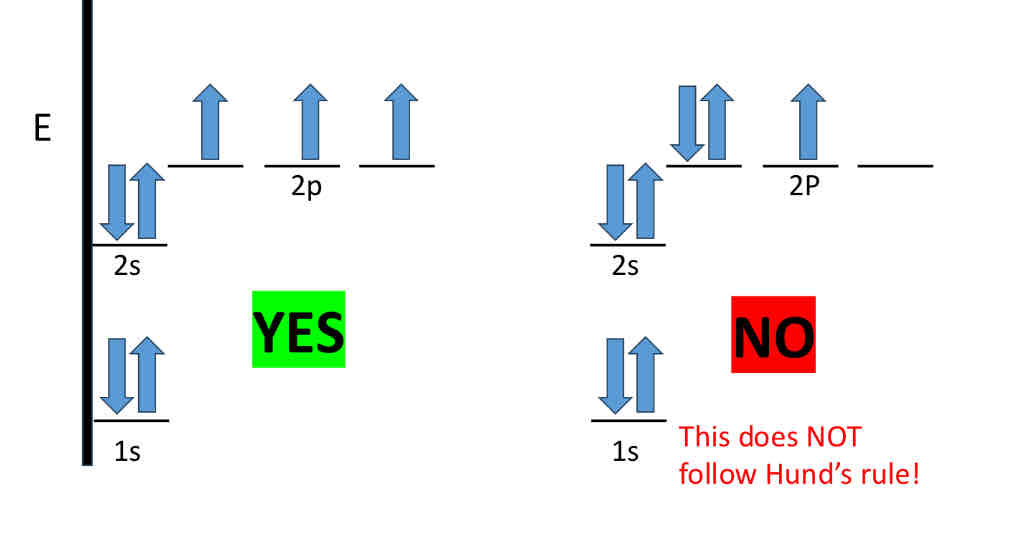
Does Electron repulsion has any effect on spin

no

Electron Configurations: Getting To Heavier Elements

• For the first 10 or so elements, we can easily write down all of the orbitals that are occupied by electrons

• As we start to fill more and more orbitals (i.e. when the atoms have 50 or 60 electrons), it becomes tedious to write the core electron configuration

• We can use the electron configuration of a Nobel gas to represent the core of electrons

• For example, Na has 11 electrons and is in the 3rd row

• Since neon is right before Na, we can write [Ne]3s1 for the electron configuration of Na rather than 1s^2, 2s^2, 2p^6, 3s^1

Orbital Filling for Transition Metals

• The transition metals start in the fourth row

• All of these elements have argon as a core electron structure: [Ar] = 1s^2,2s^2,2p^6,3s^2,3p^6

• Start around Z=19

Radon

• radioactive

• breathing it in (common where there are rocks -north Ontario) can lead to lung cancer

Copper

• is [Ar]4s^1,3d^10and not [Ar]4s^2,3d^9, as would be expected from the Aufbau principle.

• The loss of the electron from the 4s orbital completes the 3d sub-orbital and leaves it in a more stable, lower energy state.

• This lowest energy electron configuration is determined by the electron-pairing energy and the exchange energy. The two electrons in the 4s orbital will repel each other slightly, and this will cause a minor increase in the energy of the atom.

• The removal of one of the electrons from the 4s shell will remove this energy increase which is caused by the pairing energy.

• When electrons can exchange between orbitals, the energy of the atom is lowered.

• This electron exchange can occur when there are degenerate electron configurations, and the electrons of the same spin can exchange between orbitals

Manganese

the same is true for manganese. It’s ground state is [ Ar ] 3 d ^5, 4 s^ 2

Orbital Filling for Transition Metals

• The energy of the 4s and 3d orbitals is very similar

• Recall that s and p orbitals penetrate towards the nucleus more efficiently than d or f orbitals

• This lowers the energy of electrons in the 4s since they spend more time near the nucleus!

• Chromium (which is the 6th transition metal and hence has 6 electrons to put in its outermost orbitals) is an exception because extra stability is gained when an orbital is half filled

• Why? This avoids pairing electrons in the same orbitals so repulsions are minimized

Orbital Filling for Transition Metals copper

• Copper is also an exception due to the energy of the 4s and 3d orbitals being very similar

• It turns out that having all five of the 3d orbitals filled and a half full 4s orbital is more stable than having 4 and a half filled 3d orbitals and a full 4s!

• Electron configurations for the 4d and 5d metals is more complicated