AP Calc Exam

Removable discontinuity

Point discontinuity: limits are approaching the same value, but there is a hole at that point and the function value is in a different location

Non-removable discontinuity

Infinite discontinuity: limits are forever approaching different values

Jump discontinuity: one limit approaches a hole, the other approaches the function value from above or below the hole

MVT theorem (derivatives)

MVT theorem (integrals)

EVT theorem

IVT theorem

When is ‘+C’ included

Include ‘+C’ when integrating a function that does not have limits (the a and b values that are plugged in after integration)

How is continuity evaluated

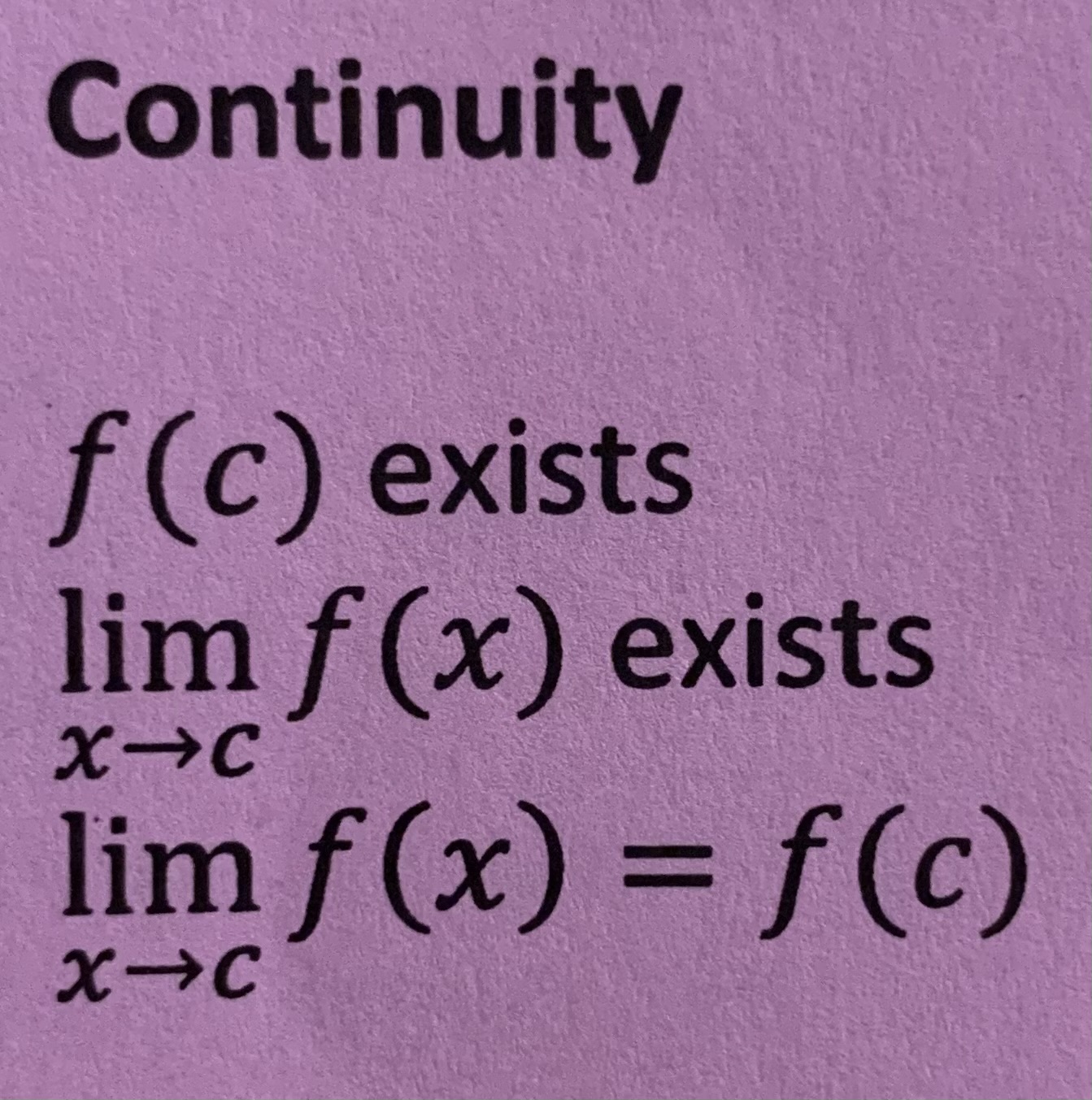
Area of semicircle cross sections formula

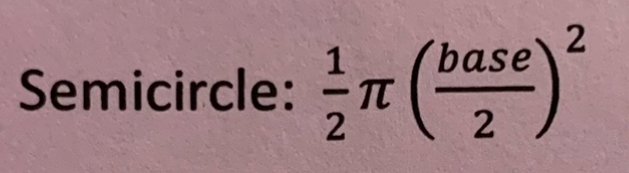
Area of equilateral triangle cross sections formula

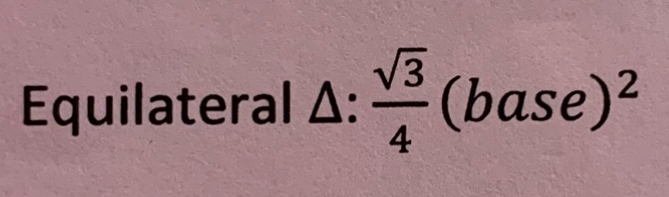
Area of isosceles right triangle cross sections formula

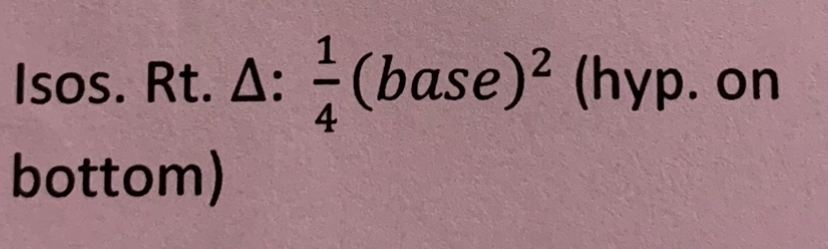
Finding the area between 2 curves:

Finding the volume of a disk or washer:

Finding the volume of a shape with cross sections:

Completing the square

1) trinomial equation

2) take b, divide by 2 and square

3) slide c over, put in the number from step 2, and undo the number from step 2

Example: x²+12x+32 → x²+12x+36-36+32

4) separate the first 3 terms from the last two and factor the trinomial, combine the other two numbers

Example: x²+12x+36-36+32 → (x+6)² -4

5) set equal to zero and solve

RRAM formula

Difference between x₀ and x₁, multiply that by the y value at the right-hand value, in this case the y value at x₁

LRAM formula

Difference between x₀ and x₁, multiply that by the y value at the left-hand value, in this case the y value at x₀

MRAM formula

Take the value of each interval (b-a) and multiply that by the fist x value (x₀) plus the second x value (x₁) divided by 2

Example: b[f((x+x)/2)+ …]

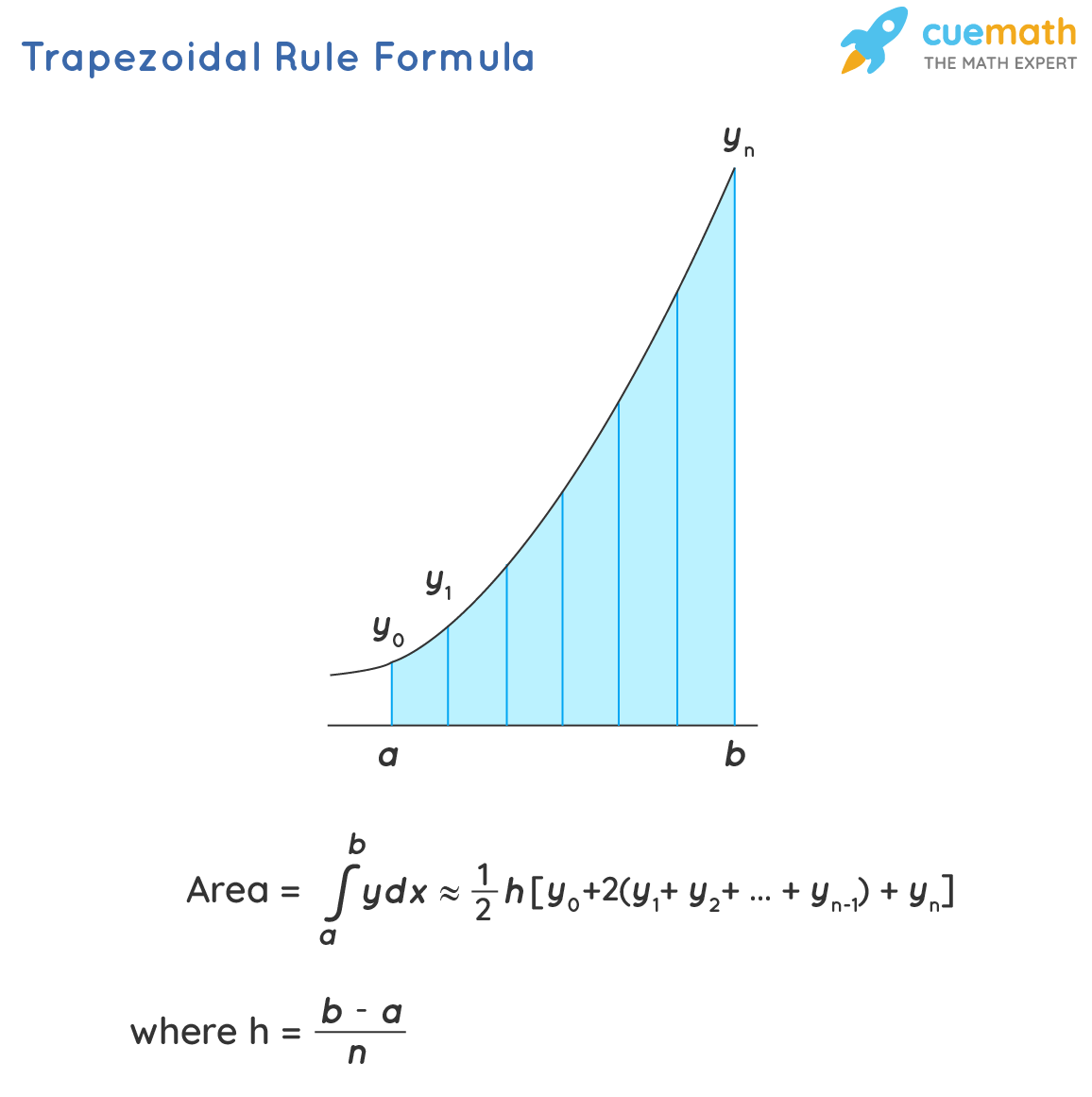
TRAP formula

Basic trig derivatives

Sin(x)= cos(x)

Cos(x)= -sin(x)

Tan(x)= sec²x

Csc(x)= -csc(x)cot(x)

Sec(x)= sec(x)tan(x)

Cot(x)= -csc²x

AROC

(X₁,X₂) (Y₁, Y₂) → (Y₂-Y₁)/(X₂-X₁)

Basically, AROC is the average velocity over a short period of time.

IROC

IROC is the more specific version of AROC. Find the AROC of the values leading up to the value you are looking for the IROC at, and the value that those are approaching will tell the specific point that is being solved for.