Maths Partie B

Studying for Alberta math part PAT

✅ Réponse correcte : C. 0,9

Car ce n’est pas un carré parfait.

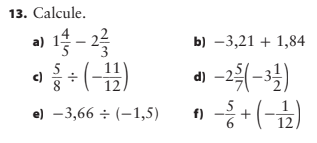
a) 1 4/5 - 2 2/3 = -13/15
b) -3.21 + 1.84 = -1.37
c) 5/8 ÷ (-11/12) = -15/22
d) -2 5/7 × (-3 1/2) = 9 1/2
e) -3.66 ÷ (-1.5) = 2.44
f) -5/6 + (-1/12) = -11/12

✅ Réponse : A. (-7)^6

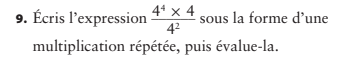
✅ Réponse finale : 64

a) (4a + 3 + 9a + 1)
Regroupons les termes avec « a » et les constantes :
→ (4a + 9a = 13a)
→ (3 + 1 = 4)
Résultat : (13a + 4)

b) (2b² - 5b - 4b² + 8b)
Regroupons les termes en (b²) et en (b) :
→ (2b² - 4b² = -2b²)
→ (-5b + 8b = 3b)
Résultat : (-2b² + 3b)

c) (1 - c + 4 + 2c - 3 + 6c)
Additionnons les constantes et les termes en (c) :
→ (1 + 4 - 3 = 2)
→ (-c + 2c + 6c = 7c)
Résultat : (7c + 2)

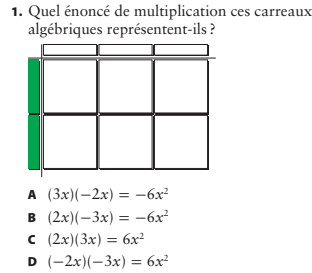
✅ La bonne réponse est : B. (2x)(-3x) = -6x²

✅ Résultat final : (8,1y^2)

La bonne réponse est D. 8,1y² 🎯

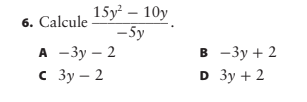
✅ La bonne réponse est : B. (-3y + 2)

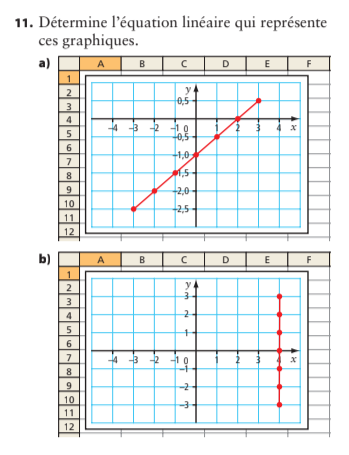
Équation de la droite passant par (–4, –3) et (4, 3)
✅ y = (3x) ÷ 4
ou sous forme équivalente : 4y = 3x

b) Droite verticale
✅ x = 2

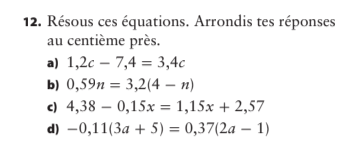
a) (1,2c - 7,4 = 3,4c)

Soustrayons (1,2c) des deux côtés :
(-7,4 = 2,2c)

Puis divisons :
(c = -7,4 ÷ 2,2 ≈ ) –3,36 ✅

b) (0,59n = 3,2(4 - n))

Développons le membre de droite :
(0,59n = 12,8 - 3,2n)

Ajoutons (3,2n) :
(3,79n = 12,8)

Divisons :
(n = 12,8 ÷ 3,79 ≈) 3,38 ✅

c) (4,38 - 0,15x = 1,15x + 2,57)

Soustrayons (1,15x) des deux côtés :
(4,38 - 1,3x = 2,57)

Soustrayons 4,38 :
(-1,3x = 2,57 - 4,38 = -1,81)

Divisons :
(x = -1,81 ÷ -1,3 ≈) 1,39 ✅

d) (-0,11(3a + 5) = 0,37(2a - 1))

Développons chaque côté :
(-0,33a - 0,55 = 0,74a - 0,37)

Regroupons les termes :
(-0,33a - 0,74a = -0,37 + 0,55)
(-1,07a = 0,18)

Divisons :
(a = 0,18 ÷ -1,07 ≈) –0,17 ✅

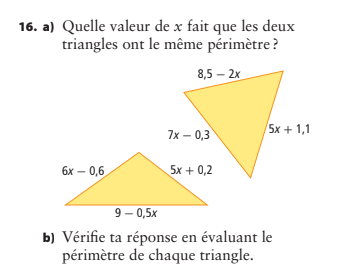
🔹 Étape 1 — Calcule des périmètres :

Premier triangle :
(P_1 = (6x - 0,6) + (5x + 0,2) + (9 - 0,5x))
→ Regroupons les termes :
(6x + 5x - 0,5x = 10,5x)
(-0,6 + 0,2 + 9 = 8,6)
➡ Périmètre 1 = 10,5x + 8,6

Deuxième triangle :
(P_2 = (8,5 - 2x) + (7x - 0{,}3) + (5x + 1,1))
→ Regroupons :
(-2x + 7x + 5x = 10x)
(8,5 - 0,3 + 1,1 = 9,3)
➡ Périmètre 2 = 10x + 9,3

🔹 Étape 2 — Égalité des périmètres :

[ 10,5x + 8,6 = 10x + 9,3 ]

Soustrayons (10x) des deux côtés :
[ 0,5x + 8,6 = 9,3 ]

Soustrayons 8,6 :
[ 0,5x = 0,7 ]

Divisons :
[ x = 0,7 ÷ 0,5 = 1,4 ]
✅ Valeur de (x) : 1,4

🔹 Étape 3 — Vérification :

Périmètre 1 :
(10,5 × 1,4 + 8,6 = 14,7 + 8,6 = 23,3)

Périmètre 2 :
(10 × 1,4 + 9,3 = 14 + 9,3 = 23,3)

✅ Les deux périmètres sont égaux : 23,3

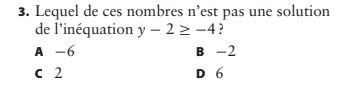
➡ Réponse correcte : A. –6

Tu veux une autre question rapide dans le même genre ? 😄✍

Étape 1 — Développons le côté gauche :
(5x - 15 ≤ 2x + 3)

Étape 2 — Regroupons les termes :
(5x - 2x ≤ 3 + 15)
(3x ≤ 18)

Étape 3 — Divisons :
(x ≤ 6)

✅ Réponse : C. x ≤ 6

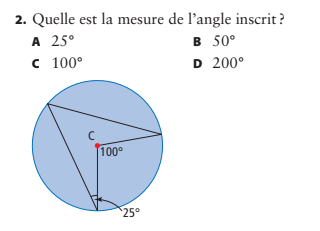
On utilise la règle suivante :
✅ Un angle inscrit intercepte un arc deux fois plus grand que lui, donc il mesure la moitié de l’angle au centre.

[ \text{Mesure de l’angle inscrit} = 100° ÷ 2 = 50° ]

✅ Réponse correcte : B. 50°

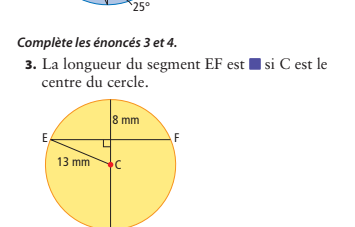
√(13² − 8²) = √(169 − 64) = √105 ≈ 10,25
EF = 2 × 10,25 = 20,5 mm ✅

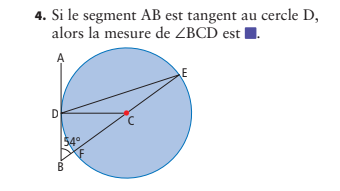
Lorsque une tangente et un rayon se rencontrent, l’angle entre eux est 90°. Donc :
∠CBD = 90°

Dans le triangle ∆DBF, on a :
∠CBD = 90° et ∠DBF = 54°

Comme la somme des angles d’un triangle est 180° :
∠BDC = 180° − 90° − 54° = 36°

✅ Réponse : 36°

Formule : Aire de la surface (sans couvercle) = π × r²
(Il s’agit de l’aire du disque supérieur)

🔹 Tasse bleue :
Diamètre = 8 cm → rayon = 4 cm
Aire = π × 4² = π × 16 ≈ 50,27 cm²

🔹 Tasse rouge :
Diamètre = 6,5 cm → rayon = 3,25 cm
Aire = π × 3,25² ≈ π × 10,56 ≈ 33,18 cm²

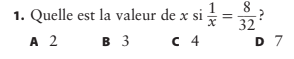
On te donne :
1/x = 8/32

—

Étape 1 — Simplifie 8/32 :
8 ÷ 32 = 1/4

Donc :
1/x = 1/4

Étape 2 — Inverse les deux côtés :
x = 4 ✅

—

Réponse : C. 4

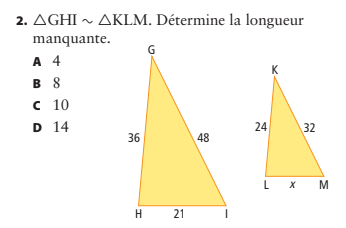
Les triangles ∆GHI et ∆KLM sont semblables, donc leurs côtés correspondants sont proportionnels.

On compare les côtés connus :

• GH = 36 et KL = 24 → rapport = 24 ÷ 36 = 2/3

• GI = 48 et KM = 32 → rapport = 32 ÷ 48 = 2/3

Donc, le rapport de similitude est 2/3.

On applique ce rapport à HI = 21 pour trouver LM :

[ LM = 21 × \frac{2}{3} = 14 ]

✅ Réponse : D. 14

Voyons pourquoi Louis et Matt obtiennent des résultats très différents en sondant des gens à propos de la même sculpture 🎭

Louis fait son sondage au centre commercial et Matt au centre des arts. Donc :

• Leurs publics cibles ont probablement des goûts, intérêts et perspectives culturelles différents → ✅ différences culturelles

• La langue utilisée n’a pas été mentionnée comme différente, donc ce facteur n’explique pas nécessairement leurs écarts → ❌

✅ Bonne réponse : A