Biophysics (Elasticity)

Elasticity definition

the property of an object to recover its original size and shape after removing the stretch force applied to it

An object that can' recover its original size is called

plastic

Definition of stress

T = F/A [N/m²]

Stress is the force applied by surface area. Units are Newtons by square meter

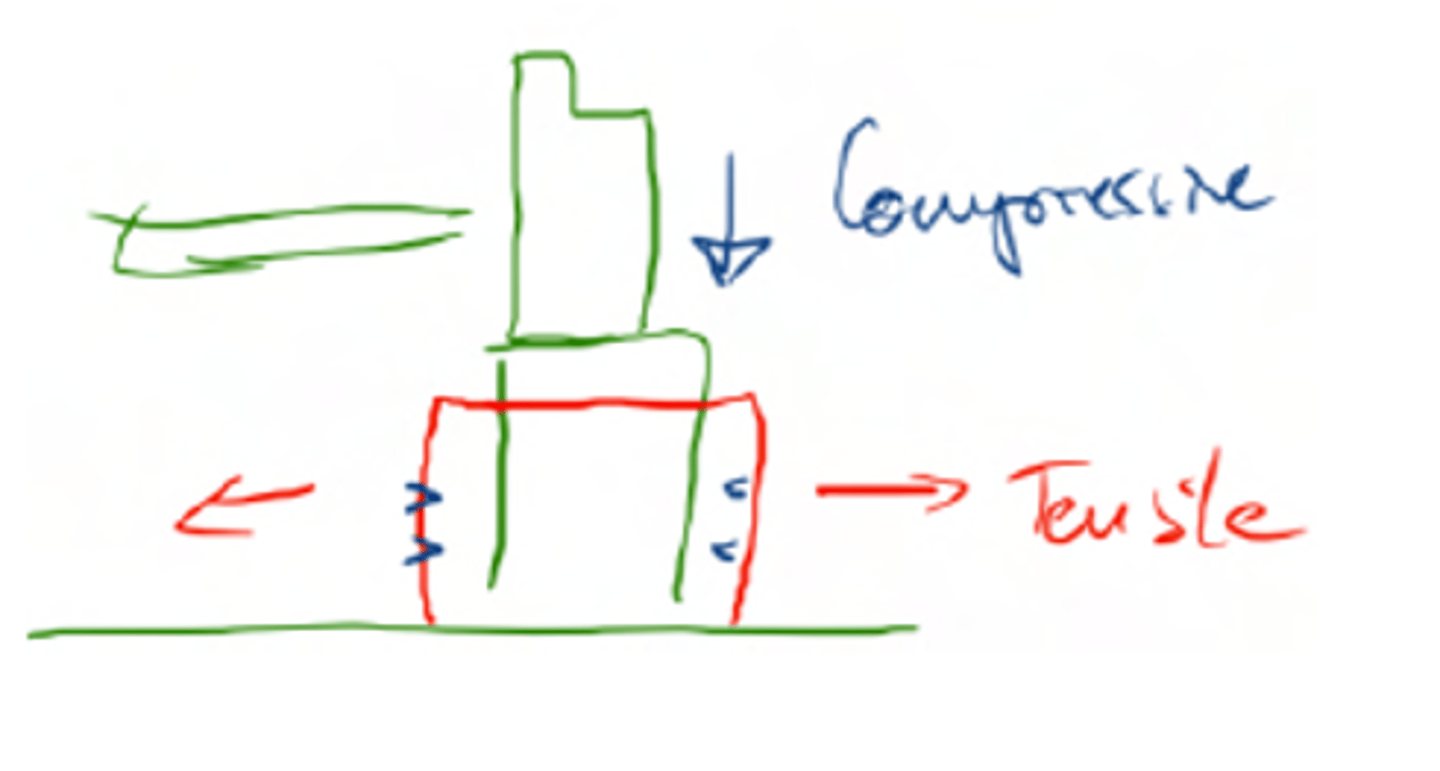
Longitudinal or normal stress

Force is applied perpendicular to the surface (cross-sectional area). This force can be tensile or compressive

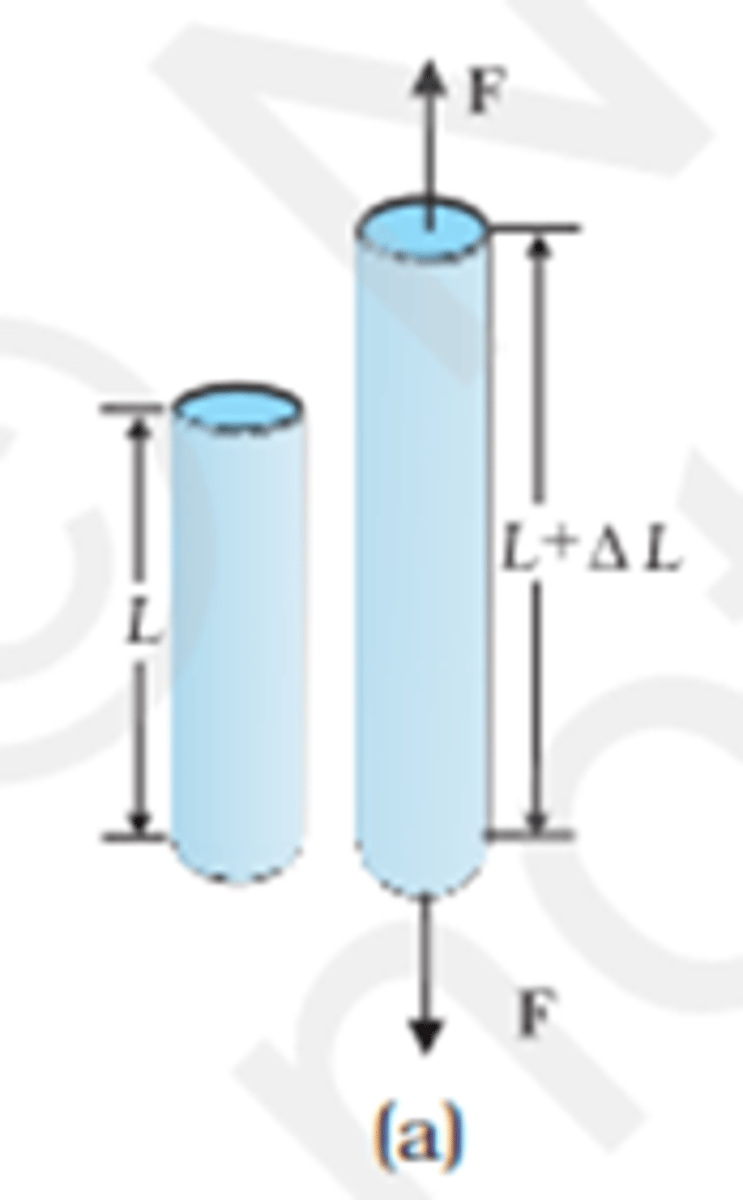
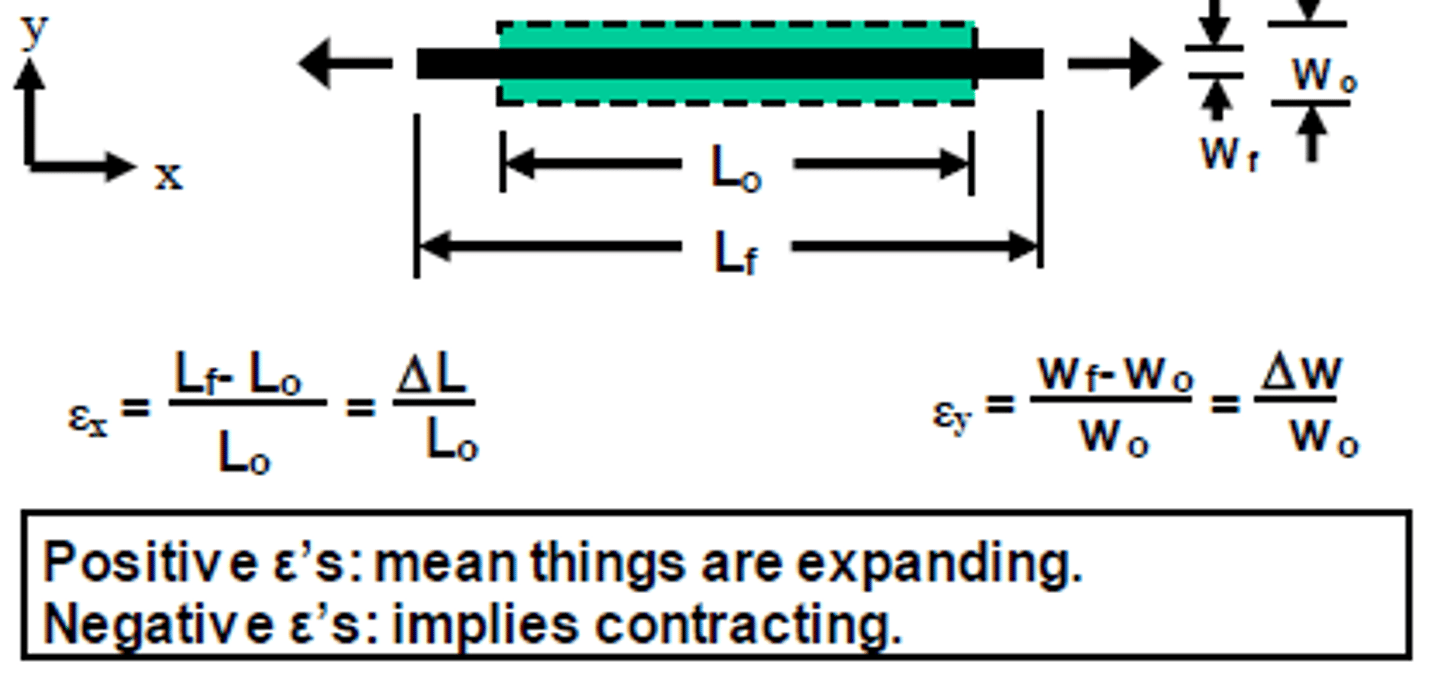
Longitudinal strain

∆L/L

Deformation by length unit. It is adimensional.

It is to measure or characterize deformation of materials with longitudinal strain

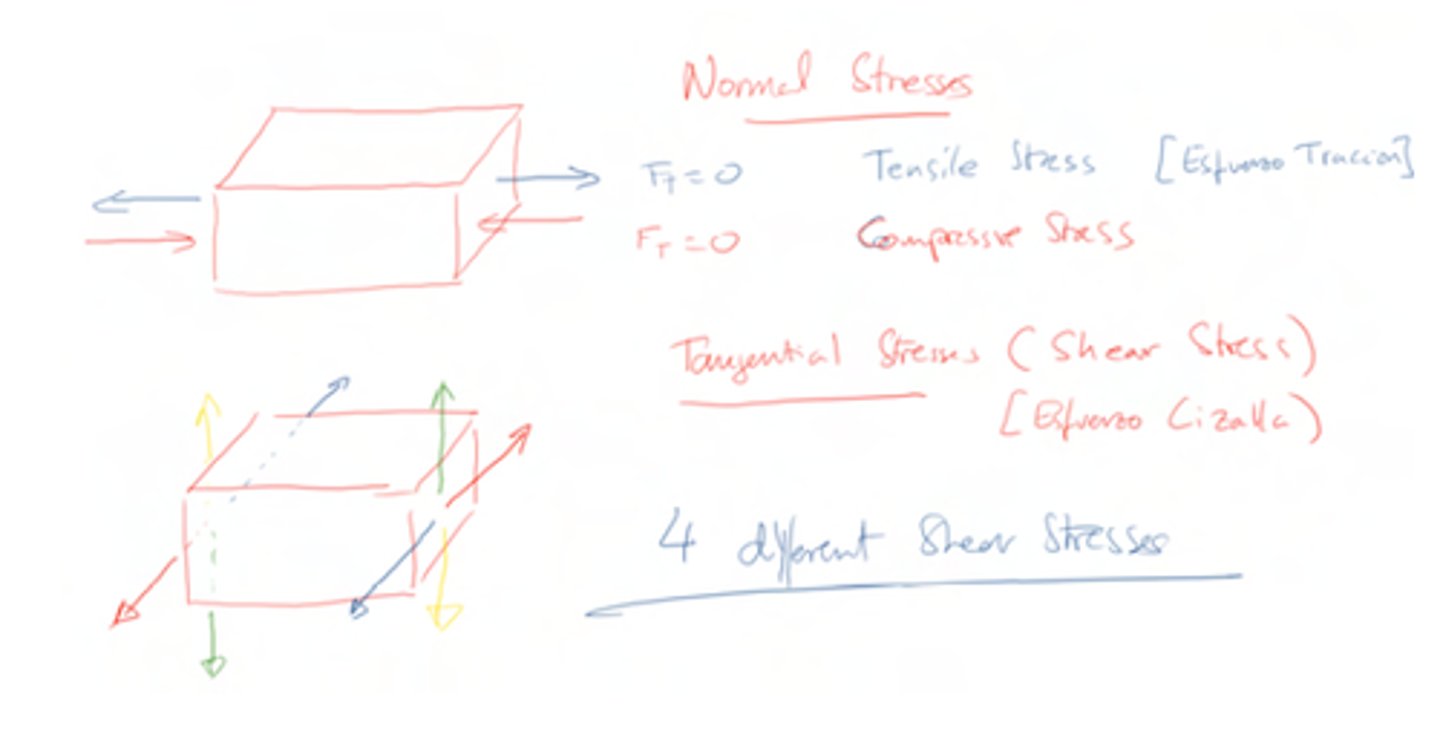
How many different stresses can happen in a solid?

6, 4 shear stress and 2 normal stress

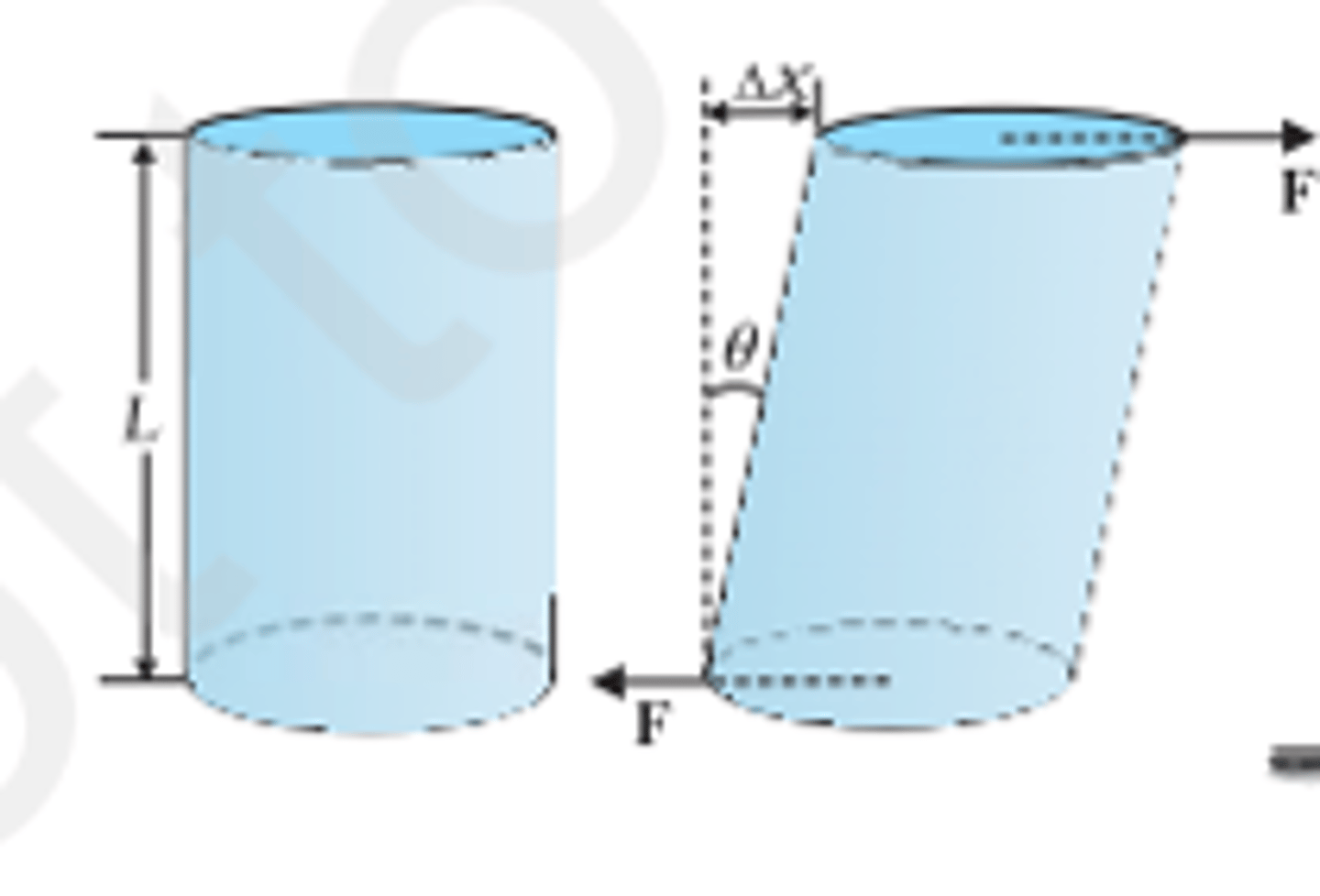
Shearing (Cizalla) or longitudinal strain

The force applied is parallel to the cross-sectional area

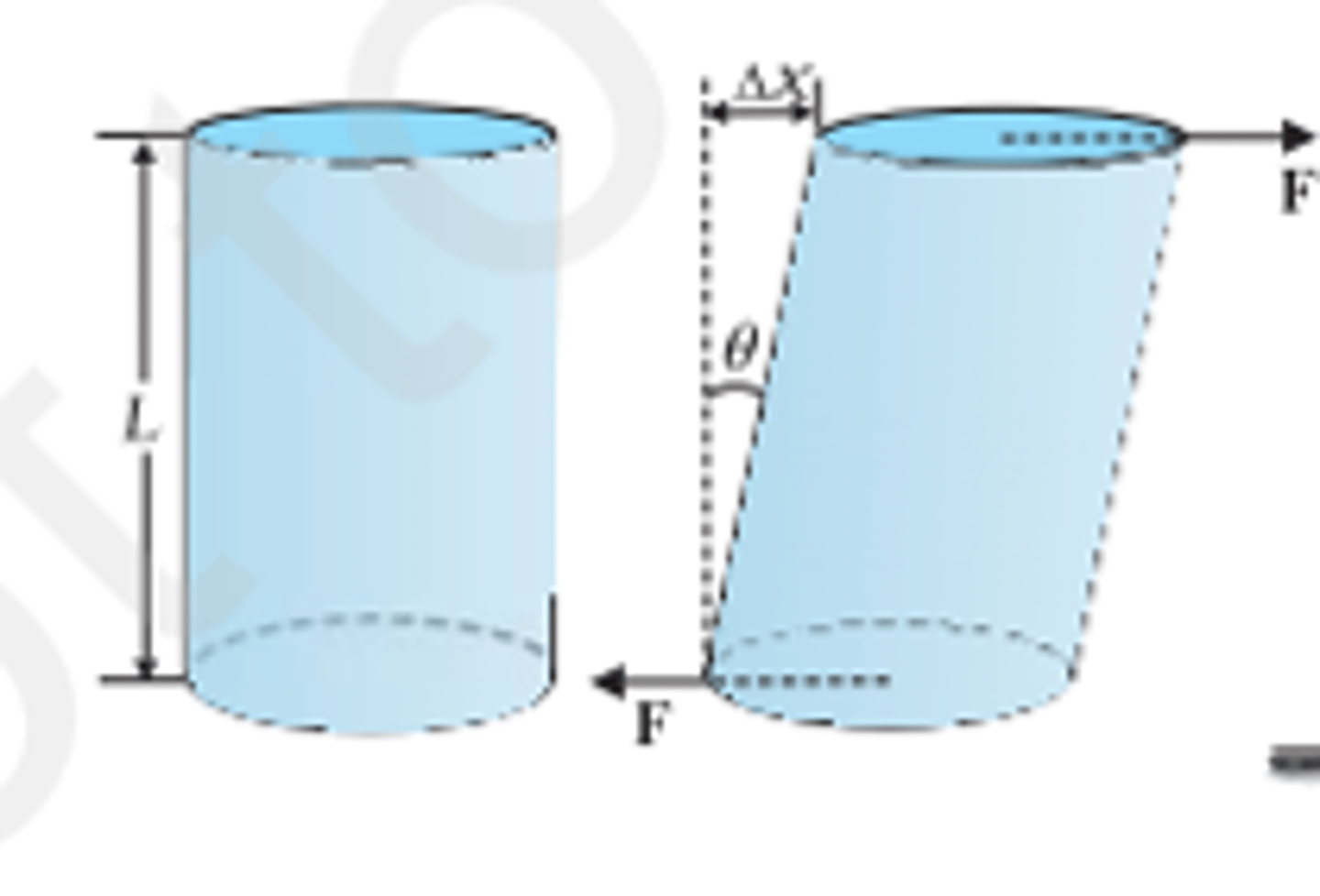
Shearing strain

Deformation applied by the force. It is used to measure deformation of materials with shearing strain

Shearing strain = ∆x/L = tan θ

Hooke's Law

F = -Kx (K= spring const)

The stress is proportional to the elongation

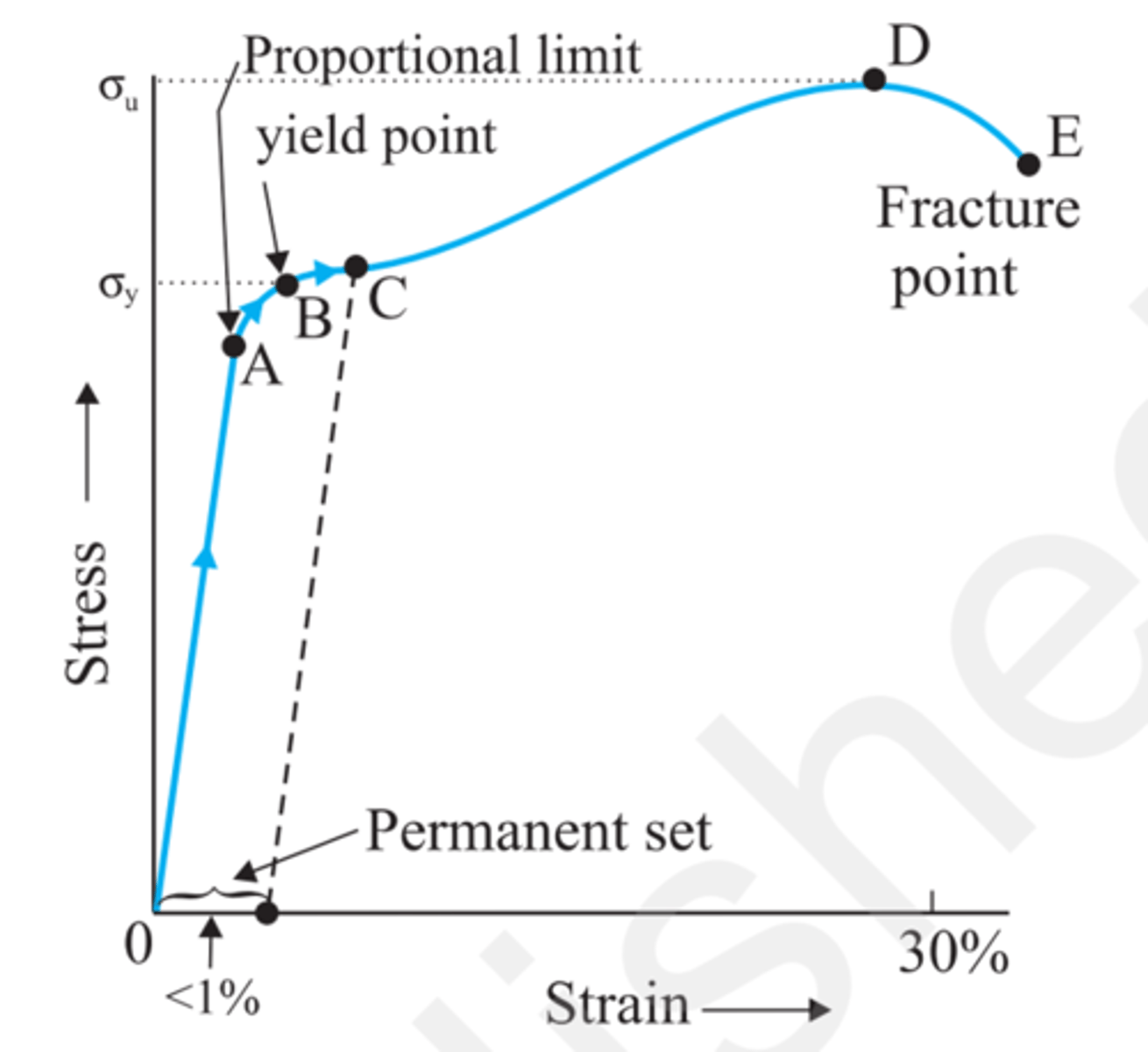
Stress Curve

From 0 to point A -> stress proportional to the elongation. It applies the Hooke's law. Stress and strain are proportional.

In this area the body is elastic. It will recover original size and shape

Stress Curve

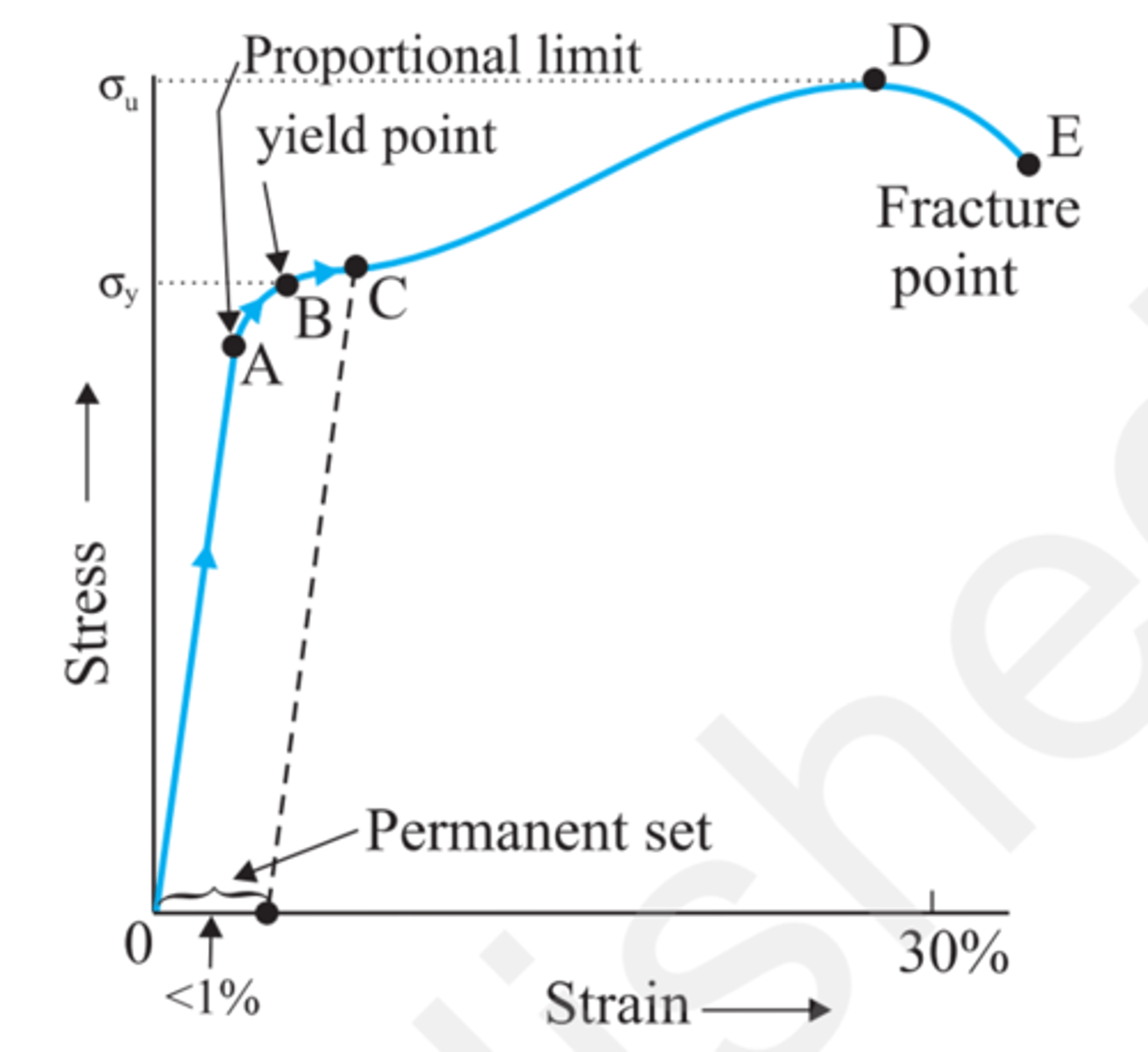
From A to point B -> stress is no longer proportional, but it is still elastic. it will recover original size and shape

Stress Curve

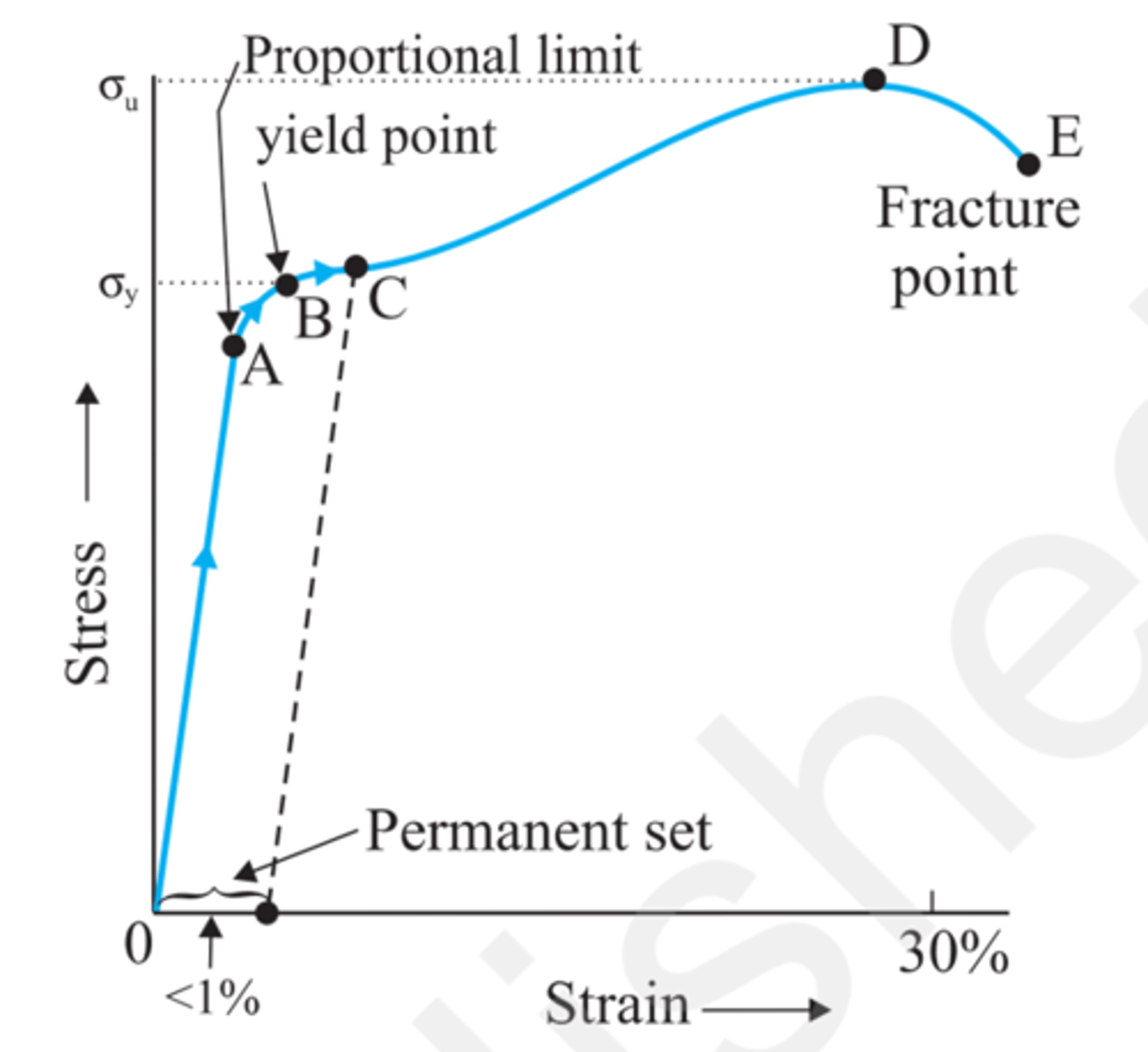
From point B to point D -> small stress produces big strain. The body is in plastic area. It will no recover the original size and shape

Stress Curve

From point D to point E -> even if stress is decreased there is still strain, until reach the breaking point

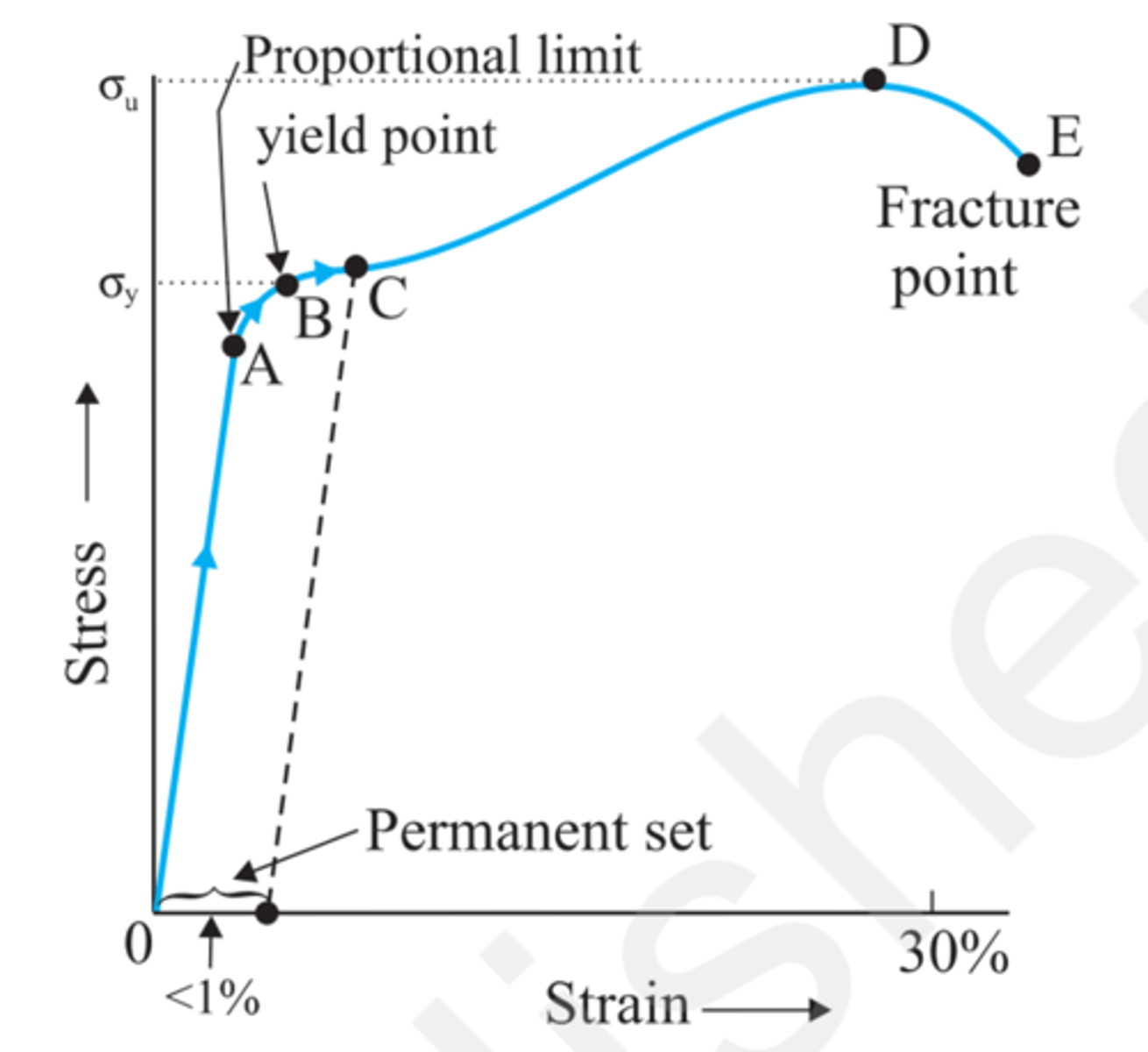
yield strength (σy)

Strength limit to reach the maximum elastic point. Strengths bigger than this the body will be in the plastic area and not recovering the elastic behaviour

At point B, we have the yield strength. The strain in this point is yield point of elastic limit

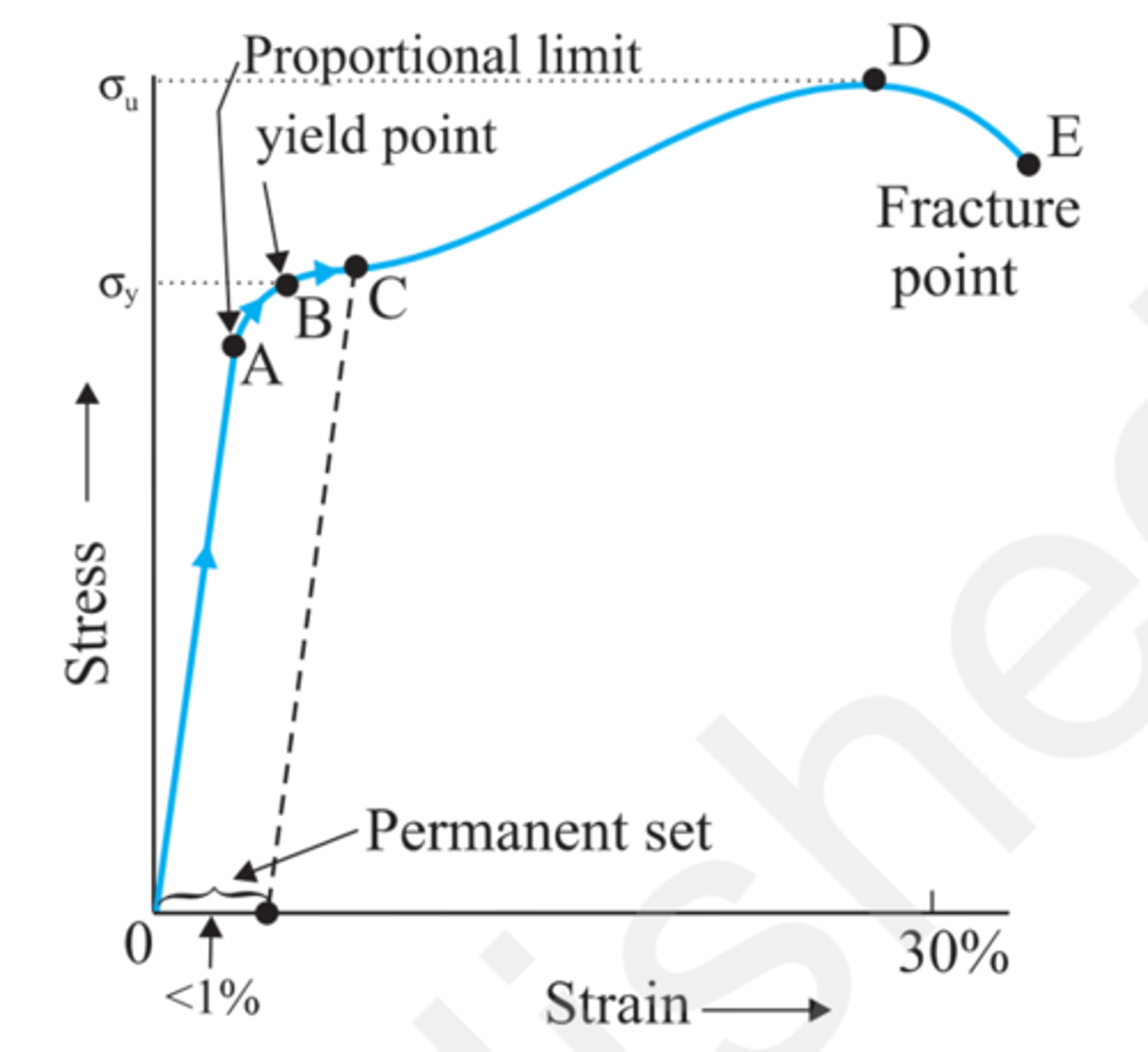
At point C we will achieve a permanent deformation of

1%

Parallel line to the elastic zone passing at point C

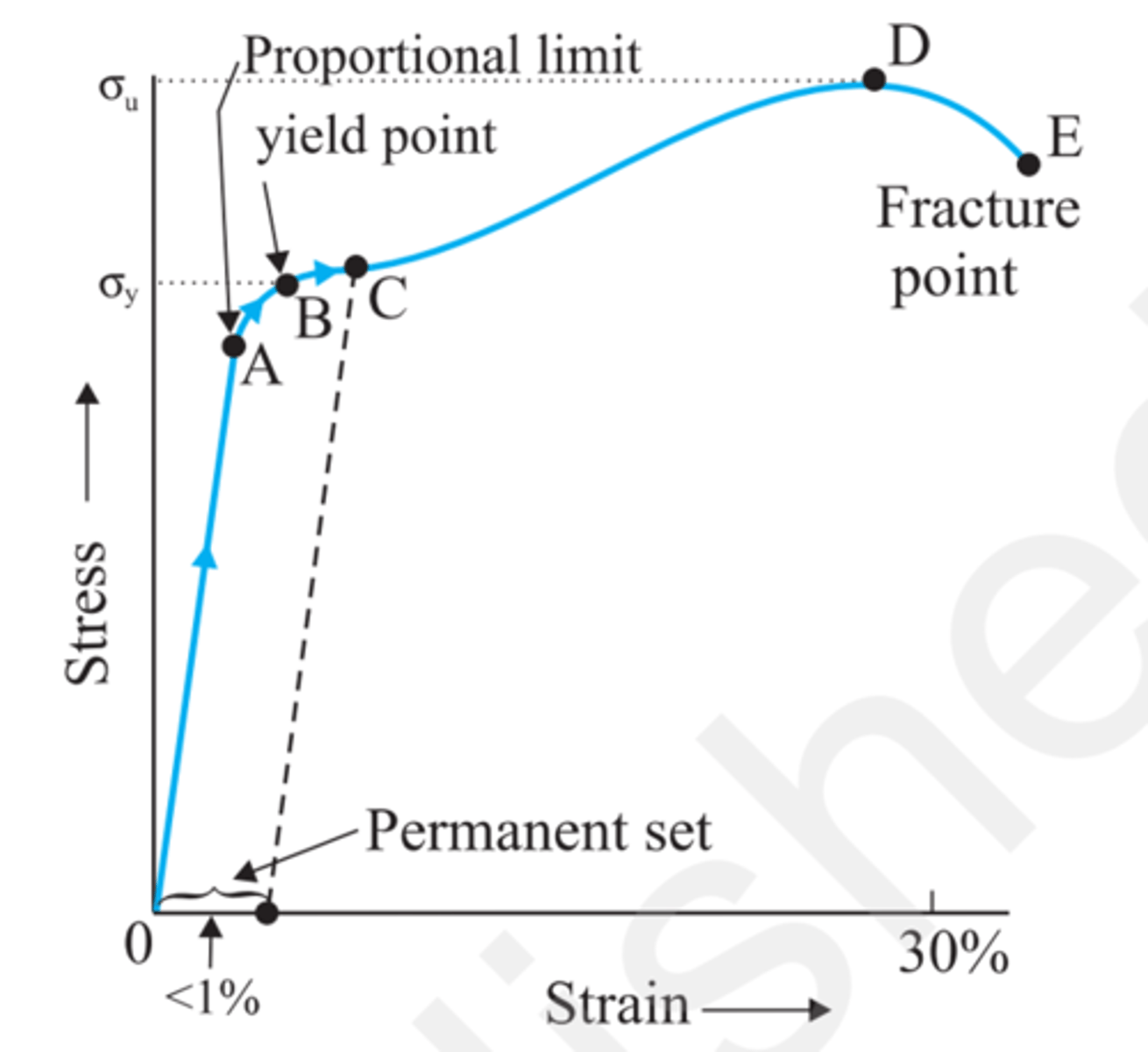
tensile strength (σu)

Strength limit in the plastic area.

Point D.

Strain is called tensile strength

Young's Modulus Stretching/Compression

The ratio of tensile (or compressive) stress (σ) to the longitudinal strain (ε)

It is measured in [N/m²]

Y = (F/A)/(∆L/L)

Young's Modulus is used to characterize elasticity of materials under longitudinal stress

Big Young's Modulus means that will be necessary a _____________ to produce a ______________ strain

big small

For an homogeneous and isotropic material, longitudinal and transversal Young's modulus are _______________

Equal

Order Young'' modulus of bones, ligaments and muscles

Bones > Ligaments > Muscles

Stress vs Young Modulus

T = Y (∆L/L)

Stress = Youngs' Module * (∆L/L)

Shear Modulus

The ratio of shearing stress to the corresponding shearing strain

G = (F/A)/(∆x/L)

G = σs/θ

σs= G θ

The shear modulus is used to characterize elasticity of materials under shear stress

Homogeneous Materials

The composition is the same in all the places

Isotropic Materials

The properties of the materials are the same in different directions

Brittle materials are having mainly

elastic zone. The crack point will be reach earlier

Characteristic of tensile stress on bones

. Properties along and across the axis are different (anisotropic)

. Stress and strain curves will be different for tensile or shear stress

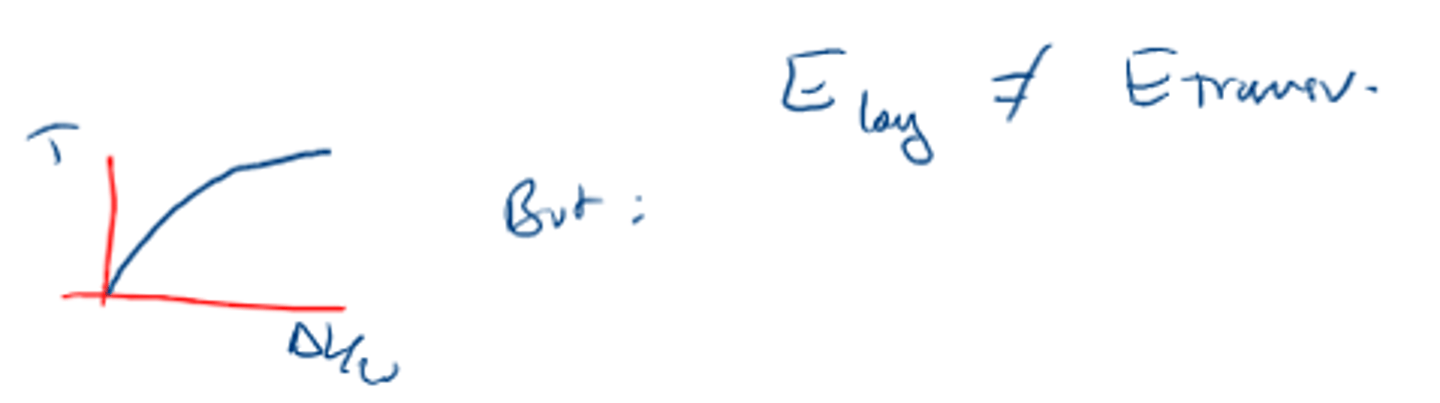
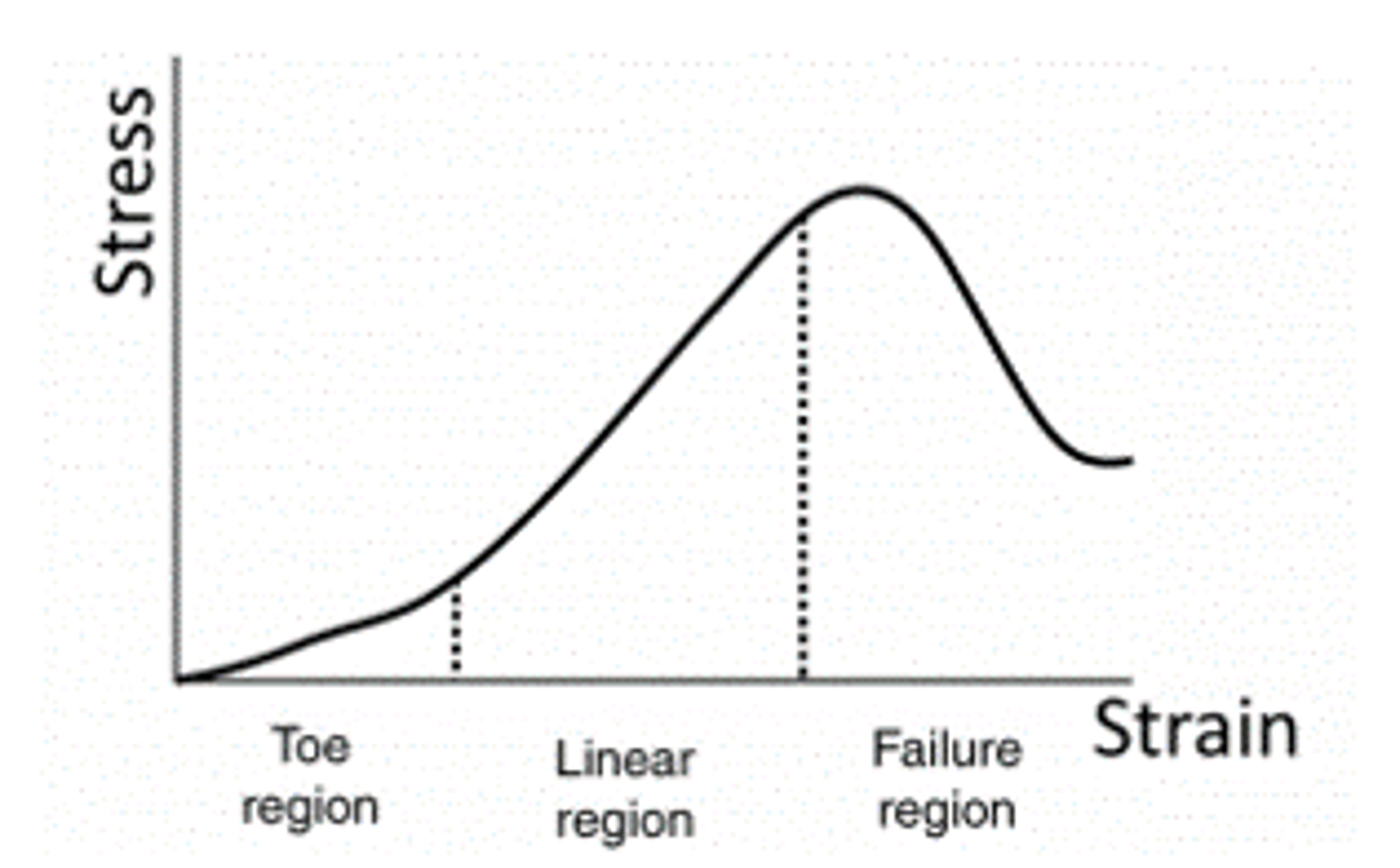
Characteristic of tensile stress on ligaments/tendons

Three main areas:

. Toe (Región basal) -> small stress provokes big strain. Fibers at rest are folded. In this area they move from fold to parallel.

. Elastic area -> Fibers are unfolded and strain and stress are proportional

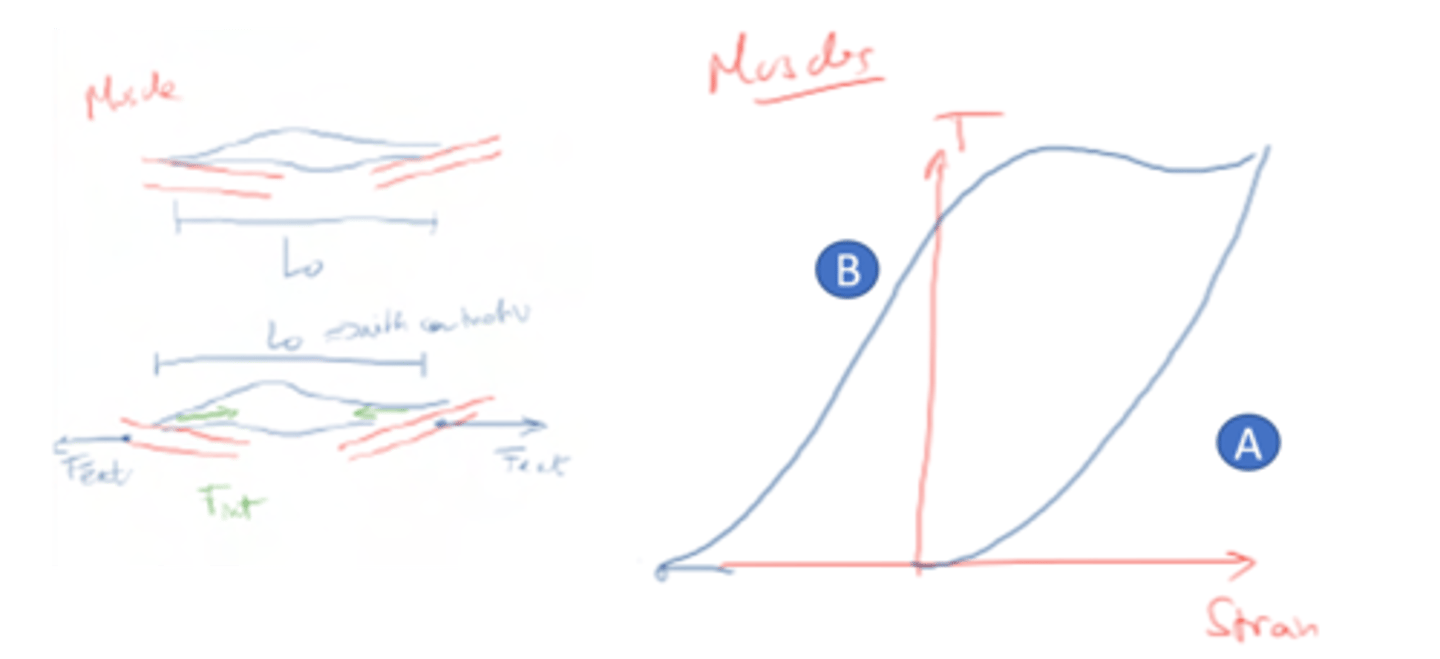
Characteristic of tensile stress on muscles

. In zone A, the muscle is not contracted. It behaves as a tendon/ligament

. In zone B, the muscle is contracted. The curve is shifted to the left.

With T=0 (no stress) the muscle length is lower than at rest (stress is negative).

Elastoplastic materials

Both plastic and elastic regions coexist for the same stress.

Considered liquid materials (ie plasticine).

Poisson Ratio

It is the negative ratio of transversal strain or lateral strain to the longitudinal strain of a material under stress.

Poisson's ratio values are between -1.0 and 0.5 (theoretical) even most of materials are between 0 and 0.5

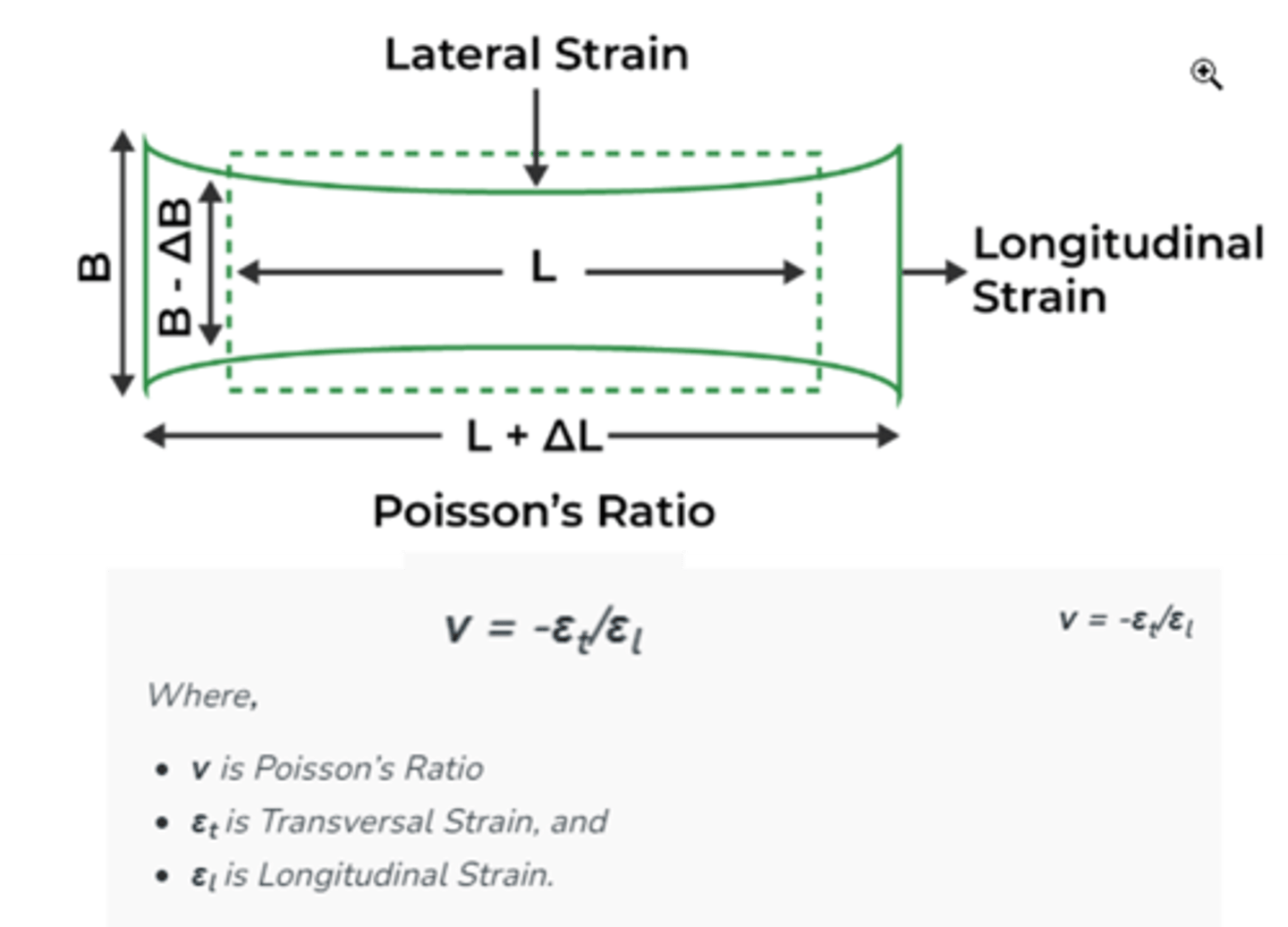
Poisson Ratio of zero means

There is no lateral reduction in diameter when the material is elongated but density decreases

Young Modulus and Poisson ratio are enough to describe the behaviour of a material?

Yes, if it simple (homogeneous and isotropic)

A fracture happens when

the stress force breaks the chemical bond and this propagates as a mechanical wave. The velocity of propagation is almost instantaneous.

Modes of fracture

2 for shear stress

1 for tensile stress

Compressive stress produces fracture due to the tensile stress provokes while pressing. So, iti is the tensile stress who is provoking the fracture

Fatigue

Material under repetitive stress every time resists less stress becoming weaker at every cycle.

In ligaments, in example, is due to some fibers that starts to be broken

To induce fatigue is necessary to cross the ____________________

Yield point (point defining the end of the elastic area)

The tension that a muscle can produce depend on the initial length of the __________________

Sarcomere

Sarcomere tension depend on the interaction between the ______________ and the _____________

actin myosin

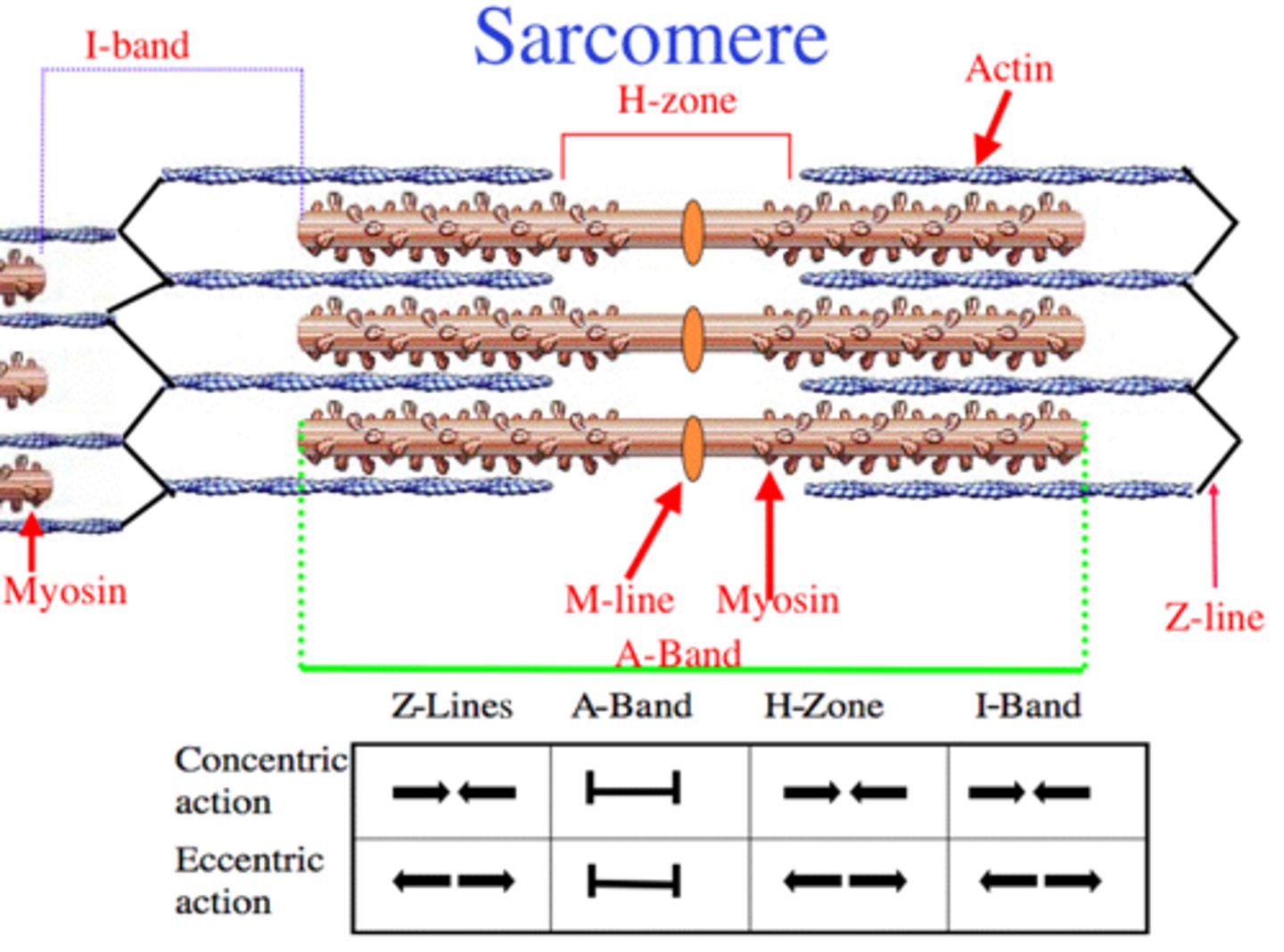
The longer the muscle the _____________ the total force/tension

greater

Muscle passive tension

It is due to the elastic behaviour of the muscle

Muscle active tension

The muscle is stimulated to control

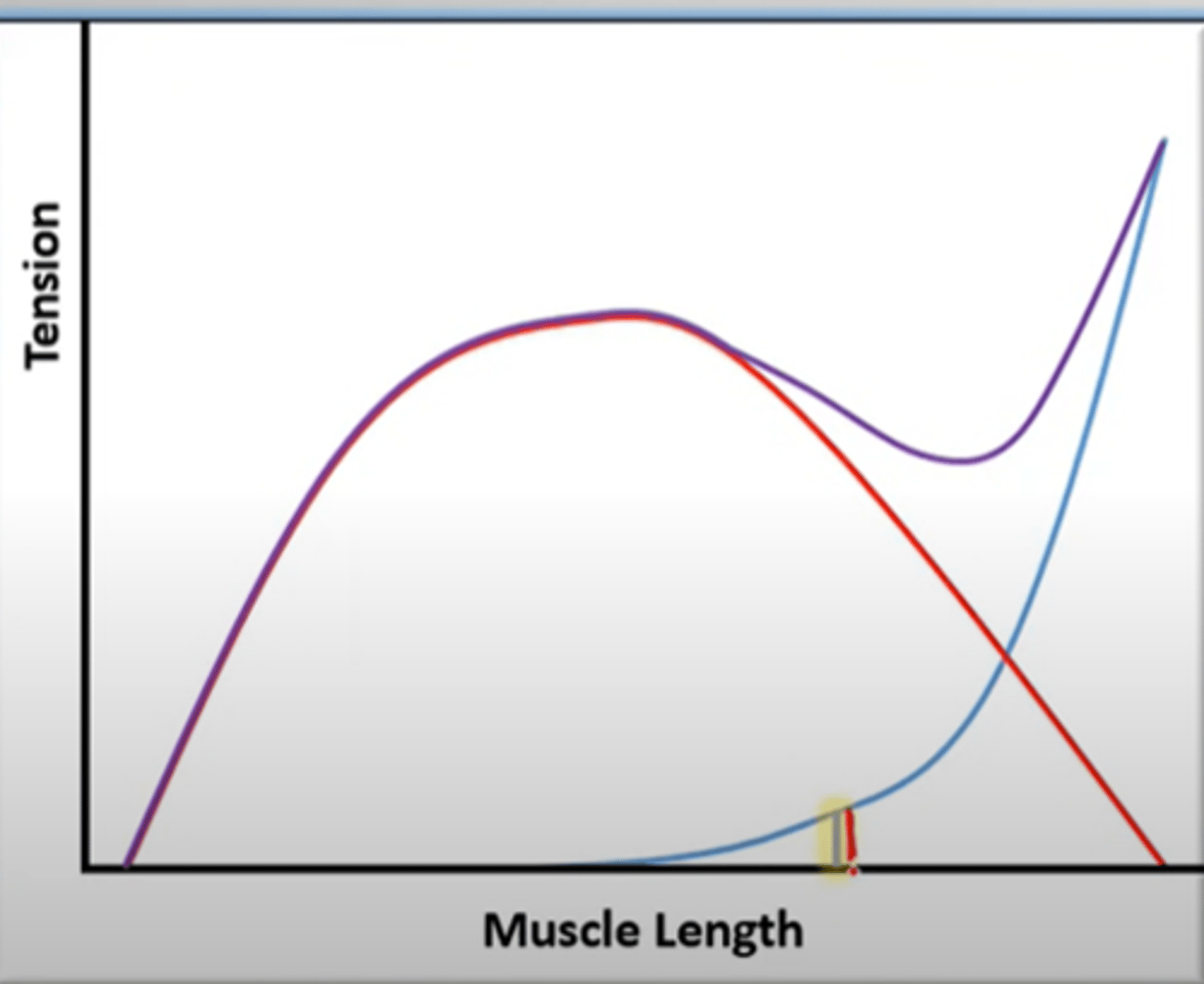
Muscle tension vs length

Total tension (purple) = active (red)+ passive (blue)

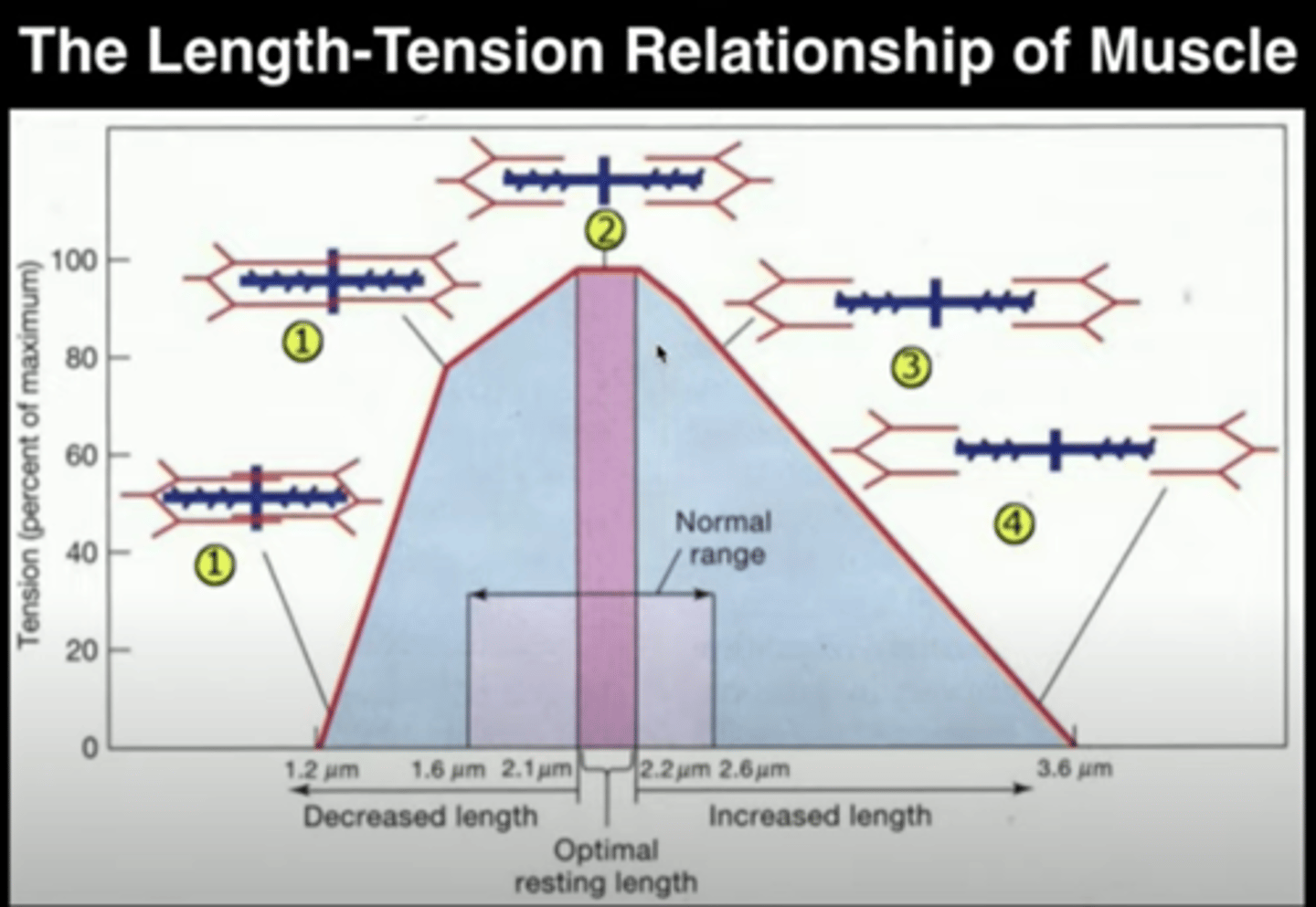
Sarcomers vs muscle length

Fatigue happens when the strain points exceeds the ____________________

yield point

After exceeding the yield point and being under fatigue the stress needed to achieve same length is ___________________

lower

Bending a beam, the bending moment is proportional to __________________ and ____________________ and inversely proportional to the _________________

Young module, moment of inertia, radius

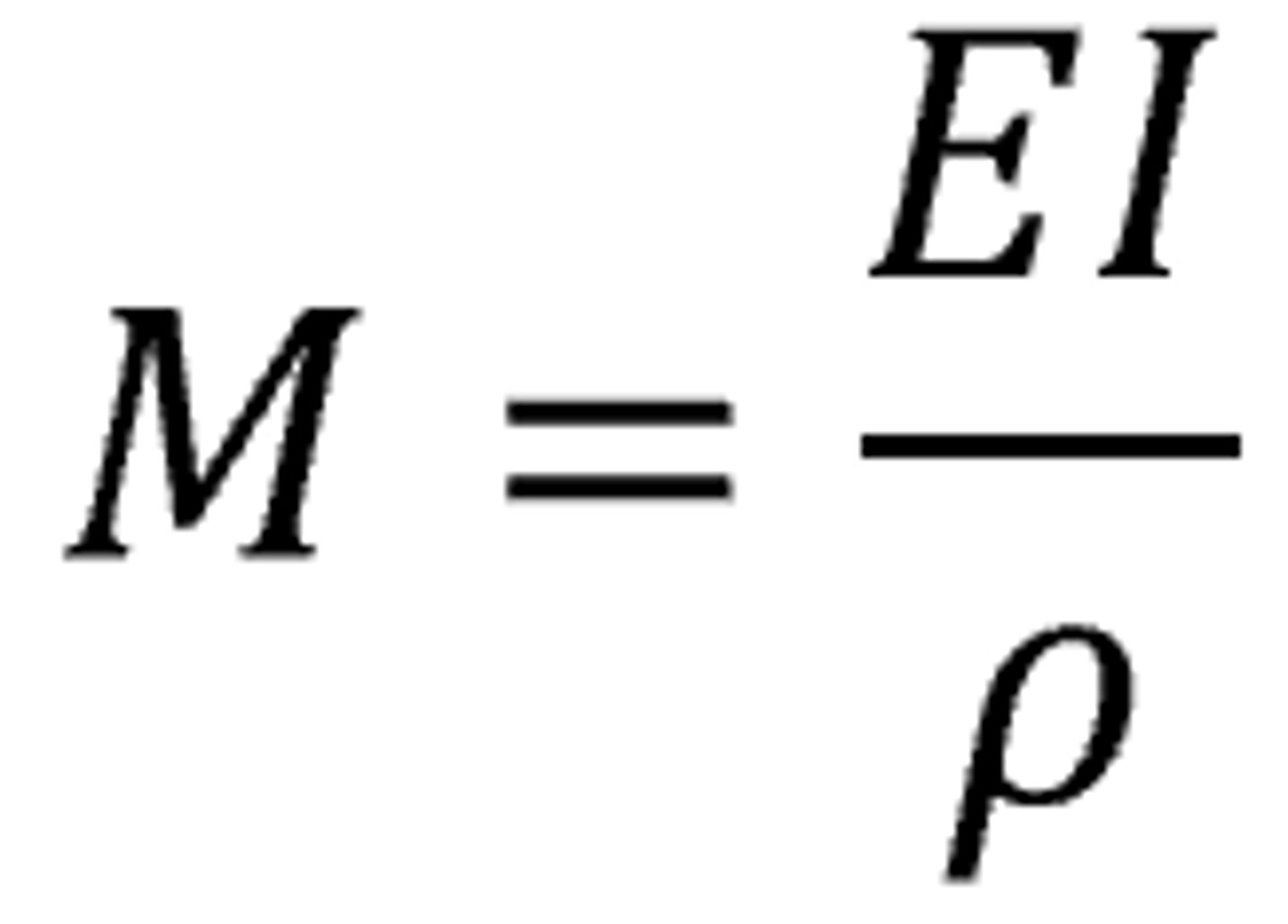
Torsion of a beam produces a torsion moment proportional to the shear module and shear momentum inertia and deformation

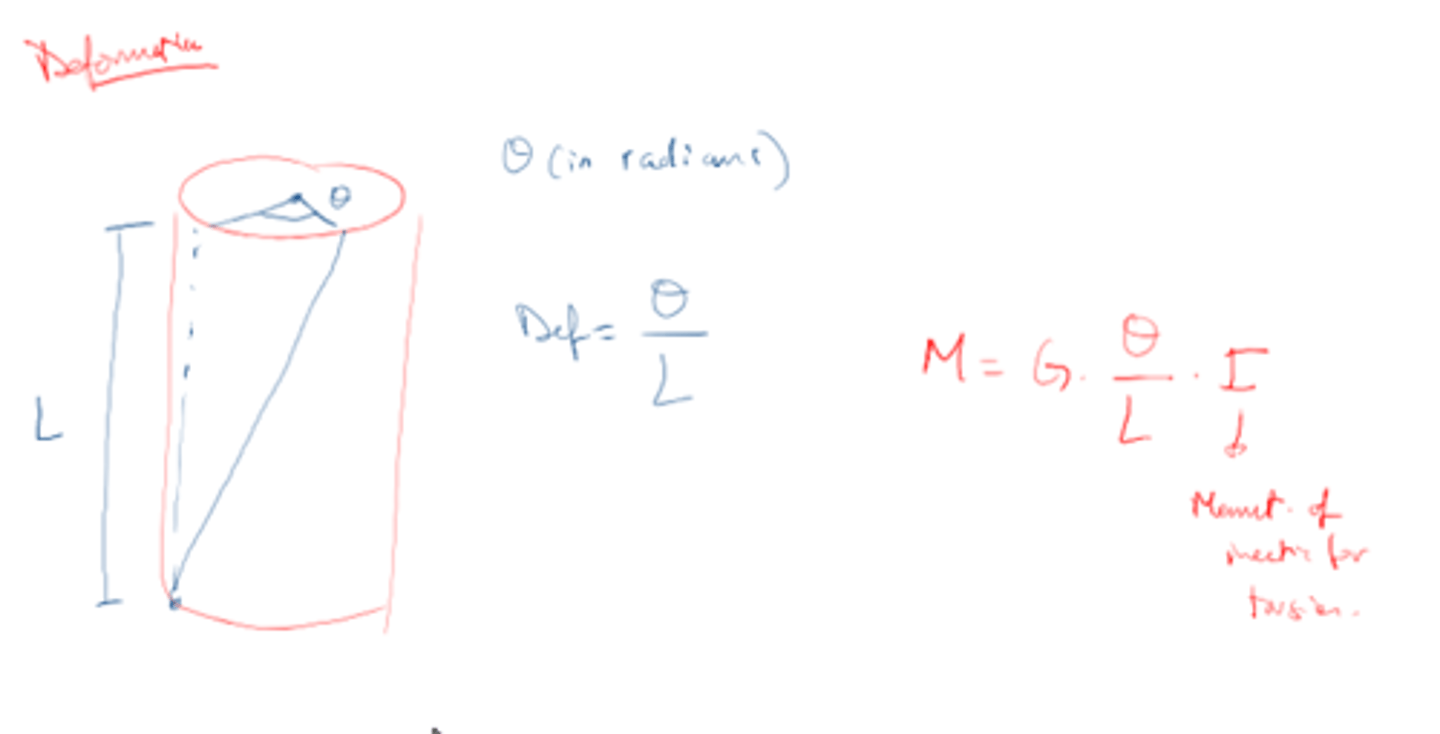
The higher the moment of inertia of a beam the _____________ the bending for an applied force

lower

Moment of inertia depends on the _______________ of the beam

cross section or shape

Laplace's law

The stress in a cavity is proportional to the pressure and the radius and inversely proportional to the thickness

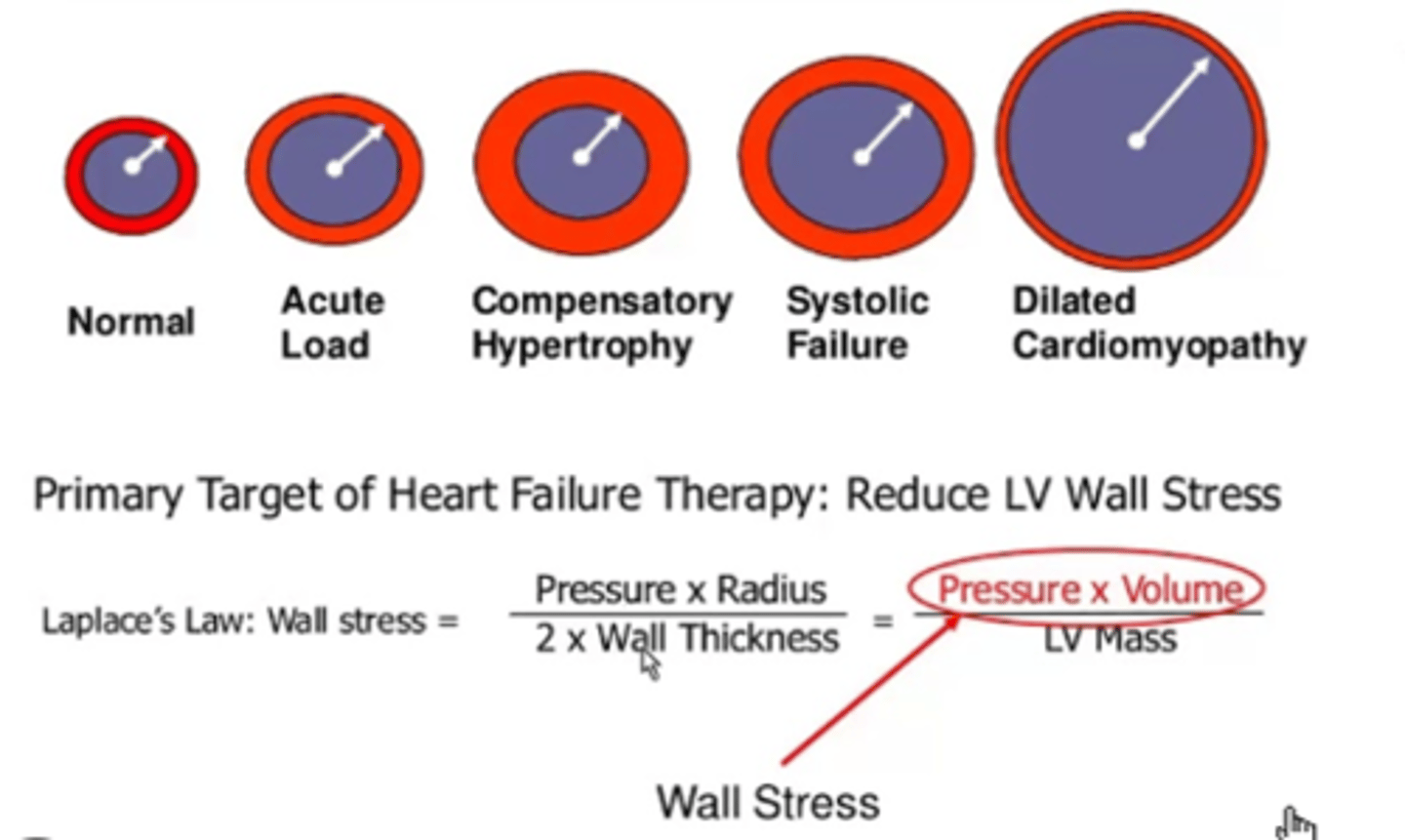
Elasticity question

Elasticity question (II)

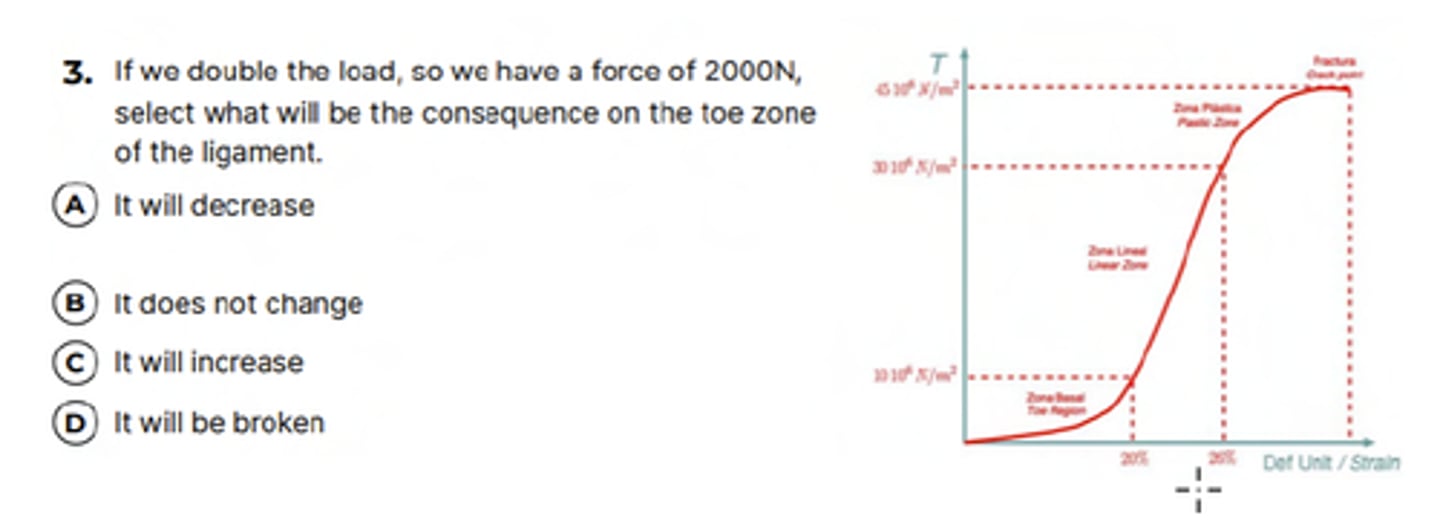
Elasticity question (III)

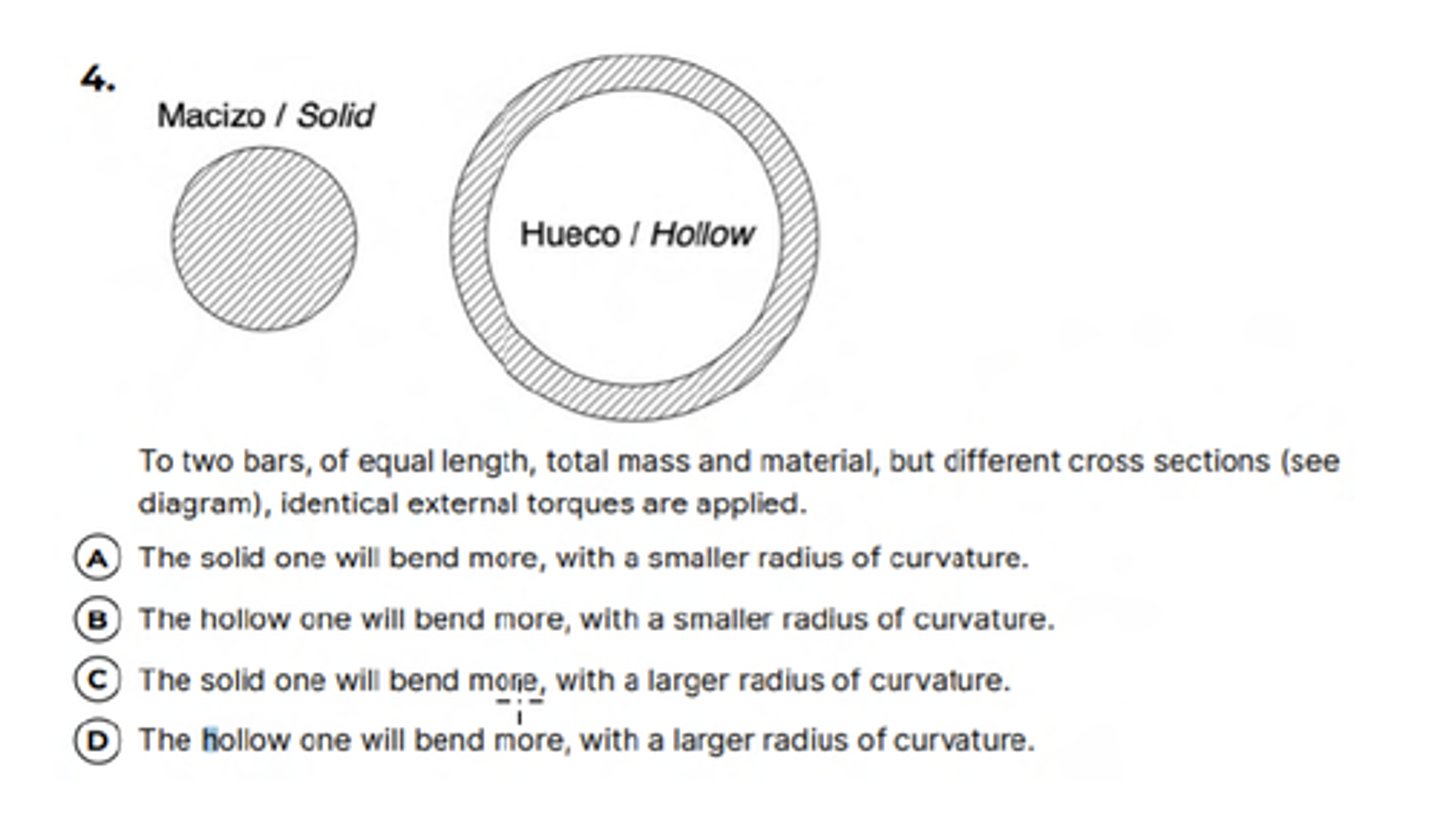
Elasticity question (IV)