AP Precalc Flash Cards

A model is considered appropriate for a data set if the residual plot…

Appears without pattern

The distance between a point on a polar function r=f(θ) and the origin is decreasing if…

r is positive and decreasing or r is negative and increasing

(|r| is decreasing)

The slope of a function at any given point gives…

The rate of change of the function at that input.

f(cx)

horizontal dilation by a factor of 1/c

secθ =

cscθ =

cotθ =

1/ cosθ

1/ sinθ

1/tanθ = cosθ / sinθ

a polynomial of degree n has…

• exactly n complex zeros

  • (real or imaginary)

• constant nth differences

• at most n-1 extrema

domain and range of y=arctan x

domain = (-∞, ∞)

range = (-π/2, π/2)

key features of y=b^x

where b>1

Domain = all real numbers

range = y>0

horizontal asymptote at y = 0

increasing and concave up over entire domain

to determine the end behavior of a rational function…

analyze the ratio of leading terms

given (x,y) in cartesian coordinates, determine polar coordinates, (r, θ)

r = (√x² + y²)

θ = tan^-1 (y/x)

*add π if angle is in Q2 or Q3

a positive residual indicates that the predicted values is an…

underestimate

end behavior of a polynomial f with an even degree and a negative leading coefficient

lim f(x) x →∞ = -∞

lim f(x) x →-∞ = -∞

key features of y=sinx

domain = all real numbers

range = [-1,1]

period = 2π

amplitude = 1

midline = y=0

passes through = (0,0)

log_b(b) =

1

a relative minimum occurs when a function f…

changes from increasing to decreasing

the average rates of change of a linear function are…

constant

if a rational function, f, has a vertical asymptote at x=a, then

lim f(x) x →a^- =

lim f(x) x →a⁺ =

lim f(x) x →a^- = ± ∞

lim f(x) x →a⁺ = ± ∞

a function f is concave up if…

the rates of change f are increasing

explicit rule for nth term of an arithmetic sequence given common difference d, and the a_k term

a_n = a_k + d (n-k)

a polar function r = f(θ) is decreasing if…

as θ increases, r decreases

end behavior of a polynomial f with an even degree and a positive leading coefficient

lim x→∞= ∞

lim x→-∞ = ∞

absolute maximum

the greatest output of a function

log_bm^k

klog_bm

f(x-c)

horizontal translation c units to the right if c>0

or

c units to the left if c<0

domain and range of y= arcsin x

domain = [-1,1]

range = [-π/2,π/2]

a function f(x) = ab^x demonstrates exponential decay if…

0 < b < 1

a function f is decreasing on an interval if…

as the input values increase the output values always decrease

or

for all a and b in the interval if a < b, then f(a) > F(b)

y = tan(bx) has a period of…

π/b

odd function

f(-x) = -f(x)

a function is exponential if as input values change ___, output values change ____.

additively

multiplicatively

average rate of change of f on the interval [a,b]

f(b) - f(a) / b - a

pythagorean identities

sin² θ + cos² θ = 1

1 + cot² θ = csc² θ

tan² θ + 1 = sec² θ

residual

actual value - predicted value

a function is logarithmic if as input values change ____, output values change _____.

multiplicatively

additively

point of inflection

point on the graph of a function where the concavity changes, indicating a maximum or minimum rate of change

cos(2θ)

cos² θ - sin² θ

is equivalent to

2 cos² θ - 2

and

1 - 2 sin² θ

in the y-axis is logarithmically scaled then…

equal sized increments on the y-axis represent proportional changes in the output variable

key features of y = log_b x where b>1

domain = x>0

range = all real numbers

vertical asymptote = x = 0

increasing and concave down over entire domain

cf (x)

vertical dilation by a factor of c

sin(2θ)

2 sin θ cos θ

in a semi-long plot where the y-axis is logarithmically scaled, exponential functions will appear…

linear

e^{a ln b} =

b^a

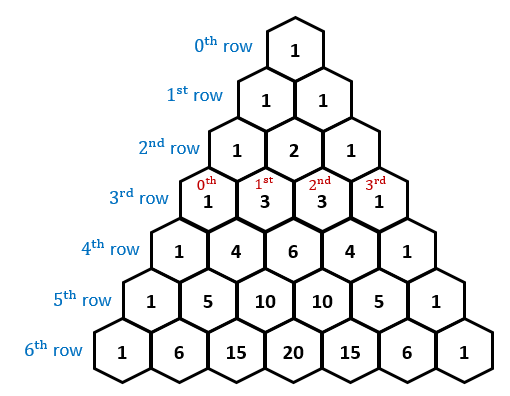
pascal’s triangle

an arrangement of binomial coefficients in triangular form

if a rational function, f, has a horizontal asymptote at y = b, then…

the ratio of leading terms is a constant b

lim f(x)→∞ = b, and lim f(x)→-∞ = b

domain and range of y= arccos x

domain = [-1,1]

range = [0,π]

the distance between a point on a polar function r = f(θ) and the origin is increasing if…

r is positive and increasing

or

r is negative and decreasing

*(|r| is increasing)

multiplicity

the number of times a factor occurs in a polynomial function

determine the amplitude, period, midline, and phase shift of

f(x) = a sin(b(x-c))+d

amplitude = |a|

period = 2π / b

midline = y = d

phase shift = c units to the right

a rational function has a vertical asymptote at x = a if…

x = a is a zero of the denominator but NOT the numerator

what does the constant e represent?

the base of growth for all continually growing processes

e = 2.718

log_b(1) =

0

givewn (r,θ) in polar coordinates, determine cartesian coordinates, (x,y)

x = r cos θ

y = r sin θ

log_b(mn)

log_b m + log_b n

if a rational function, f, has a hole at (a, L) then

lim f(x)→a^- = lim f(x)→a⁺ = ____.

lim f(x)→a^- = lim f(x)→a⁺ = L

end behavior of a polynomial f with an odd degree and a positive leading coefficient

lim f(x)→∞ = ∞

lim f(x)→-∞ = -∞

a relative maximum occurs when a function f…

changes from increasing to decreasing

a function f in concave down if…

the rates of change of f are decreasing

key features of y = cos x

domain = all real numbers

range = [-1,1]

period = 2π

amplitude = 1

midline = y=0

passes through = (0,1)

for rational functions, a slant asymptote occurs when

the degree of the numerator is exactly one more than the degree of the denominator

one-to-one function

function where each input has a unique output (no repeated outputs)

the average rates of change of a quadratic function…

are changing at a constant rate

or

follow a linear pattern

even function

f(-x) = f(x)

a negative residual indicates that the predicted value is an…

overestimate

f and g are inverse functions if…

f(g(x)) = g(f(x)) = x

f(-x)

reflection over the y-axis

f(x) = cot x has a vertical asymptote at..

x = πk, where k is an interger

a function is quadratic if over equal-length input intervals, output values…

change by constant second difference

sin(α±θ)

sin α cos θ ± sin θ cos α

b^x-c =

b^x / b^c

a rational function has a hole at x = a if

x = a is a zero of the numerator AND the denominator

if x = a is a real zero of a polynomial with an even multiplicity, then…

the graph of the polynomial is tangent to the axis at x = a

a negative rate of change indicates that the function output is…

decreasing

f(x) = tan x has a vertical asymptote at…

x = π / 2 + πk. where k is an integer

-f(x)

reflection over the x-axis

error (in a model)

predicted value - actual value

a function is linear if over equal-length input intervals, output values…

change by a constant amount

cos (α ± θ)

cos α cos θ ∓ sin α sin θ

b^x+c =

b^x x b^c

a positive rate of change indicates that the function output is…

increasing

if x = a is a real zero of a polynomial with an odd multiplicity, then

the graph of the polynomial passes through the x-axis at x = a

a rational function has a zero at x = a if…

x = a is a zero of the numerator but NOT the denominator

tan θ gives the ____ of the terminal ray of θ.

slope

a function f(x) = ab^x demonstrates exponential growth if…

b > 1

a function f is increasing on a interval if…

as the input values increases the output values always increase

or

for all a and b in the interval if a < b then f(a) < f(b)

absolute minimum

the least output of a function

log_b (m / n)

log_b m - log_b n

f(x) +c

vertical translation c units up if c > 0

or

c units down if c < 0

explicit rule for nth term of a geometric sequence given common ratio r, and the a_k term

a_n = a_k x r^n-k

a polar function r = f(θ) is increasing if…

as θ increases, r increases

end behavior of a polynomial f with an odd degree and a negative leading coefficient

lim f(x)→∞ = -∞

lim f(x)→-∞ = ∞