ribos ir išvestinės

suspaudimo teorema

kai f(x)≤g(x)≤h(x). o x yra arti a, tuomet ribos artėjančios į a lim f(x) = lim h(x) =L tuomet ir g(x) = L

trigonometrinių funkcijų ribos

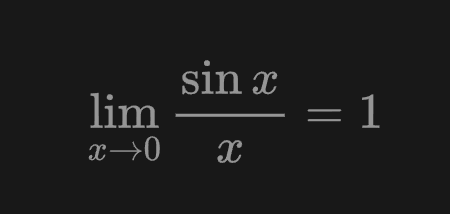
banginio riba

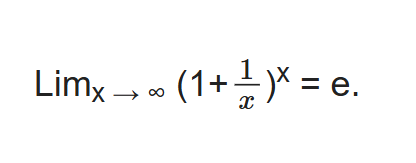
skaičiai pakelti begalybe

jei 0.0…. tai =0, o jei normalus tai ∞

vienpusės ribos

-=iš kairės, +=iš dešnės, papras tas be ženklis limitas egzistuoja tik tada, kai ir + ir - limitai lygūs tai pačiai reikšmei

tolydi funkcija

1) turi priklausyt apibrėžimo sričiai (pilnas taškas)

2) turi egzistuot lim a (ne tik - arba +)

3) f(x)=f(a) žodžiu utas taškas neskraido kažkur o yra būtent tas prie kurio artėja

funkcija tolydi iš dešnės/kairės

gali būt ne pilnai tolydi o tsg iš vienos pusės: funkcija f yra tolydi iš kairės taške a , kai funkcijos x artėjantis link a lygus f(a)

intervale tolydi funkcija

aki funkcija tolydi viduode intervalo taškuose

jeigu funkcijos f ir g yra tolydžios o c yra konstanta tada šitos funkcijos irgi tolydžios

1) f+g 2) cf 3) f/g 4) f-g 5) fg

kada funkcija vadinama diferencijuojama

1) taške a kai kai egzistuoja f’(a)

2) difeencijuojama interva (a,b) kai yra diferencijuojama visuose šio intervalo taškuose

kada funkcija NEdiferencijuojama

1) yra smaigalys

2) yar netolydumas

3) jei liestinė yra statmena ox ašiai

funkcijos stacionarieji taškai

taškai kuriuose išvestinė lygi 0

funkcjios ekstremumai

taškai kuriuose funkcija lygi 0 ARBA NEEGZISTUOJA

minimumas

jei taško x aplinkoje funkcija yra didesnė

maximumas

jei taško x aplinkoje funkcija yra mažesnė

žemyn iškila funkcija

kai nubrėžta liestinė yra žemiau funkcijos 🙂 +

aukštyn iškila funkcija

kai nubrėžta liestinė yra aukščiau už funkciją ☹ -

vingio/perlinkio taškas

taškas pro kurį einanti funkcija keičia savo iškilimo pobūdį

kokios būna funkcijos asimptotės

vertikalios horizontalios pasvirosios

kokie būna neapibrėžtumai

1. 0/0 2. ∞/∞ 3. ∞-∞ 4. 0x∞ 5. 0*0 6. 1*∞

Išvestinė

tai dydis, rodantis kaip greitai kinta funkcija, kai kinta jos argumentas.