USU GEOG 2800 Midterm

Definition of GIS

Definition of Spacial Thinking

Find meaning in the shape, size, orientation, location, direction or trajectory, of objects, processes, or phenomena.

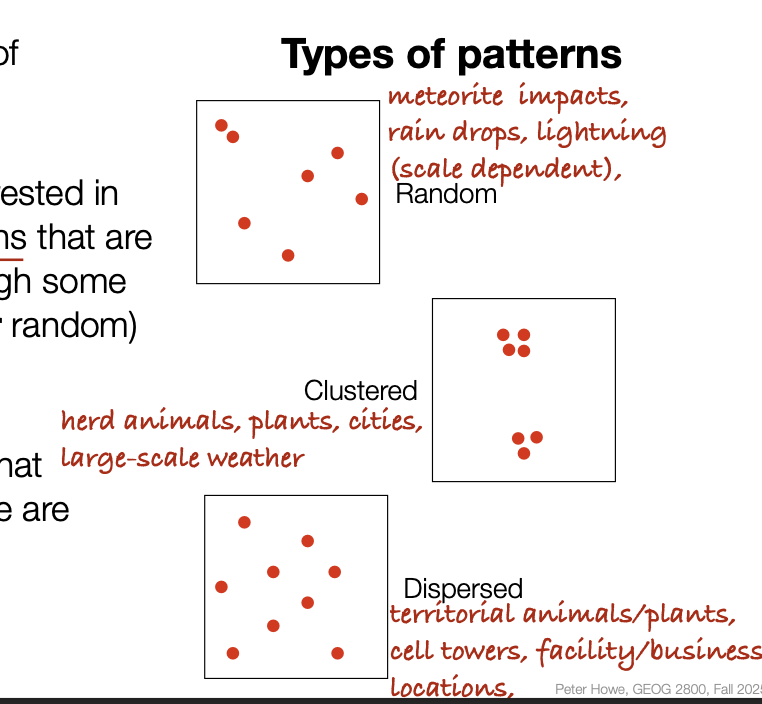
Types of Spacial Patterns

Radom, Clustered, Dispersed

Why is spacial data important?

In order to solve problems and better understand the world, we need to ask questions, develop hypotheses, and question assumptions.

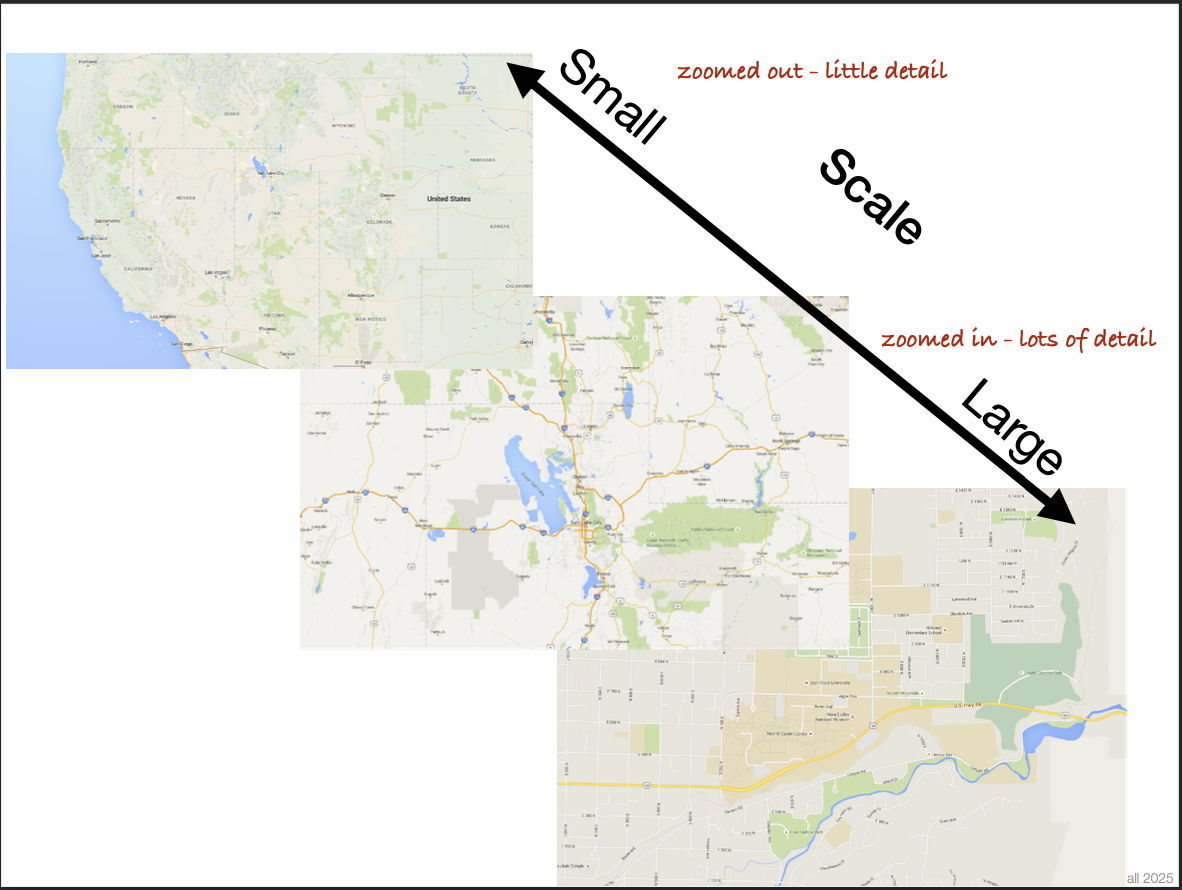
Small vs Large Scale

Small scale is zoomed out with little detail. Large Scale is zoomed in with a lot of detail

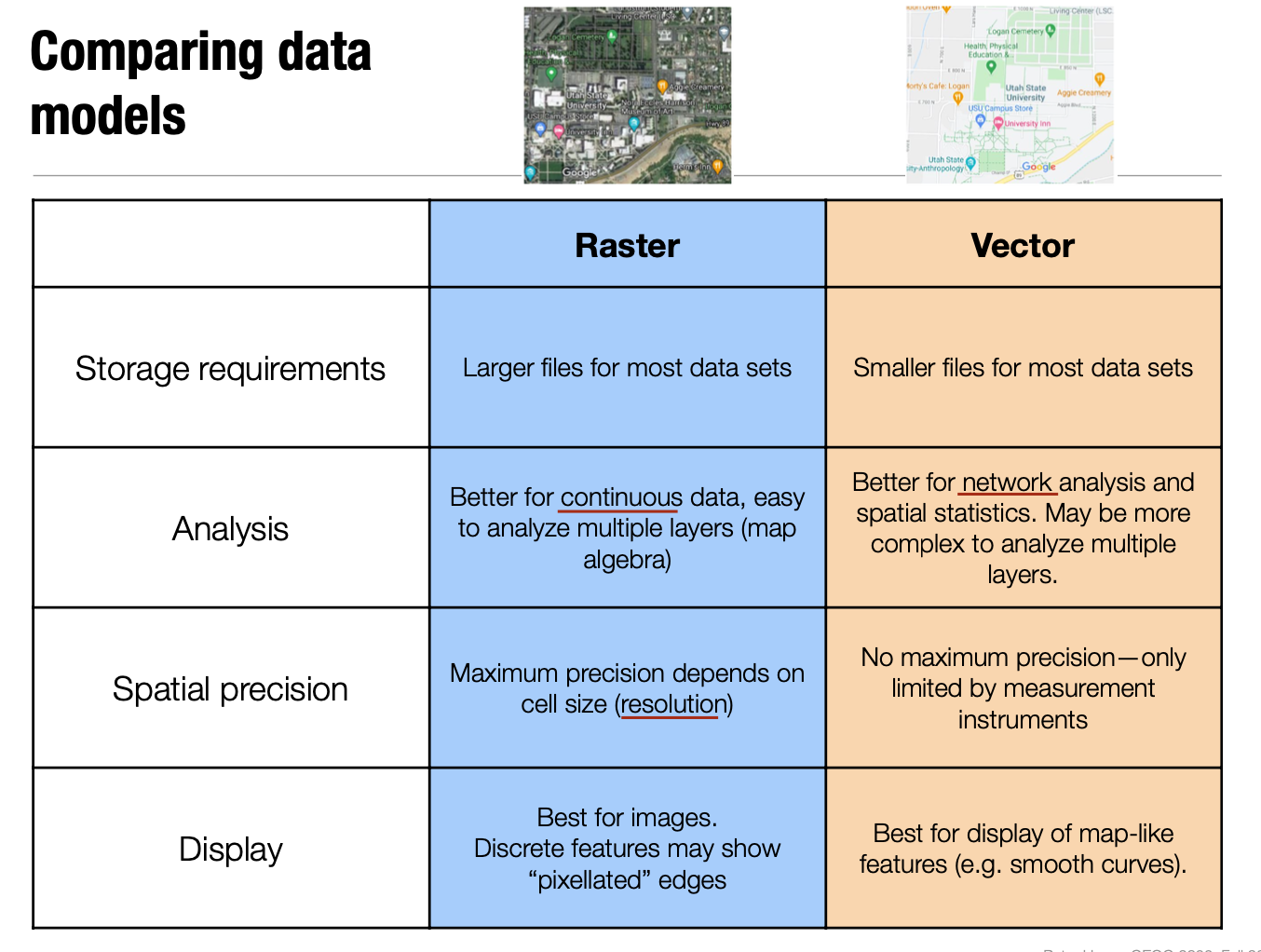
Vector data:

Lines, points, and polygons. Has attribute, locational, and topological data.

Topological Data

Shows spacial relationships and describes how spatial data share geometric attributes

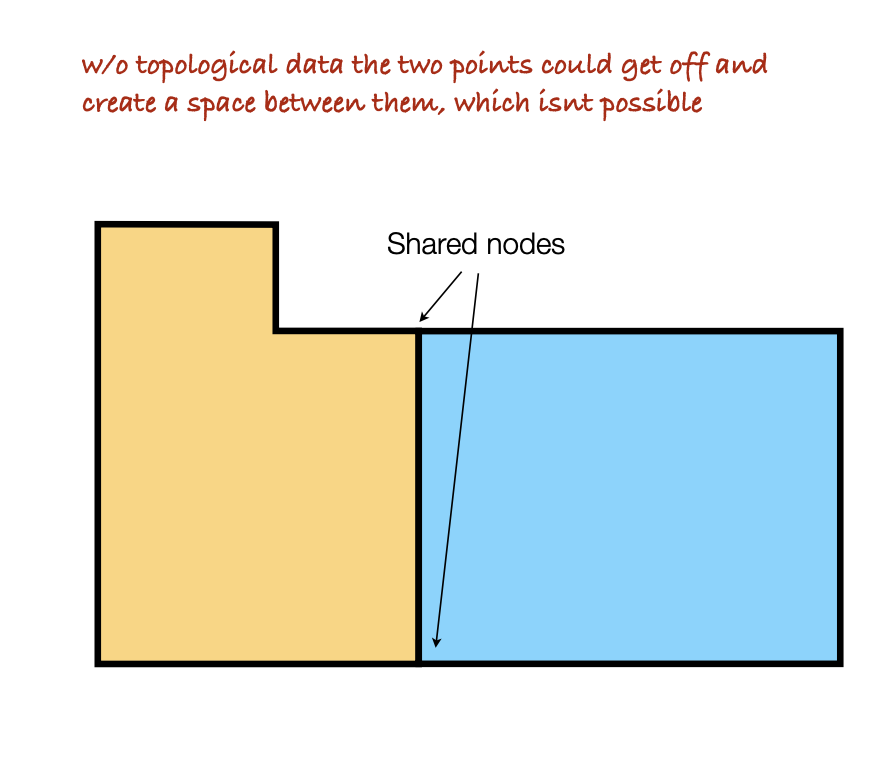
Types of Topology information:

Adjacency: info about neighborhoods of different objects.

Enclosure: info about spatial features that enclose other features.

Connectivity: info about the links between spatial objects.

Vector Advantages:

Precise location of features, store attributes, flexible and easy to edit, smaller files, suitable for anaysis or areas, lenths, and networks.

Vector Disadvantages:

Features seem homogenous, difficult to show gradients, imply discrete division that might not exist, and accuracy depends on scale.

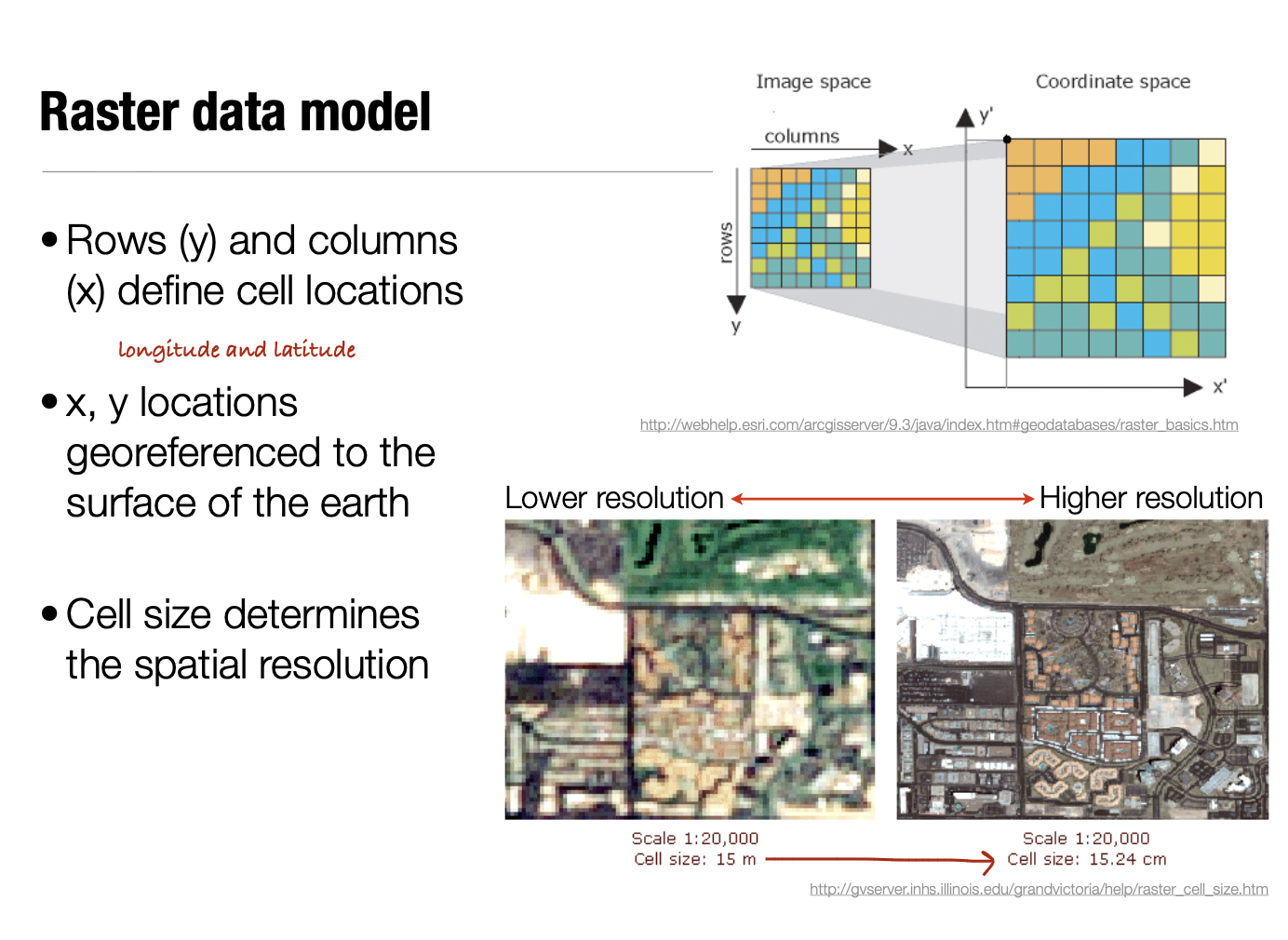
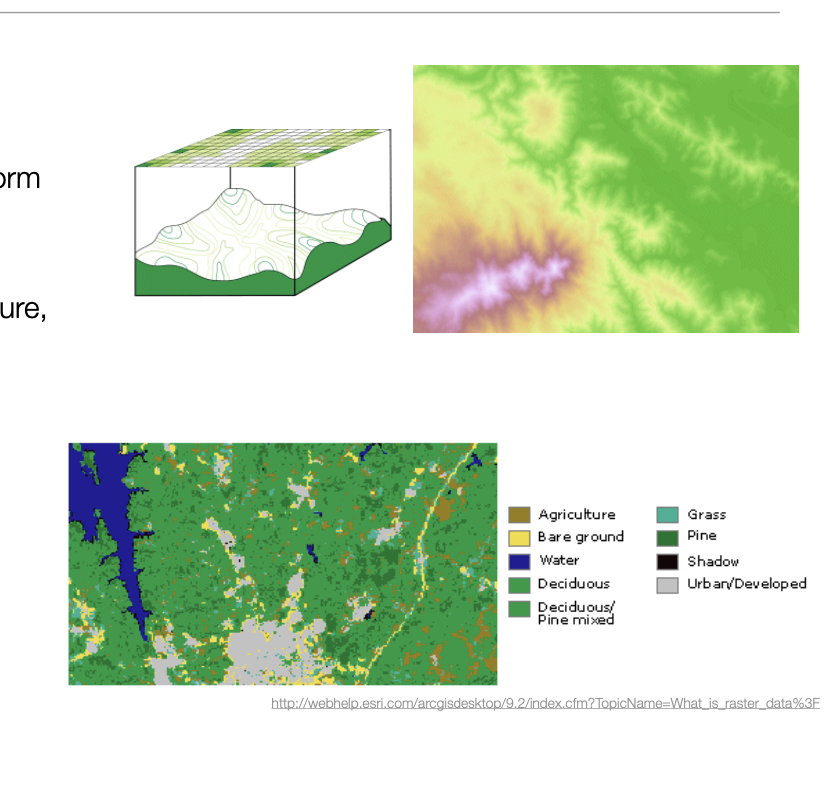
Raster Data:

Divides space into grid cells or pixels, each cell is spacial locations, size is constant, each cell has a value/attribute.

Raster Data Types:

Continuous rasters: Shows gradual changes / cell values vary continuously to for surface. Ex: elevation, temp., density.

Discrete rasters: classifies data into categories. Ex: land cover, soil types, species comp.

Raster vs Vector Data Models

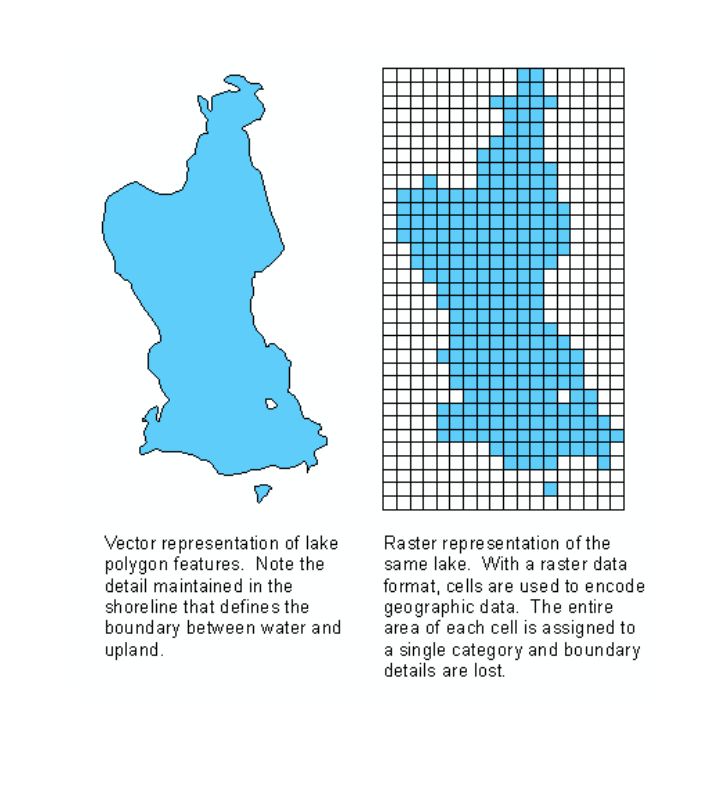
Rasterization:

Creating a raster from vector data. You superimpose a grid over vector data, its sensitive to raster resolution (cell size), and information is lost.

Vectorization:

Creating vector data from raster data. Combine areas with similar values into polygons or locate similar areas with lines. Its sensitive to raster resolution and information is lost.

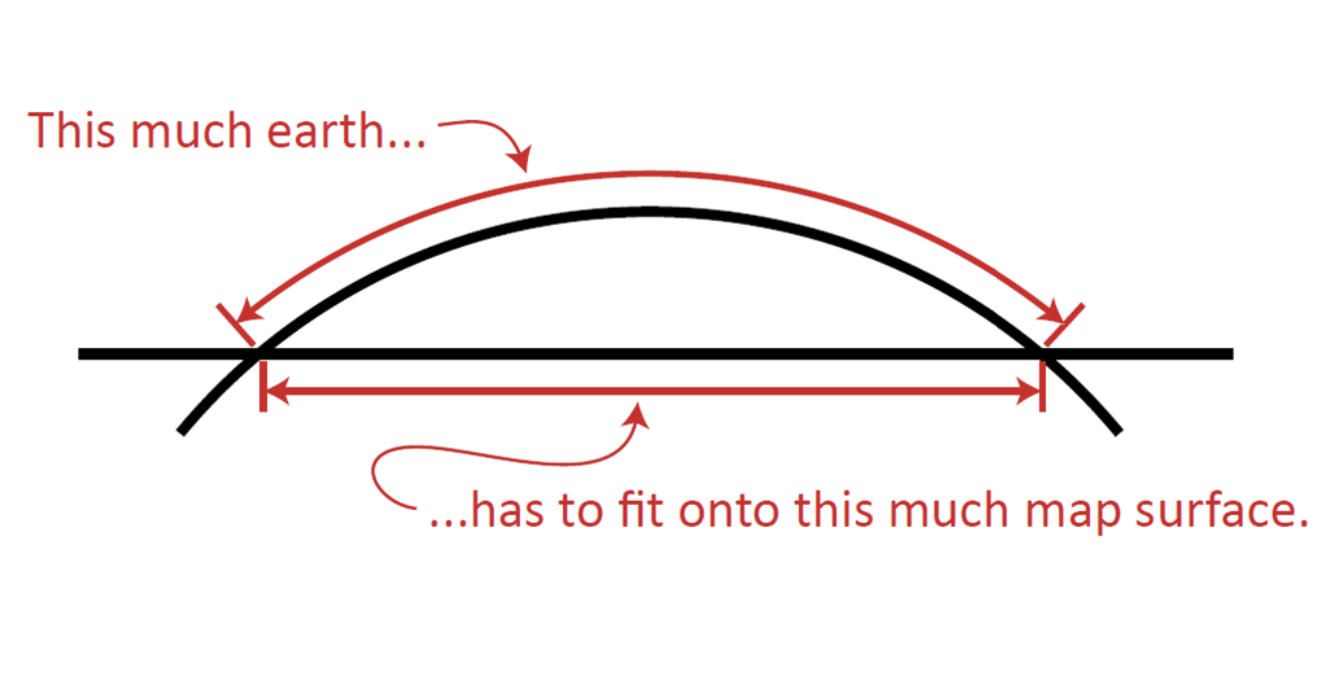
Map Projections:

How to transform coordinates on the earth into a flat 2-D surface.

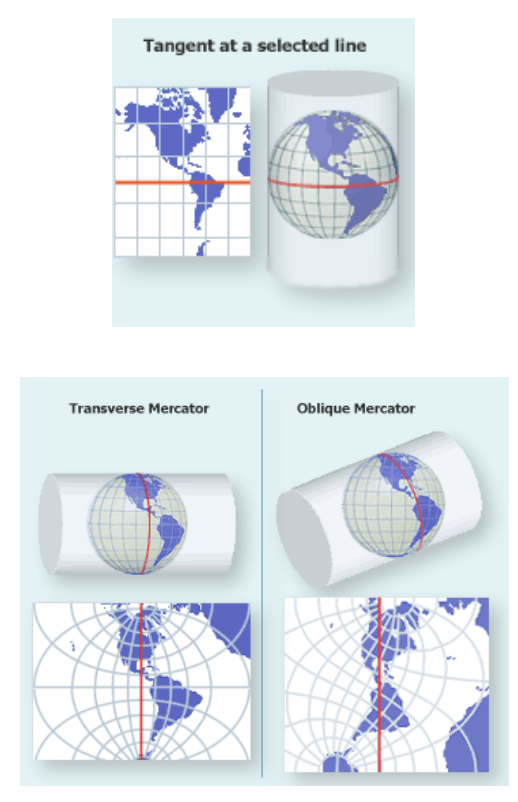
Aspect in Map Projections, Normal, Transverse, and Oblique Aspect.

Aspect: the orientation of the developable surface.

Normal Aspect: the standard line is the equator.

Transverse Aspect: the standard line is a meridian.

Oblique Aspect: the standard line is a great circle other than the equator or prime meridian.

Types of Distortion/Accuracy:

Equal-area: accurately represents areas/relative sizes.

Conformal: accurately represents shapes / intersecting lines, and maintains the angles

Equidistant: accurately represents distances along certain straight lines on the map

No map can be both equal-area and conformal

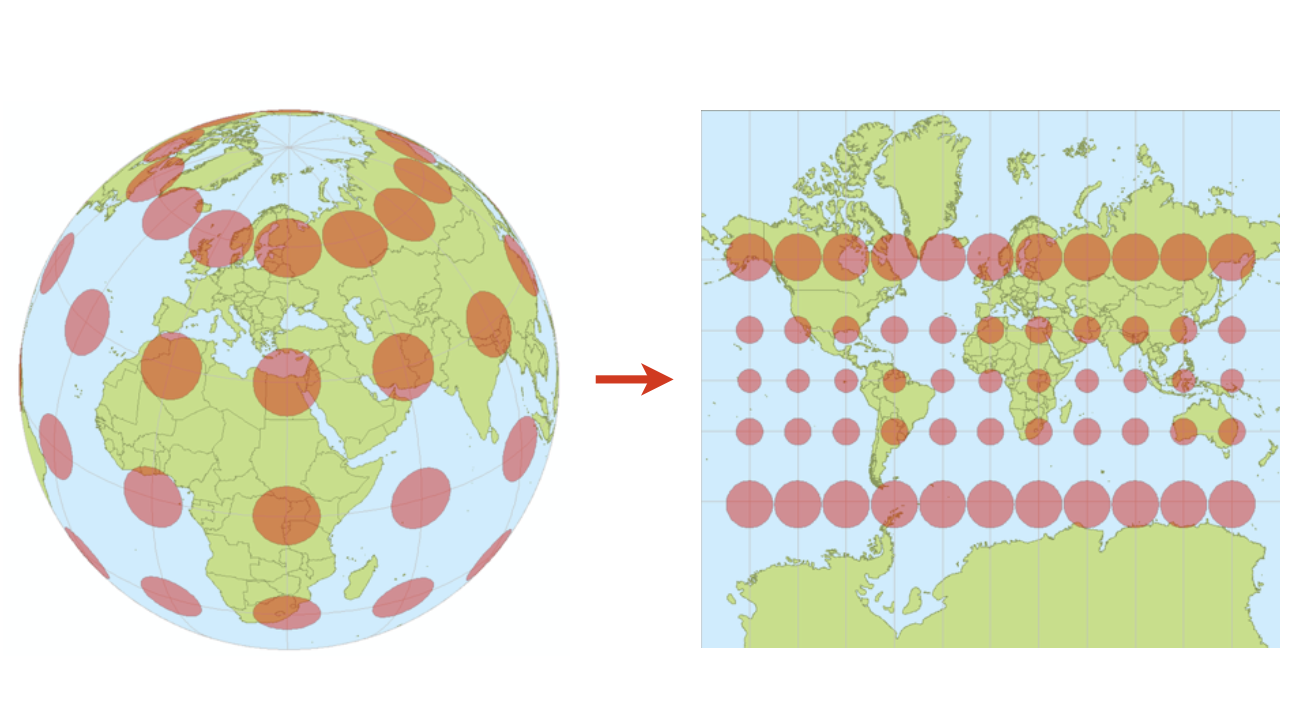
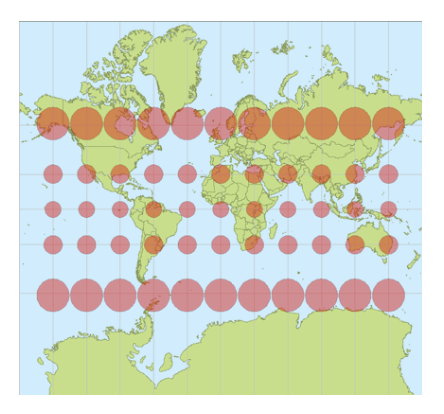
Indicatrix

Small circles on the globe placed at the intersection of grid lines to visualize distortion.

Conformal Projections  

Shapes and angles are accurate, but size is distorted. Can be a Mercator or Conic Conformal projections.  

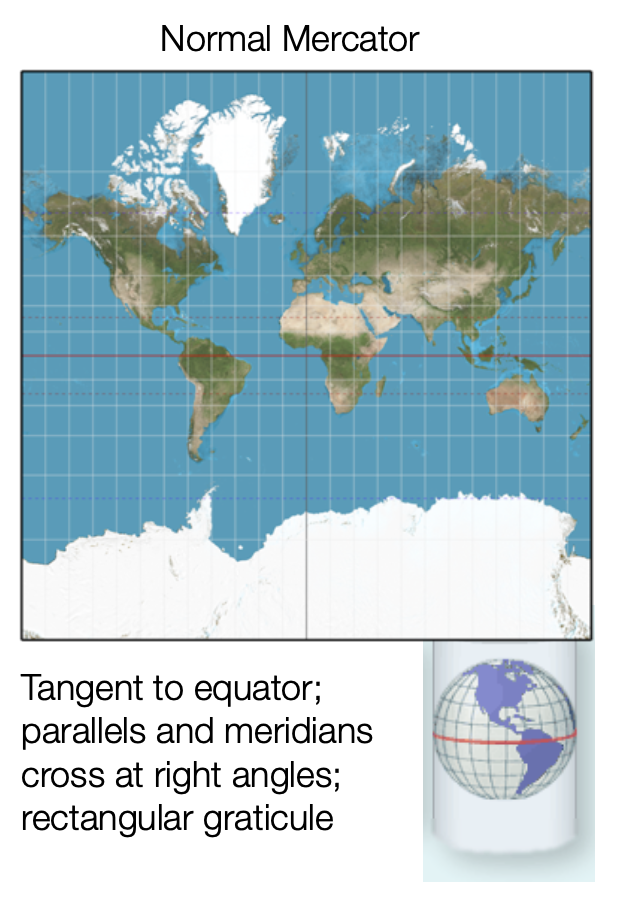
Cylindrical Mercator 

Conformal Map, tangent to Equator 

Lambert Conformal Conic

Accurately represents shapes around mid-latitudes. Often used for regional or continental maps.

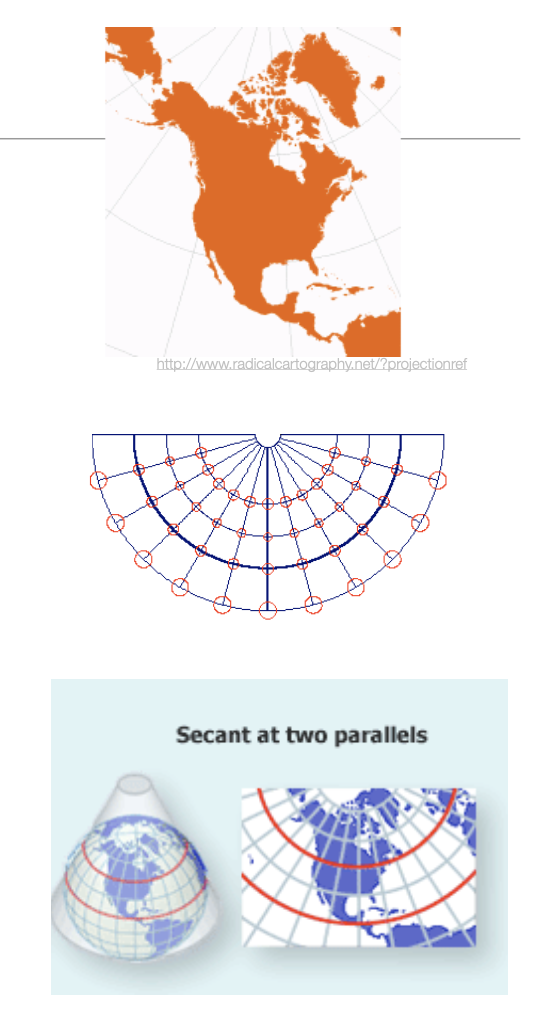
Equal Area (Equivalent)

Sizes and ratios throughout the map are consistent, which is useful for comparing the size and extent of geographic areas. Can be Albers Equal Area Conic, Gall-Peters, or Mollweide.

Great Circle

The intersection of the surface of a sphere with a plane that passes through the center of the sphere.

• Divides the sphere into two equal halves

• The shortest distance between any two points on the surface of the Earth is always along a great circle

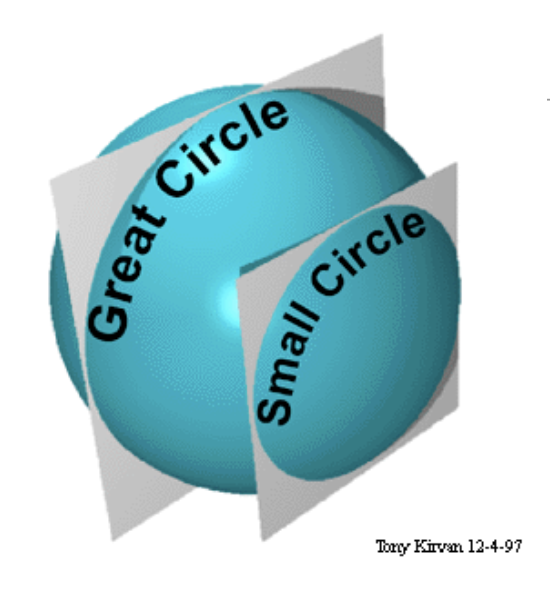
Small Circle

Small circle: the intersection of the surface of a sphere with a plane that does not pass through the center of the sphere

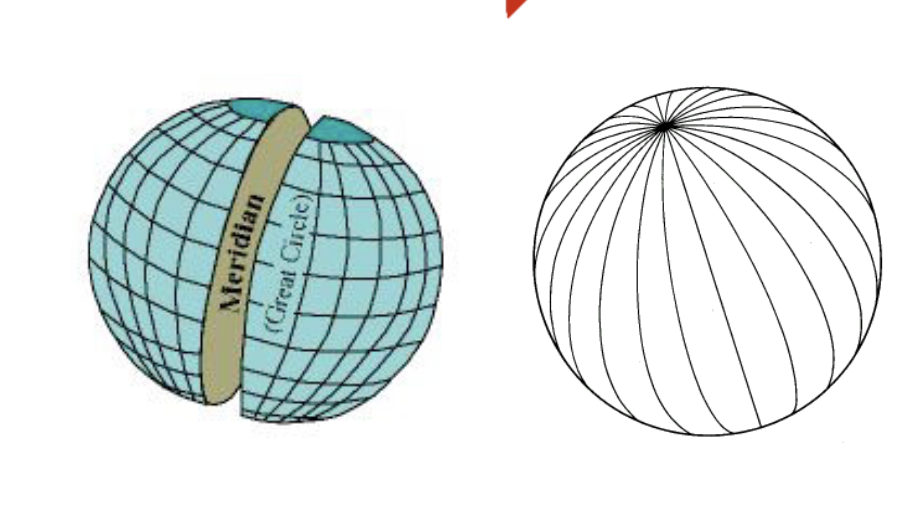
Meridians

Meridians, lines of equal longitude, are also great circles with a plane parallel to the axis of rotation of the earth. All meridians intersect at the poles, there are an infinite number of meridians

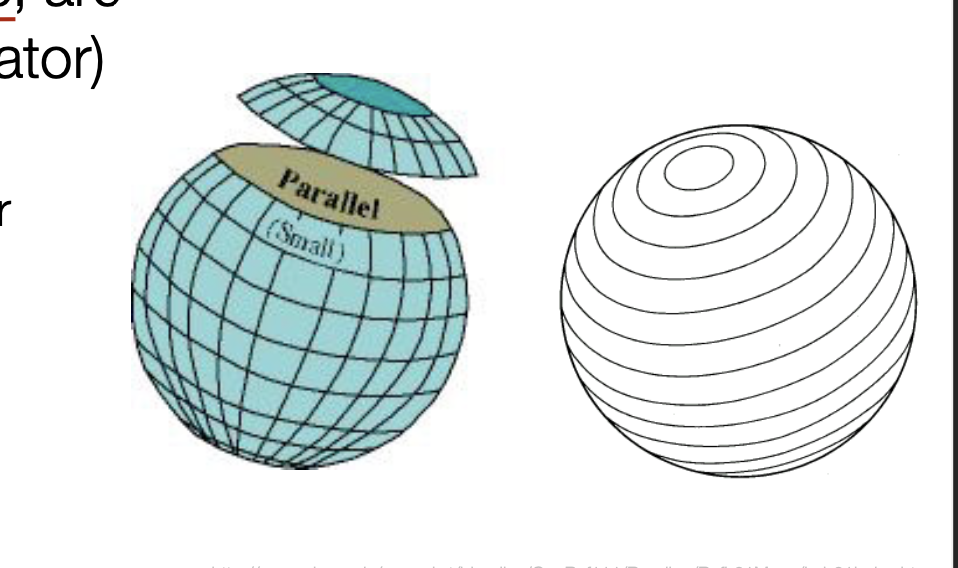
Parallels

Parallels, lines of equal latitude, are all small circles (except the equator)

Latitude

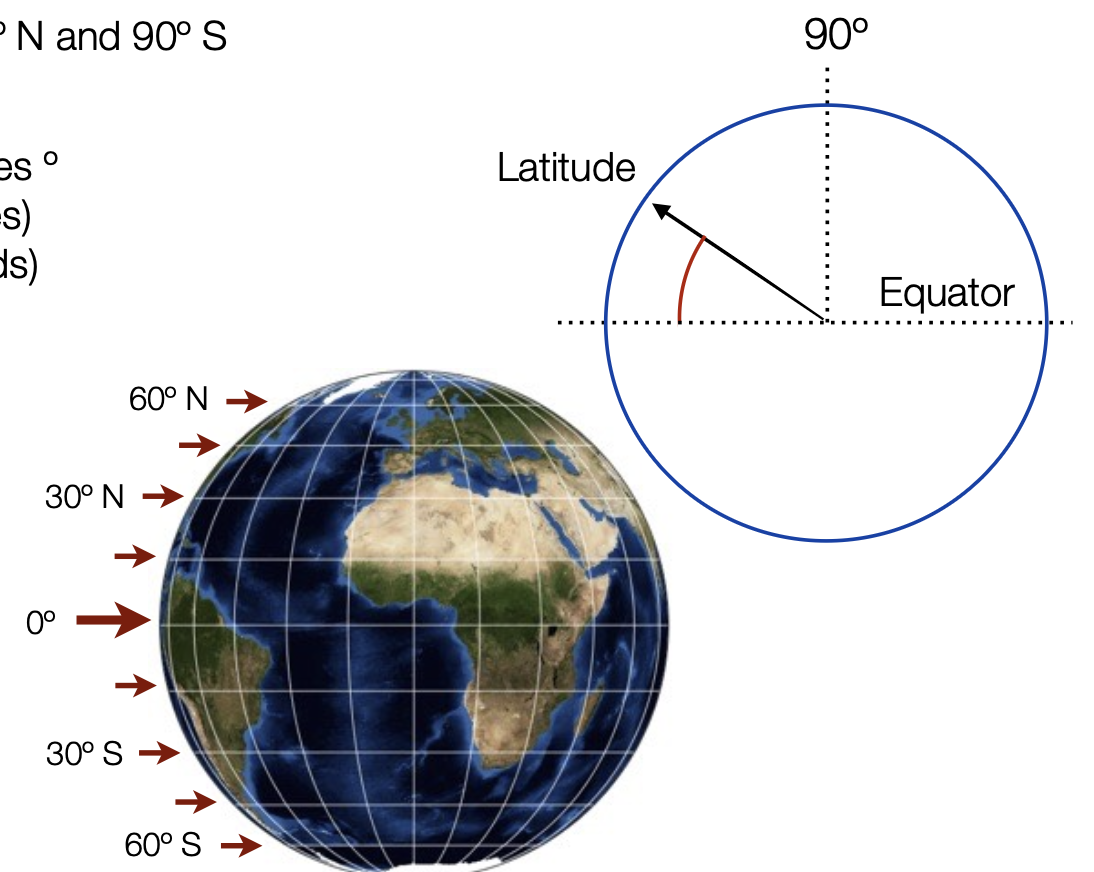
Latitude, or north-south (y)

Angular position between the equator and the North or South Pole, 180 degrees: angle between 90º N and 90º S

 Parallels: lines of constant latitude - Small circles that run east-west, parallel to the equator

How to determine Latitude

In the northern hemisphere, you can find your latitude by measuring the angle between Polaris (the North Star) and the horizon

Historically, a sextant or astrolabe would be used to measure the angle

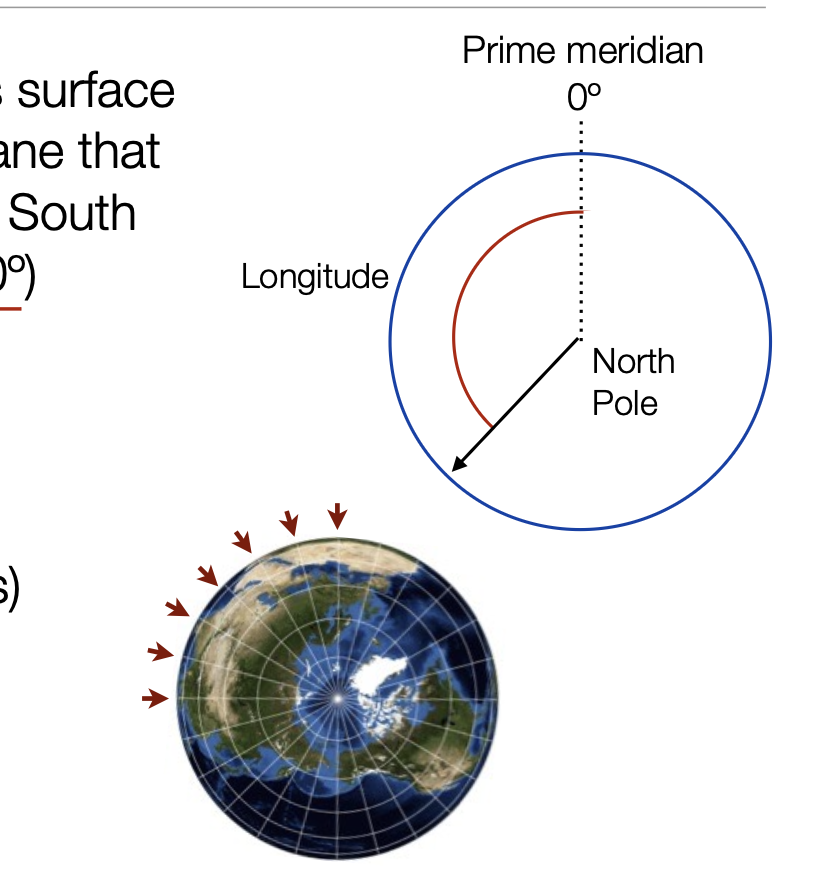
Longitude 

Angular position on the earth’s surface between the intersection of plane that passes through the North and South Pole and the prime meridian (0º)

360 degrees: 180º W to 180 ºE

All lines of longitude (meridians) are great circles

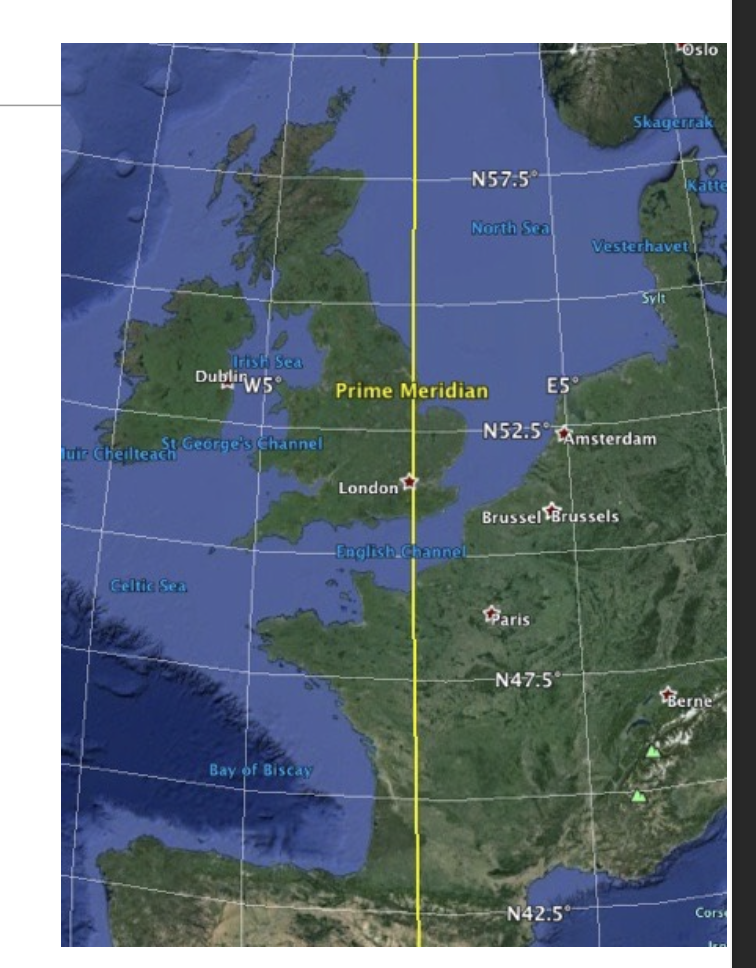
Prime Meridian

Prime meridian is arbitrarily located at the Royal Observatory in Greenwich, UK.

Because the technology for longitude was created in Britain

How to measure Longitude

There was no accurate way to measure longitude until the invention of the marine chronometer, a clock that could keep time at sea.

The Earth spins 15 degrees per hour (360*/24hrs), so (12 noon - current time) x 15*/hr = longitude

If it is 8:00 AM at the prime meridian and noon where you are = 4 hours later than prime meridian x 15º per hour = 60º East longitude

The Graticule 

Web of latitude lines (parallels) and longitude lines (meridians) is called the graticule

- Meridians & parallels always meet at right angles

- Distance between parallels is constant (about 69 mi)

- Distance between meridians varies by latitude (about 69 mi at equator, zero at poles)

- Meridians all intersect at the poles; parallels never intersect

Earth’s true shape:

Oblate spheroid or ellipsoid: the rotation of the earth causes polar flattening due to centrifugal force. This affects distance measurements on maps. 

The truest shape is a geoid, which means the the surface is not smooth, it has “Bumpiness” caused by variations in density of the Earth’s crust (which also causes variabilities in gravity). 

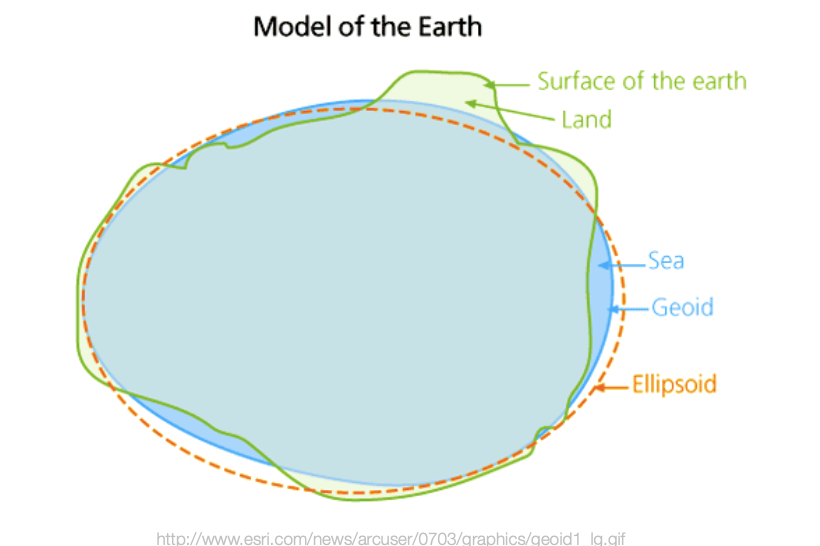
Geodetic Surveys 

Geodetic surveys: detailed measurements of the globe that take into account the curvature and variations in gravity of the Earth. 

Geodetic surveys are used to create a set of points in a control network with very accurate and precise locations

Markers (monuments) are often set up at control points

Horizontal Datums