Number Theory 1 - Prime Numbers and Congruences

State the Division Algorithm

Let a, b ∈ Z with b > 0. Then

there exist unique integers q, r such that a = qb + r and 0 ≤ r < b.

Prove the Division Algorithm

We first show existence. Let S = {a−nb | n ∈ Z}. Then S contains non-negative elements, so contains a least non-negative element, call it r=a−qb. If r≥b then r−b=a−(q+1) b is a smaller non-negative element of S, a contradiction.

We next show uniqueness. If qb+r=ub+s then (q−u)b=s−r. The left-hand side is an integer multiple of b, while the right-hand side satisfies −b < s−r < b. The only possibility is that s = r and q = u.

If r = 0, then a = qb, in which case we say that b divides a and write what?

b|a

Prove that there exists a unique integer d > 0 such that I = dZ = {dn | n ∈ Z}.

I contains positive integers; let d be the least one. Then dZ ⊂ I. If a∈I, we can write a=qd+r with 0≤r<d. If r=/=0 then r∈I, contradicting the minimality of d. Therefore a = qd, showing that dZ = I.

When does there exist x, y ∈ Z with xa + yb = c.

When (a,b)|c.

Why does Euclid’s algorithm have to terminate?

r_k is strictly decreasing

Apply Euclid’s algorithm to a=34, b=25

Result finds 1= -11×34 + 15×25

Define the term prime number

An integer n > 1 is said to be a prime number if the

only integers b > 0 that divide n are b = 1 and b = n.

Prove that if p a prime number, and a, b are integers. If p|ab then p|a or p|b.

Suppose that p does not divide a. Then (a,p) is a positive integer which divides p, so equals 1 or p. It also divides a, so we must have (a, p) = 1 and can write xa+yp = 1 for some x,y ∈ Z. Then b = xab+ypb is divisible by p.

State the Fundamental Theorem of Arithmetic

Every integer n > 0 can be written as a product of primes, in a unique way (up to re-ordering of factors).

Prove the Fundamental Theorem of Arithmetic

The existence is by induction on n > 0, the empty product giving an expression in the base case n = 1. In general, if n is prime then we’re done. Otherwise, we can write n = ab with 1 < a, b < n and we proceed by induction.

For uniqueness, we again argue by induction, the base case following since a non-trivial product does not represent 1 (as primes are greater than 1, by definition). Suppose that n > 1 and we are given two expressions n = product from i=1 to k of p_i^ai = product from j=1 to l of q_j^bj with ai, bj > 0. Then p_1|n, so p_1|q_j for some j = 1, . . . , l. After relabelling, we can assume that p1 = q1. The uniqueness then follows by the uniqueness for n/p1, which holds by induction.

Define what it means for an algorithm to be polynomial-time.

Definition 1.7. An algorithm with input an integer N > 1 is said to be polynomial-time if there are constants b,c > 0, independent of N, such that it always completes after c(logN)^b “elementary operations” (such as adding or multiplying digits in a fixed base).

Give a proof there are infinitely many primes.

Suppose there were only finitely many prime numbers p1, . . . , pk, and let N = p1...pk +1. Then N > 1 has a prime factor p, which cannot be among p1,...,pk.

Prove the following are equivalent:

(a,N)=1.

There exists b∈Z such that ab≡1 mod N.

a + N Z generates the additive group (Z/N Z, +).

(1)⇔(2):If(a,N)=1 then we can write xa+yN =1. Take b = x. Conversely if ab ≡ 1modN then ab = 1+kN, hence (a,N) = 1.

(2) ⇔ (3) : We know that 1+NZ generates Z/NZ, so a+NZ generates if and only if we can find b > 1 such that (a+NZ)+(a+NZ) + ··· + (a + NZ) (b times) equals 1 + NZ, or equivalently such that ab ≡ 1 mod N.

Prove that if we let G be a cyclic group of order N > 1. Then G contains φ(N) elements of exact order N.

G is isomorphic (as a group) to Z/NZ. An element has exact order N if and only if it generates, so this follows from the 3rd part of Lemma 1.9.

State Euler–Fermat Theorem

If a, N ∈ Z with N > 1 and (a,N)=1 then a^φ(N) ≡1 mod N.

Prove Euler–Fermat Theorem

Let G = (Z/NZ)×. Lagrange’s Theorem implies that each ele- ment of G has order dividing #G = φ(N). Since the group operation is multiplication, this says exactly that for each a ∈ (Z/NZ)×, we have aφ(N) ≡ 1 mod N.

State Fermat’s Little Theorem

If p is a prime number and a∈Z then ap ≡a mod p.

Prove Fermat’s Little Theorem

If p|a then ap and a are both congruent to 0modp. If p ∤ a then (a, p) = 1 so Euler–Fermat gives ap−1 ≡ 1 mod p. The result then follows on multiplying both sides by a.

Solve x ≡ 7 mod 10 and x ≡ 3 mod 13.

x = -153

State the Chinese Remainder Theorem

Let m1, . . . , mk be pos- itive integers which are pairwise coprime (i.e. (mi,mj) = 1 if i ̸= j. Let M = m1 ...mk. Let a1,...,ak ∈ Z. Then there exists a solution x ∈ Z to the system of simultaneous congruences [x ≡ a_1 mod m_1,…, x ≡ a_k mod m_k]

Prove the Chinese Remainder Theorem

We first establish uniqueness. If x, y satisfy (∗) then mi|(x − y) for all i. As no mi,mj have any common prime factors, this implies that M|(x − y) and x ≡ y mod M.

We next establish existence. Let Mi = M/mi = product over j=/ of=i mj. Then (mi,Mi)=1,so we can find ci ∈Z such that ciMi ≡1modmi. We then automatically have ciMi ≡ 0 mod mj for all j ̸= i as mj|Mi in this case.

Then x = Sum from I=1 to k of a_i c_i M_i is a solution.

Prove the following: Let m1, . . . , mk be positive integers that are pairwise coprime, and let M = m1 ...mk. Then the map ceta (see notes) is a ring isomorphism, i.e. a bijective map that preserves multiplication and addition.

Addition and multiplication are defined componentwise, so are preserved by definition. We just need to check that θ is bijective. This is exactly the content of the Chinese Remainder Theorem.

Let m1, . . . , mk be positive integers that are pairwise coprime. Then there is a group isomorphism (Z/MZ)^x ~= (Z/M1Z) x … x (Z/MkZ)

The map θ restricts to a bijection between the sets of elements that admit a multiplicative inverse. The set of such elements in Z/MZ is (Z/MZ)×, by definition. Since multiplication in the target of θ is de- fined componentwise, an element of the target admits a multiplicative inverse if and only if each component does.

Define what it means for a function to be multiplicative.

Let N = {a ∈ Z | a ≥ 1}, and let f : N → C be a function. We say that f is multiplicative if for all m,n ∈ N with (m,n) = 1, we have f(mn) = f(m)f(n). We say that f is totally multiplicative if for all m,n ∈ N, we have f(mn) = f(m)f(n).

Prove φ is multiplicative.

This follows from Corollary 1.15 as φ(m) is the cardinality of (Z/mZ)×, by definition.

Prove if f : N → C is a multiplicative function, then so is g(n) = 􏰊d|n f(d).

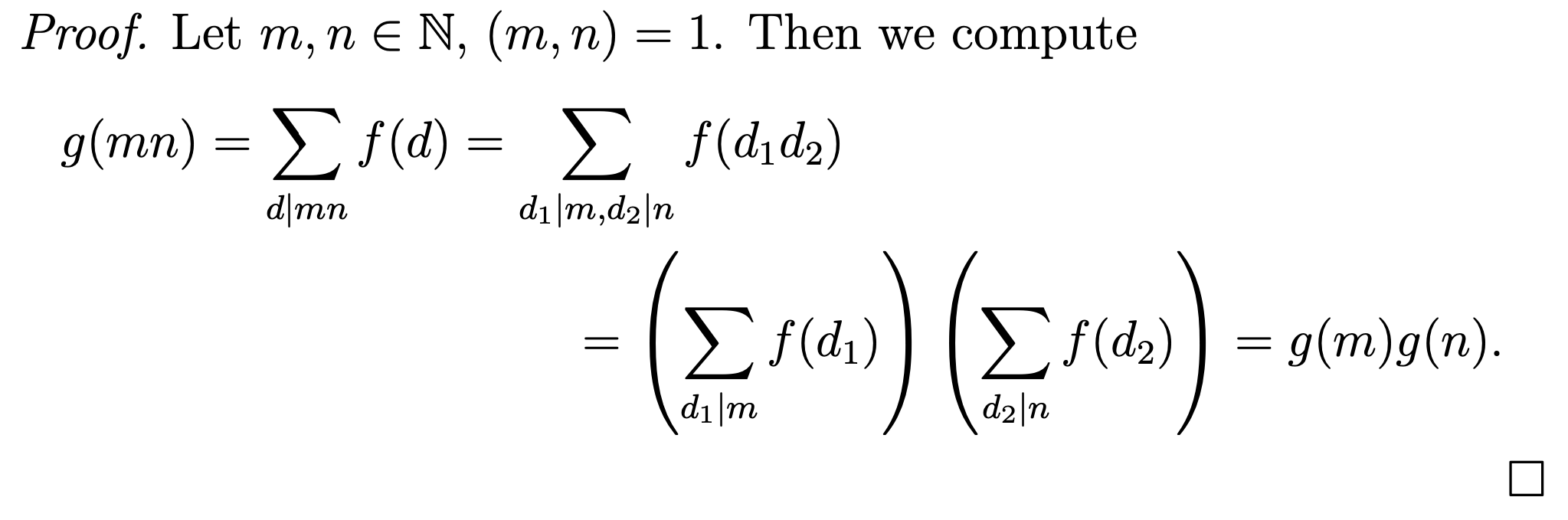
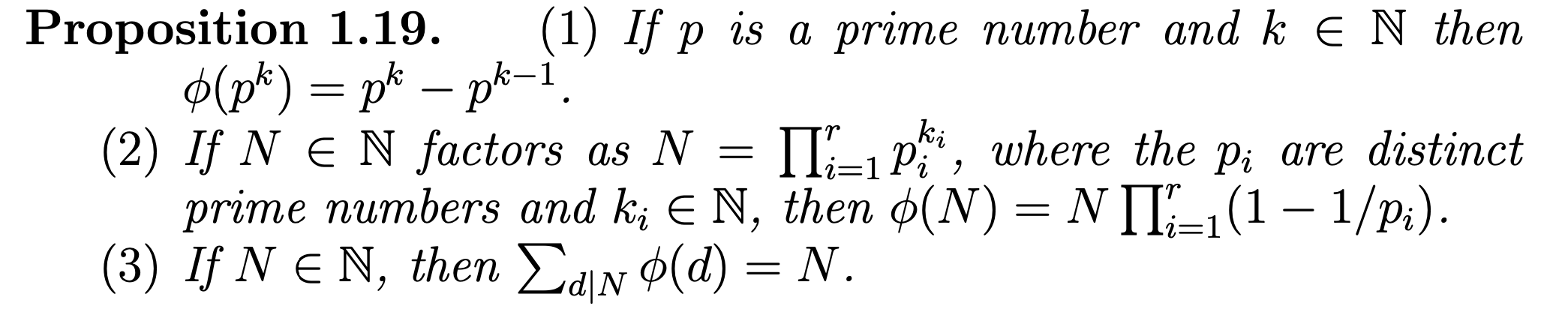
Prove this proposition

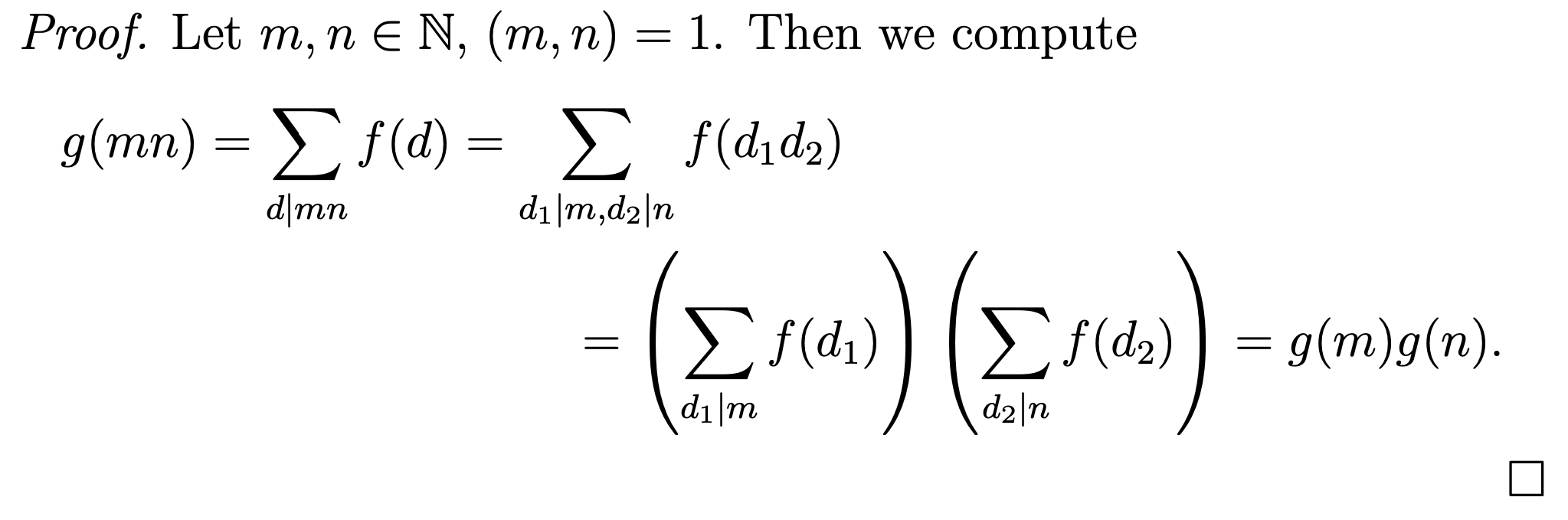
State Lagrange’s Theorem

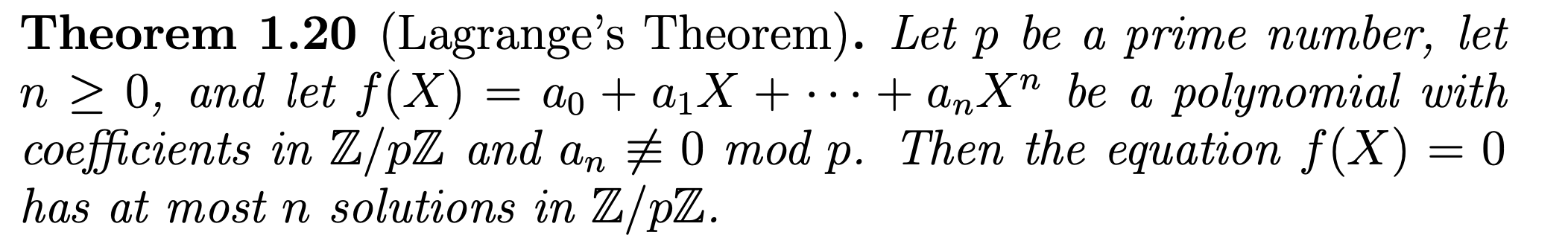
Prove Lagrange’s Theorem

Prove if p is a prime number then the group G = (Z/pZ)×

is cyclic (of order p − 1).

Define the term primitive root.

If p is a prime number and a ∈ Z, we say that a is a primitive root modulo p if (a, p) = 1 and a mod p generates (Z/pZ)×.

Find whether 2 and 3 are primitive roots of 7.

3 is, 2 isn’t

Prove the following:

Let p be an odd prime, let k ∈ N, and let x,y ∈ Z. Then:

(1) If x ≡ 1 + pky mod pk+1, then xp ≡ 1 + pk+1y mod pk+2.

(2) (1 + py)pk ≡ 1 + pk+1y mod pk+2.

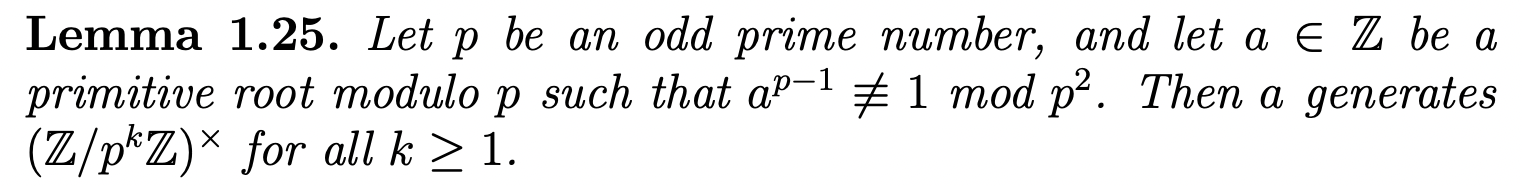
prove this lemma

Prove this theorem